3.2. Математическое описание динамики манипуляционного механизма
Составление математической модели заключается в составлении системы уравнений, с помощью которых осуществляется математическое описание исследуемого объекта. На этом этапе динамического расчета приходится прибегать к упрощениям, принимать некоторые гипотезы и допущения, компенсирующие недостатки знания или упрощающие саму процедуру математического описания динамической модели и ее дальнейший анализ [15, 19, 11, 23]. Здесь также требуется инженерная интуиция, основанная на понимании связи и соответствия математического анализа физическому явлению. Составление математической модели требует знания законов механики и некоторых экспериментальных закономерностей, учитывающих взаимодействие сил и отношение скоростей в процессе передачи энергии от двигателя к звену манипуляционной системы.
В основу наиболее простой динамической модели манипулятора положены следующие допущения и ограничения:
динамическая модель робота с “жесткими” звеньями (пренебрегаем деформацией звеньев и элементов кинематических пар);
звенья манипуляторов (за исключением стойки) рассматривать как тонкие однородные стержни с заданной длиной и массой;
кинематические пары будем рассматривать как идеальные (звенья сочленяются без зазоров);
законы движения звеньев заданы, т.е. в каждый момент времени известны координаты, скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев;
все активные силы (за исключением движущих) считать известными или заданными функциями параметров движения.
Результаты, полученные на основе работы этой модели, принято считать «идеальными». Анализ модели дает исходное оценочное представление о влиянии соотношения скоростей и масс передаточных и исполнительных механизмов, а также соотношения активных и пассивных сил на закон движения ИС проектируемой степени подвижности манипулятора.
Итак, относительное
перемещение i-го
звена относительно связанного с ним
(i-1)-го
звена представляет собой регулируемую
переменную
,
которая должна изменяться с помощью
i-го
привода по желаемому закону. Вектор
является вектором обобщенных координат
манипуляционного механизма. Пренебрегаем
силами трения в кинематических парах
(их можно учесть в КПД кинематических
цепей ИС). Тогда для системы тел,
находящихся в потенциальном поле сил
тяжести, уравнения Лагранжа II
рода записываются в векторной форме:
,
(3.1)
где
вектор обобщенных скоростей,
и
- кинетическая и потенциальная энергия
манипуляционного механизма,
- вектор обобщенных сил, который является
суммой двух векторов
(вектор сил, передаваемых исполняемыми
двигателями звеньям манипулятора через
устройства передачи движения) и
(вектор внешних сил).
.
(3.2)
Для вращательных движений векторы , , понимаются как соответствующие векторы моментов сил.
Кинетическая
энергия манипулятора
связана с вектором обобщенных скоростей
с помощью симметричной
матрицы инерционных характеристик
,
компоненты которой зависят от значений
обобщенных координат:
(3.3)
Вычислив полную производную по времени в выражении (3.1), получим следующее уравнение динамики:
,
(3.4)
где
- вектор статических сил.
Полученное выражение (3.4) можно преобразовать к виду:
,
(3.5)
где
.
В (3.5) вектор
характеризует моменты сил, обусловленные
положениями и скоростями движения
звеньев манипулятора (т.е. центробежных
и кориолисовых сил), а вектор
характеризует моменты, вызванные силами
тяжести движущихся масс элементов
манипулятора. Компоненты этих векторов
зависят от элементов вектора положений
звеньев, а вектор
кроме этого еще и от скоростей движения
звеньев манипулятора. При этом i-ый
компонент векторов может являться
функцией многих составляющих векторов
и
,
а не только величин
и
.
Это свидетельствует о проявлении
динамического взаимодействия звеньев.
Изменение положения одного из звеньев
неминуемо приводит к силовому воздействию
на другие звенья, от чего характер
движения последних искажается.
Для манипуляционного механизма с N степенями подвижности в соответствии с выражением (3.5) система дифференциальных уравнений Лагранжа II рода примет вид
,
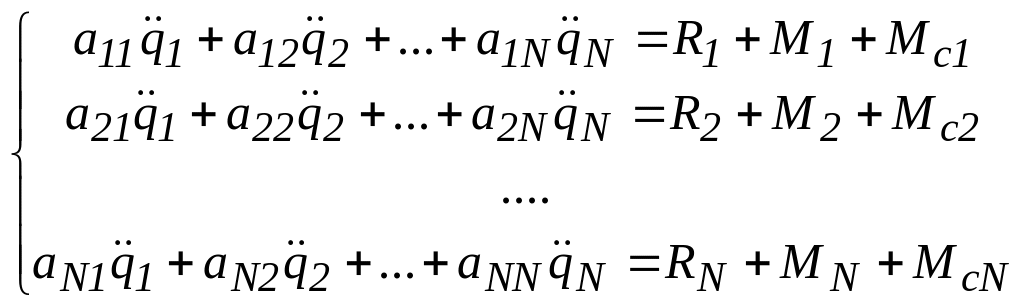(3.6)
где
,
,
…,
– компоненты симметричной матрицы
инерционных характеристик:
.
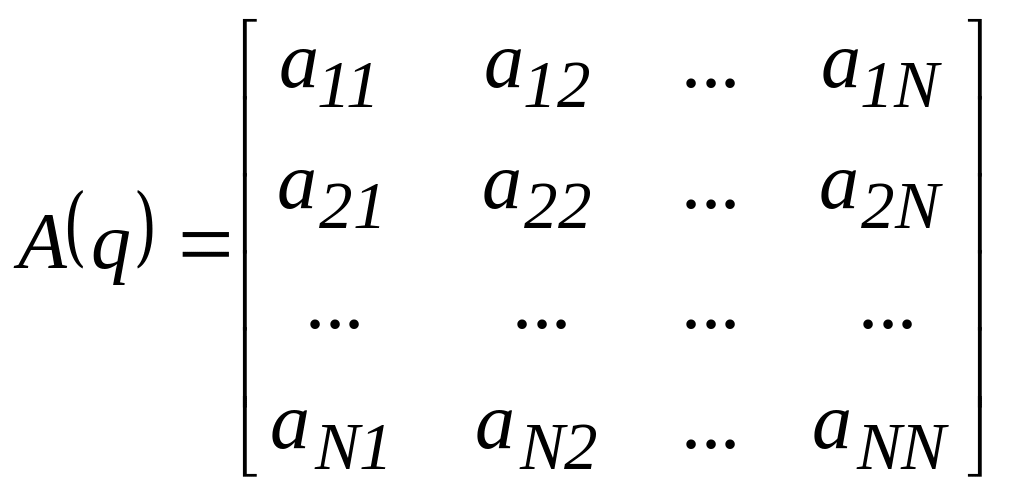(3.7)
В соответствии с вариантом задания необходимо разработать в среде MATLAB динамическую модель манипуляционного механизма. Для определения максимального значения момента статических сил и диапазона значений, которые принимает момент инерции разрабатываемой степени подвижности, следует смоделировать решение обратной задачи динамики, т.е. обобщенные координаты и их производные являются входными сигналами модели [25].
На заключительном же этапе исследования и уточнения параметров разработанной ИС данная динамическая модель манипулятора позволит получить значения обобщенной силы, являющейся возмущающим воздействием цепи формирования скорости ИС.