ФГБОУ ВПО «Воронежский государственный

технический университет»

Кафедра «Теоретическая и прикладная механика»

- 2013

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по выполнению контрольной работы № 1

по разделу «Сопротивление материалов»

дисциплины «Прикладная механика» для студентов

направления 140400.62 «Электроэнергетика и электротехника»

(профиль «Электропривод и автоматика»)

заочной формы обучения

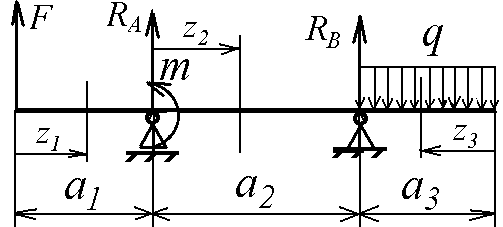
Воронеж 2013

Составители: канд. техн. наук В.А. Рябцев,

канд. техн. наук А.Д. Хван,

ст. преподаватель С.И. Свиридов

УДК 539.317

Методические указания по выполнению контрольной работы № 1 по разделу «Сопротивление материалов» дисциплины «Прикладная механика» для студентов направления 140400.62 «Электроэнергетика и электротехника» (профиль «Электропривод и автоматика») заочной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. В.А. Рябцев, А.Д. Хван, С.И. Свиридов. Воронеж, 2013. 26 с.

Методические указания содержат задания для конт-рольной работы, состоящей из трех задач¸ краткие теорети-ческие справки по тематике задач и примеры решения подобных задач.

Методические указания подготовлены в электронном виде в текстовом редакторе Microsoft Word и содержатся в файле MetSopromat2013.doc.

Ил. 3. Табл. 8. Библиогр.: 2 назв.

Рецензент канд. техн. наук, доц. В.В. Елисеев

Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. Д.В. Хван

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

© ФГБОУ ВПО «Воронежский

государственный технический

университет», 2013

Введение

Основными критериями работоспособности деталей и узлов машин является прочность, жесткость и устойчивость.

Под прочностью понимается способность детали машины выдерживать в процессе эксплуатации заданные рабочие нагрузки без разрушения.

Под жесткостью понимается способность детали машины эксплуатироваться в заданных условиях при деформациях, не превышающих заданные пределы, определенные по условиям эксплуатации.

Под устойчивостью детали машины понимается ее способность сохранять заданную форму равновесия под действием рабочих нагрузок.

В данных методических указаниях рассматриваются три типовые задачи сопротивления материалов по оценке прочности и жесткости брусьев при кручении и изгибе, а также оценке устойчивости сжатого бруса.

Для каждой задачи приведены десять расчетных схем и десять вариантов числовых исходных данных. Номер расчетной схемы выбирается по последней цифре шифра студента. Номер строки числовых исходных данных выбирается по предпоследней цифре указанного шифра. Во всех случаях цифра 0 соответствует числу 10.

Задача № 1 по теме «Расчеты на прочность и жесткость при кручении вала круглого сечения»

Таблица 1.1

1.1. Задание. К стальному ступенчатому валу, имеющему сплошное круглое поперечное сечение, приложены четыре момента. Левый конец вала защемлен в опоре, а правый конец свободен. Собственный вес вала не учитывать.

Требуется:

1. Определить крутящие моменты 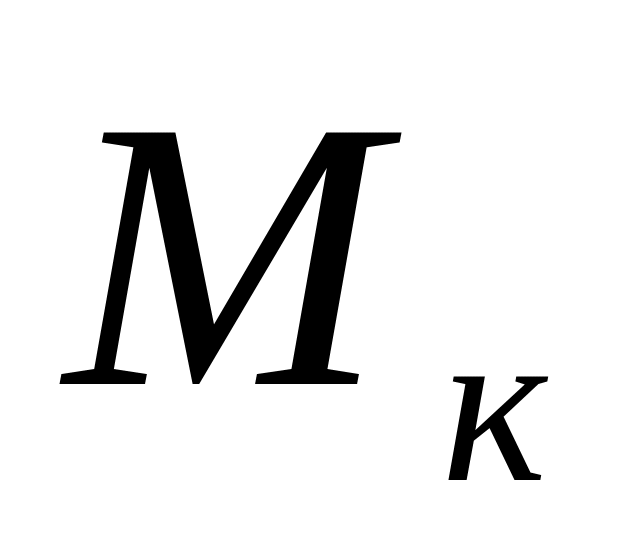в поперечных сечениях вала и построить их эпюру.

2. При заданном значении допускаемого касательного напряжения определить диаметры 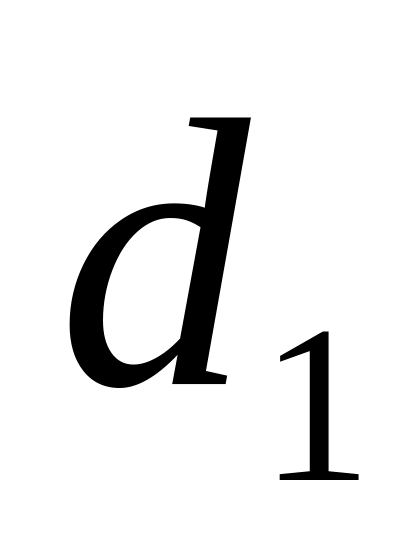и вала из расчета на прочность, полученные значения выразить в миллиметрах и округлить до целых значений из предпочтительного ряда чисел в машиностроении.

3. Построить эпюру максимальных касательных напряжений в сечениях вала

4. Построить эпюру углов закручивания поперечных сечений вала относительно защемленного сечения, приняв модуль сдвига G = 8*10⁴ МПа.

Схему вала выбрать из табл. 1.1, а числовые данные взять из табл. 1.2.

Таблица 1.2

Номер строки	Расстояния, м			Моменты, кН*м				Допускаемое на-пряжение [τ] МПа
	а	b	c	T1	T2	T3	T4
1	0,10	0,14	0,10	5,1	2,1	1,1	0,1	60
2	0,11	0,15	0,11	5,2	2,2	1,2	0,2	60
3	0,12	0,16	0,12	5,3	2,3	1,3	0,3	65
4	0,13	0,14	0,13	5,4	2,4	1,4	0,4	65
5	0,14	0,15	0,14	5,5	2,5	1,5	0,5	50
6	0,15	0,15	0,15	5,6	2,6	1,6	0,6	50
7	0,16	0,17	0,16	5,7	2,7	1,7	0,7	55
8	0,17	0,19	0,17	5,8	2,8	1,8	0,8	55
9	0,18	0,19	0,18	5,9	2,9	1,9	0,9	70
0	0,19	0,20	0,19	6,0	3,0	2,0	1,0	70

1. Теоретическая справка

Кручением стержня называется вид нагружения, при котором в его поперечных сечениях возникает только крутящий момент .

В каждой точке поперечного сечения вала возникает касательное напряжение , определяемое по формуле

, (1.1)

где - расстояние от центра тяжести сечения до рассматриваемой точки сечения; - полярный момент инерции поперечного сечения.

Максимальное касательное напряжение возникает в точках поперечного сечения, для которых . Оно определяется по формуле

1.2)

где - полярный момент сопротивления поперечного сечения вала.

Для круглого поперечного сечения с диаметром

, (1.3)

При кручении вала в пределах выполнимости закона Гука каждое поперечное сечение (кроме жёстко закреплённого сечения) поворачивается, как целое, на некоторый угол относительно продольной оси и остается плоским. При этом расстояния между поперечными сечениями не изменяются.

Взаимный угол поворота двух поперечных сечений, отстоящих на расстоянии , определяется по формуле

(1.4)

где - модуль сдвига материала; - дифференциал координаты вдоль оси вала.

1.3. Пример решения задачи

Рассмотрим стальной ступенчатый вал (рис. 1.1 а); имеющий круглое поперечное сечение и нагруженный четырьмя моментами , , , .

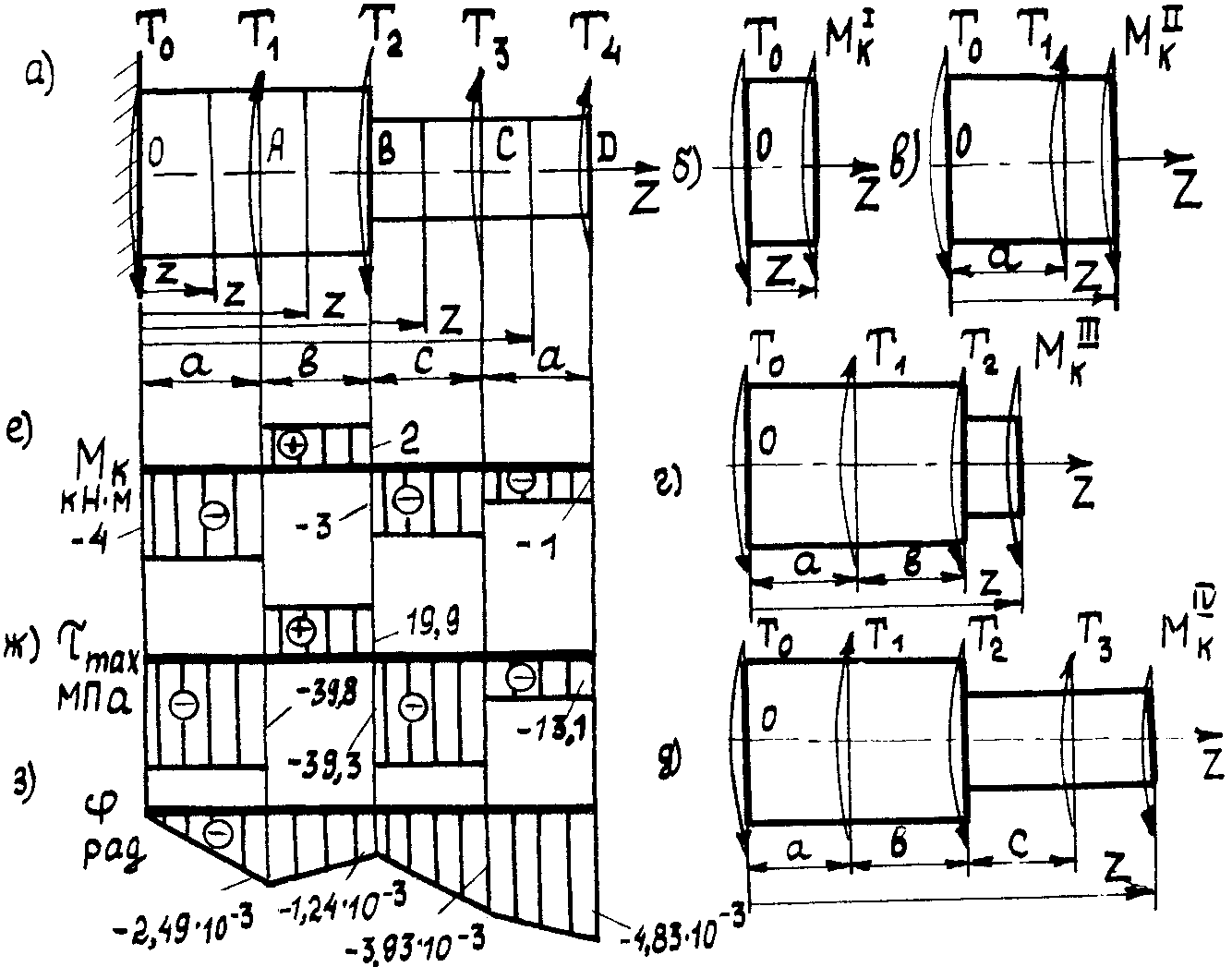
Рис. 1.1

Левый конец вала жестко защемлен в опоре, а правый конец свободен. Допускаемое касательное напряжение , модуль сдвига материала вала , расстояния .

Подобные задачи решаются в следующем порядке.

а) Определение момента в опоре.

Опорный момент определим из уравнения равновесия моментов, приложенных к валу, относительно оси

, .

В итоге имеем: .

б) Построение эпюры крутящих моментов по длине вала.

Вал имеет четыре участка. Крутящий момент в поперечных сечениях вала определяем методом сечений. При этом следует рассматривать все участки вала.

1 участок,

.

Рассечём мысленно вал на две части поперечным сечением, отстоящем на расстоянии от левого конца (рис. 1.1 б), отбросим правую часть вала и её действие на левую часть вала заменим крутящим моментом , направленным против хода часовой стрелки при взгляде на сечение со стороны внешней нормали к сечению. Составим уравнение равновесия для оставшейся левой части вала, а именно, приравняем нулю сумму моментов относительно оси :

, , .

Рассуждая аналогично, получим

2 участок, , рис. 1.1, в

, , .

3 участок, , рис. 1.1, г

, ,

.

4 участок, , рис. 1.1, д

, ,

.

Таким образом, на каждом из участков крутящие моменты постоянны. Эпюра крутящих моментов приведена на рис. 1.1 е

в) Определение диаметров , вала из расчёта на прочность.

Расчёт на прочность проводится по схеме

, отсюда .

На участке бруса имеем

, .

На участке вала имеем

, ,

.

г) Построим эпюру максимальных касательных напряжений по длине вала.

На 1 участке

.

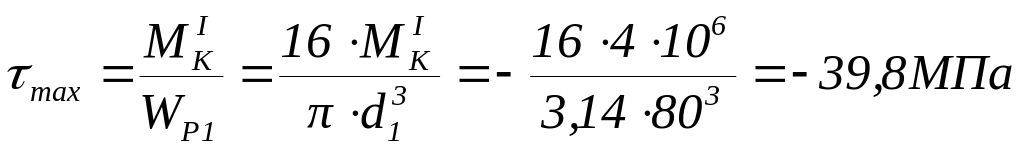На 2 участке

.

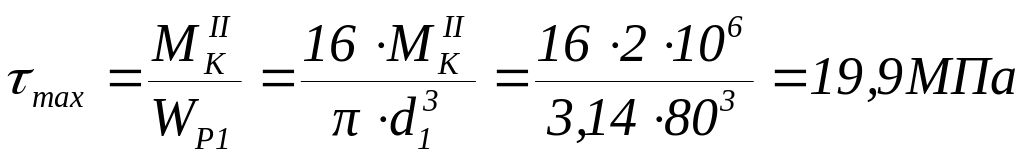На 3 участке

.

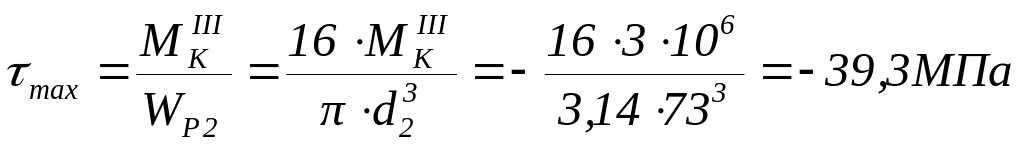На 4 участке

.

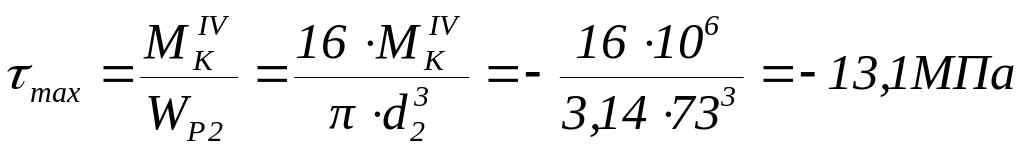Эпюра напряжений приведена на рис. 1.1 ж

г) Построение эпюры углов взаимного поворота сечений (углов закручивания) .

Так как на каждом из четырёх участков вала величины , , постоянны, то из формулы (1.4) следует; что угол линейно меняется по длине вала. Угол поворота левого (закреплённого) поперечного сечения вала равен нулю; а углы поворота:

сечения относительно сечения -

сечения относительно сечения -

сечения относительно сечения -

сечения относительно сечения -

соответственно равны:

.

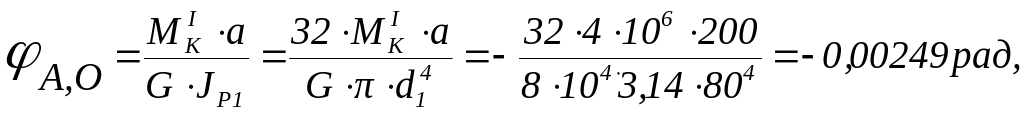
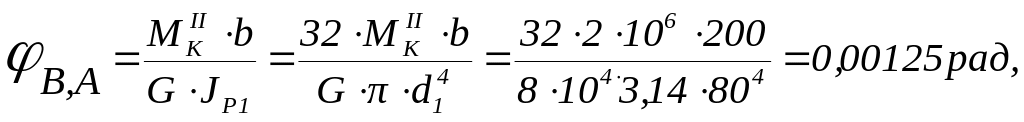
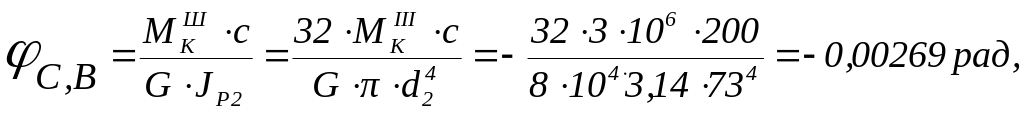
Тогда углы поворота сечений В, С, относительно закрепленного сечения О соответственно, равны

-0,00124 рад,

-0,00393 рад,

-0,00483 рад.

Эпюра углов поворота сечений вала приведена на рис. 1.1 з.

Задача № 2 по теме

«Расчет на прочность при изгибе балки»

2.1 Задание. Для заданной схемы стальной балки (табл. 2.2) требуется построить эпюры поперечных сил и изгибающих моментов, определить максимальный изгибающий момента , и подобрать номер двутаврового поперечного сечения из расчета на прочность, если допускаемое нормальное напряжение равно = 150 МПа. Числовые данные взять из табл. 2.1. Собственный вес балки не учитывать. Значения моментов сопротивления сечений при изгибе для нескольких номеров двутавровых сечений (ГОСТ 8239-72) приведены в табл. 2.3.

Таблица 2.1

Номер строки	а, м	b, м	с, м	l, м	Момент М, кН·м	Сосредо-точенная сила F, кН	Равно- мерно распределен-ная нагрузка q, кН/м
1	2.0	3.2	1.8	10	7	20	22
2	2.2	3.4	1.9	10	7	19	21
3	2.4	3.6	2.0	11	8	18	20
4	2.6	3.8	2.1	11	8	16	19
5	2.8	4.0	2.2	12	9	15	18
6	3.0	4.2	2.3	12	9	14	17
7	3.2	4.4	2.4	13	10	13	16
8	3.4	4.6	2.5	13	10	12	15
9	3.6	4.8	2.6	14	11	11	14
0	3.8	5.0	2.7	14	11	10	13

Таблица 2.2

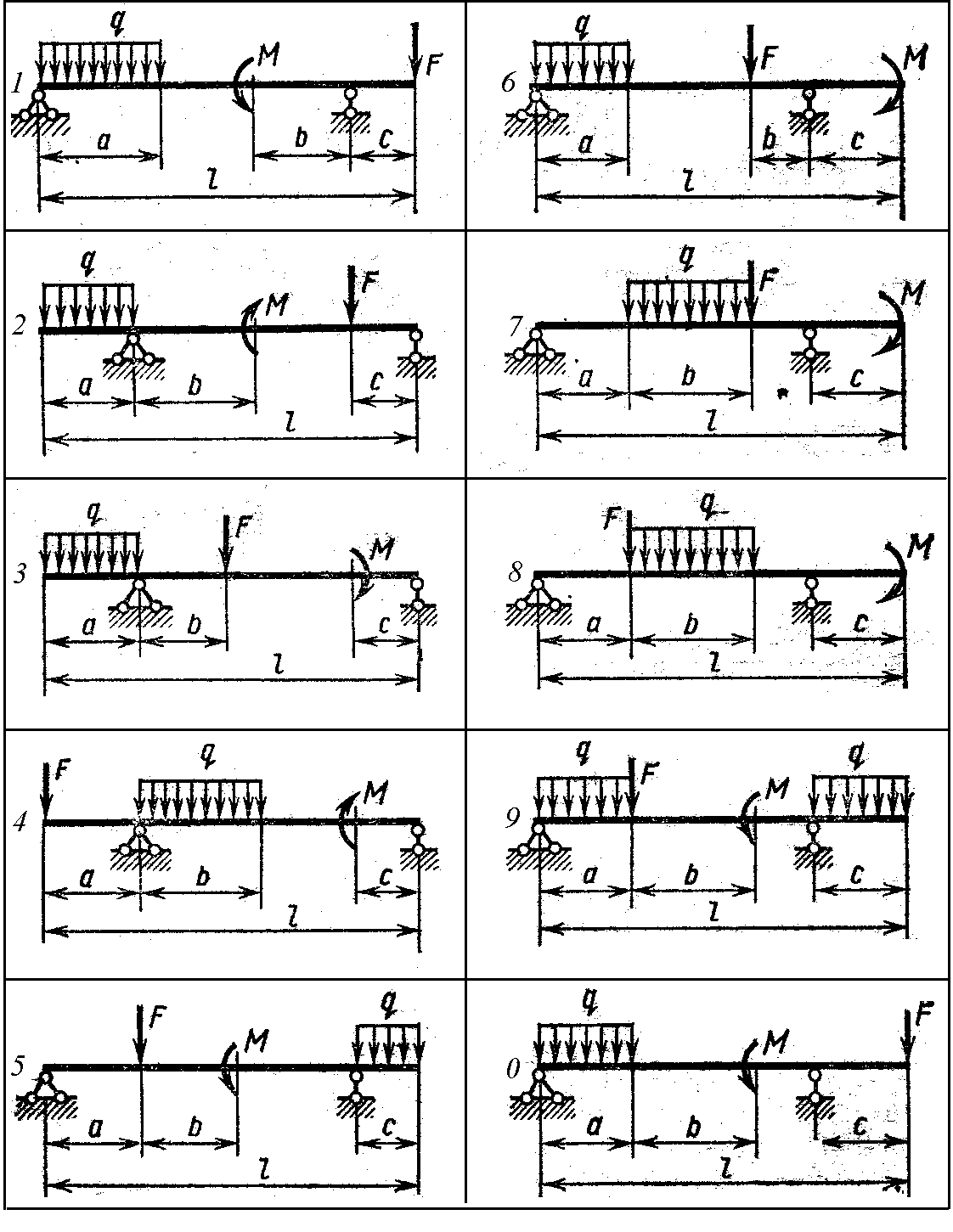
Таблица 2.3

Номер двутавра	10	12	14	16	18	18а	20	20а
Wx , см3	39,7	58,4	81,7	109	143	159	184	203
Номер двутавра	22	22а	24	24а	27	27а	30	30а
Wx, см3	232	254	289	317	371	407	472	518