
- •Оглавление
- •Введение
- •1. Конструкция автомобильных кранов
- •1.1. История развития автомобильных кранов в России
- •1.2. Конструкция современных автомобильных кранов
- •1.2.1. Коробки отбора мощности
- •1.2.2. Опорные рамы
- •1.2.3. Выносные опоры
- •1.2.4. Механизм блокировки
- •1.2.5. Опорно-поворотные устройства (опу)
- •1.2.7. Кабина крановщика
- •1.2.8. Стреловое оборудование
- •1.2.9. Крюковая обойма
- •1.3. Механизмы кранов
- •1.3.1. Механизм подъема груза
- •1.3.2. Механизм поворота
- •1.4. Гидропривод автомобильных кранов
- •1.4.1. Общая характеристика гидропривода автокранов
- •Гидравлические схемы привода кранов
- •1.4.3. Устройство и назначение элементов гидроприводов
- •1.4.4. Аппараты управления гидроприводами
- •2. Общий расчет автомобильного крана
- •2.1. Разработка расчетной геометрической схемы автокрана
- •2.1.1. Выбор базового автомобиля.
- •2.1.2. Определение масс узлов автокрана
- •2.1.3. Определение геометрических параметров крановой установки
- •2.1.4. Определение координат центра тяжести крана
- •2.2. Проверка устойчивости крана от опрокидывания
- •2.2.1. Проверка устойчивости крана при испытательных нагрузках
- •2.2.2. Проверка устойчивости крана при номинальных нагрузках
- •2.2.3. Построение грузовысотной характеристики автокрана
- •3. Расчет механизмов крана
- •3.1. Механизм подъема груза
- •3.1.1. Исходные данные для расчета механизма подъема груза
- •3.1.2. Определение режима работы крана
- •3.1.3. Выбор параметров полиспаста
- •3.1.4. Выбор грузоподъемного каната
- •3.1.5. Расчет крюковой подвески
- •3.1.6. Определение параметров барабана
- •3.1.7. Определение потребной мощности лебедки
- •3.1.8. Выбор редуктора
- •3.1.9. Стали для зубчатых колес
- •3.1.10. Выбор муфты
- •3.1.11. Выбор тормоза
- •3.1.12. Компоновка грузоподъемного механизма
- •3.1.13. Компоновка опорной рамы лебедки
- •3.2. Расчет механизма поворота
- •3.2.1. Кинематические схемы механизмов поворота
- •3.2.2. Исходные данные для расчета механизма поворота
- •3.2.3. Определение моментов сил сопротивления повороту
- •3.3. Расчет деталей механизма поворота
- •3.4. Расчет механизма наклона стрелы
- •3.5. Расчет механизма телескопирования стрелы
- •3.6. Расчет параметров гидрообъемных передач
- •4. Расчет элементов металлоконструкции автокрана
- •4.1. Расчет балок выносных опор
- •4.1.1. Определение опорных нагрузок
- •4.2. Расчет телескопической стрелы
- •5. Правила безопасной эксплуатации автомобильных кранов
- •Контрольные вопросы и задания
- •Заключение
- •Библиографический список рекомендуемой литературы
- •Определение нагрузок и центра тяжести крана
- •3 94006 Воронеж, ул. 20-летия Октября, 84
3.1.7. Определение потребной мощности лебедки
Статическая потребная мощность для подъема номинального груза массой Q(т) cо скоростью Vгр (м/с) может быть подсчитана по формуле
![]() ,
(2.25)
,
(2.25)
где g – ускорение свободного падения, g = 9,81 м/с;
ηп – КПД полиспаста, определяемый в зависимости от кратности полиспаста и КПД входящих в него блоков η по формуле
![]() .
(3.26)
.
(3.26)
Среднее значение КПД блока на подшипниках качения при угле охвата его канатом 180° принимают равным η ≈ 0,98.
КПД редуктора зависит от типа редуктора и количества ступеней. КПД одной цилиндрической зубчатой пары в масляной ванне с валами на подшипниках качения принимают ηцп = 0,98; КПД конической зубчатой пары при работе в аналогичных условиях принимают ηкп = 0,97; червячная пара при однозаходном червяке имеет КПД ηчп = 0,74.
КПД двухступенчатого редуктора с цилиндрическими зубчатыми колесами в проектных расчетах можно принимать равным ηр = ηцп2 = 0,96. Аналогично определяют КПД редукторов с различной комбинацией типов передач.
Статическую мощность двигателя корректируют коэффициентом Кр, который учитывает назначение крана, режим работы механизма, вид управляющего устройства. Механизмы подъема автомобильных кранов можно отнести к группе механизмов с режимом работы М2 – М5 и числом включений в час не менее 60 – 150. Для этих условий – Кр= 1,25.
С учетом сказанного мощность двигателя рассчитывают по формуле
Nэ = Nc / Кр. (3.27)
При выборе гидравлического двигателя необходимо задаться номинальным давлением в гидросистеме – рном . Современные гидравлические краны работают при давлении жидкости в гидросистеме рном= 20…25 МПа и частоте вращения вала пдв = 40…20 с-1. Расчетным параметром для выбора гидродвигателя служит номинальный рабочий объем q. Его определяют по формуле
q = 2π∙Mдв / Δp∙ηм , (3.28)
где Мдв = Nэ/ωдв – эквивалентный момент на валу двигателя;
ωдв = π∙ пдв , с-1 – номинальная угловая скорость вала двигателя;
Δр ≈ 0,85рном – вероятная величина перепада давления в гидросистеме;
ηм – механический КПД гидромотора.
3.1.8. Выбор редуктора
Рациональный подход к проектированию механизмов заключается в максимально возможном использовании стандартных или серийно выпускаемых элементов, узлов, агрегатов. В [д.9] приведены технические данные серийно выпускаемых редукторов с цилиндрическими колесами. Для выбора редуктора можно использовать и другие источники. При выборе редуктора учитываются следующие факторы:
- относительное расположение входных и выходных валов, оговоренных исполнением редуктора;
- передаточное число iр;
- допустимые нагрузки на выходной вал: крутящий момент Мт, радиальная сила Fр;
- номинальная частота вращения входного (быстроходного) вала nдв;
- габаритные размеры корпуса редуктора L × В × Н, мм;
- коэффициент полезного действия ηр;
- уровень шума;
- относительная стоимость, руб./ Н·м.
Требуемое передаточное число редуктора iр определяют по формуле
iр = nдв / nб. (3.29)
Крутящий момент на тихоходном валу вычисляют из условия действия усилия, приложенного к барабану грузоподъемным канатом при подъеме испытательного груза:
Мтр =[1,25Fф (Dб + dк ) /2] Креж , кН·м, (3.30)
Креж – коэффициент режима работы: Креж = Кдв Кпв Кс Км Крев;
Кдв – коэффициент, зависящий от вида двигателя. Для гидродвигателей Кдв= 1; Для строительных кранов Кс = 1,0; Км учитывает характер работы приводимой машины. Работа грузоподъемных кранов характеризуются умеренными толчками. Км = 1,2. Кпв – коэффициент, зависящий от продолжительности включения (табл. 3.3). Для механизма подъема коэффициент реверсирования Крев= 1,0.
Таблица 3.3
Значения Кпв при продолжительности включения привода ПВ, %
-
ПВ,%
100
60
40
25
15
Кпв
1,00
0,90
0,80
0,70
0,67
Выбранный типоразмер редуктора с цилиндрическими колесами обозначают по следующей форме, например: «Редуктор Ц2-350-31,5-11КвхМ». Это означает: редуктор с цилиндрическими колесами, двухступенчатый, межосевое расстояние входного и выходного валов 350 мм, передаточное число 31,5, вариант сборки 11, с коническим быстроходным валом и выходным валом под зубчатую муфту.
Передаточное число iрс выбранного серийного редуктора часто точно не совпадает с требуемым iрт . В этом случае корректируют диаметр барабана с точностью ± 5 мм для обеспечения заданной скорости подъема груза по формуле
![]() ,
(3.31)
,
(3.31)
где фактическая частота вращения барабана nбф = nдв / iрс .
П рименение
унифицированных узлов в проектируемых
машинах не всегда позволяет получить
конструкцию, в полной мере отвечающую
технологическим, эксплуатационным,
эргономическим и дизайнерским требованиям
рынка грузоподъемной техники. Применение
в трансмиссии грузоподъемных лебедок
специальных дифференциальных вставок
или встроенных в канатный барабан
планетарных редукторов позволяет
значительно улучшить потребительские
свойства таких агрегатов. Ранее (рис.
3.32 – 3.34) были показаны конструкции
планетарных редукторов, применяемых в
грузоподъемных лебедках. Определение
передаточных чисел и угловых скоростей
выходных звеньев в этих конструкция
будет показано ниже.
рименение
унифицированных узлов в проектируемых
машинах не всегда позволяет получить
конструкцию, в полной мере отвечающую
технологическим, эксплуатационным,
эргономическим и дизайнерским требованиям
рынка грузоподъемной техники. Применение
в трансмиссии грузоподъемных лебедок
специальных дифференциальных вставок
или встроенных в канатный барабан
планетарных редукторов позволяет
значительно улучшить потребительские
свойства таких агрегатов. Ранее (рис.
3.32 – 3.34) были показаны конструкции
планетарных редукторов, применяемых в
грузоподъемных лебедках. Определение
передаточных чисел и угловых скоростей
выходных звеньев в этих конструкция
будет показано ниже.
Использование канатного барабана как корпуса редуктора позволяет получить очень компактную грузоподъемную лебедку. Применение планетарного редуктора для такого конструктивного исполнения лебедки является весьма целесообразным для повышения долговечности и надежности работы грузоподъемного механизма.
П
Рис. 3.8. Схема
планетарного
редуктора
с двумя тормозами
В первом случае номинальную угловую скорость барабана лебедки можно вычислить по формуле
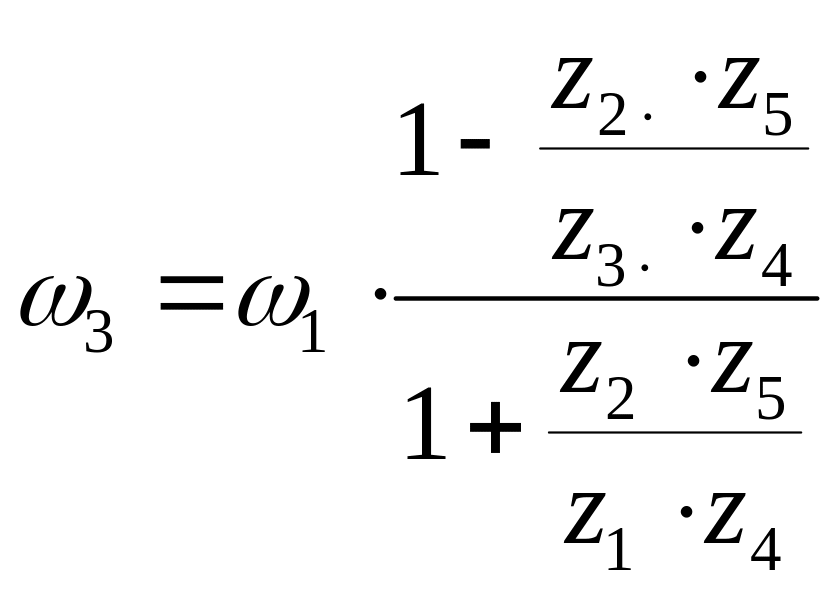 . (3.32)
. (3.32)
Во втором случае номинальную угловую скорость барабана рассчитывают по формуле

 . (3.33)
. (3.33)
Н
Рис. 3.9.
Кинематическая схема дифференциального
механизма
Первый механизм является дифференциальной передачей, состоящей из ведущего центрального колеса z1, сателлита z2, размещенного на водиле Н, и центрального колеса с внутренним зацеплением z3.
Второй механизм представляет собой простой редуктор, состоящий из центрального колеса z4, промежуточного колеса z5 с неподвижной осью и центрального колеса z6. Передаточное число такого редуктора будет
i4-6 = - z6 / z4. (3.34)
Передача движения от первого механизма на второй осуществляется водилом Н на колесо z4. Вследствие чего ωн = ω4. При этом водило Н и центральное зубчатое колесо z3 замкнуты через зубчатую передачу z4, z5, z6, поскольку ω3 = ω6. Передаточное число первого механизма с учетом вышесказанного и при остановленном водиле Н можно вычислить по формуле
i1-3 = i1-3 (1 – iн-3) + iн-3. (3.35)
Полное передаточное число всего механизма соответственно получим
ip
= i1-6 =![]() .
(3.36)
.
(3.36)
Из полученного следует, что направление вращения выходного звена z3 - z6, которое едино с барабаном лебедки, всегда противоположно направлению вращения входному звену z1.
При проектировании лебедок со встроенным планетарным редуктором необходимо решать задачи по определению количества зубьев на колесах, модуля зубьев и, как следствие, диаметров колес, позволяющих вписать планетарный редуктор внутрь грузоподъемного барабана, обеспечив при этом прочность зубьев колес по изгибным и контактным напряжениям.
Для примера воспользуемся редуктором, кинематическая схема которого показана на рис. 3.9. Такой редуктор имеет высокий КПД и часто применяется в различных машинах с диапазоном передаточных чисел 10…60. Порядок решения поставленных задач может быть следующим.
Из предыдущего расчета грузоподъемной лебедки потребуются следующие параметры: диаметр барабана Dб, окружное усилие на барабане Fф, частота вращения барабана nб, частота вращения вала двигателя nдв. При этом для реализации окружного усилия на барабане должен действовать вращающий момент
Мб = Fф · Dб / 2 . (3.37)
Требуемое передаточное число редуктора будет
iр = nдв / nб . (3.38)
Для удобного конструктивного исполнения редуктора и упрощения кинематических расчетов можно принять одинаковым соотношение чисел зубьев колес дифференциальной z3/z1 и замыкающей z6/z4 частей. Обозначив кинематические соотношения
z3/z1 = z6/z4 = х,
выражение (3.36) можно записать в виде квадратного уравнения
х2 + 2х + iр = 0.
Решением этого уравнения будет выражение
![]() (3.39)
(3.39)
Подставив в формулу (3.39) требуемое значение передаточного числа редуктора iр по формуле (3.38), получим передаточные отношения дифференциальной и замыкающей ступеней редуктора.
Количество зубьев на колесах замыкающей ступени редуктора определяем при следующих условиях. Для исключения подрезания зубьев колес принимаем минимальное число зубьев колес z1мин= z4мин= 17 для получения наименьших размеров редуктора с целью его размещения внутри барабана лебедки. Тогда
z3 = z6 = х · z4 мин.
При этом должно быть выполнено условие: z3 – z1 = z6 – z4 – должно быть четным числом. Если условие не выполняется, количество зубьев колес z6 следует уменьшить на 1. На изменение общего передаточного числа редуктора это существенно не повлияет.
Для обеспечения эффективной работы планетарной передачи без значительного ее усложнения обычно принимают число сателлитов с, равное 3. Чтобы обеспечить принципиальную возможность работы и изготовления планетарной передачи, ее необходимо проверить по условиям соседства сателлитов, соосности и сборки.
По условиям соосности центральных зубчатых колес число зубьев сателлитов z2 и z5 должно быть четным:
![]() ;
;
![]() . (3.40)
. (3.40)
Условие соседства сателлитов гарантируется выполнением неравенства
![]() (3.41)
(3.41)
Условие сборки передачи проверяют отношением
![]() (3.42)
(3.42)
где полученное ζ – обязательно должно быть целым числом.
Если вышеуказанные условия не выполняются, то производят корректировку количества зубьев на зубчатых колесах z4, z5, z6 . Аналогичная коррекция должна быть проведена и для первой ступени редуктора после того, как будут определены геометрические размеры выходной ступени. Геометрические размеры зубчатых колес определяют расчетом на выносливость рабочих поверхностей зубьев по контактным напряжениям. Вращающие моменты на зубчатых колесах с учетом ранее принятых кинематических соотношений вычисляют по формулам:
на центральном колесе z1 – М1 = Мб / iр;
на центральном колесе замыкающей ступени z4 – М4 = М1 (z3/z1 + 1);
на колесе z3 – М3 = М1 · z3/z1 ;
на колесе z6 – М6 = М1 · z6/z4 · (z3/z1 + 1).
Чтобы предварительно определить размер наибольшего колеса редуктора (в рассматриваемом варианте кинематической схемы - колесо z6), необходимо задать для него марку стали, способ упрочнения и знать при этом получаемые прочностные характеристики.
