5.7. Геометрическое представление булевых функций
Обозначим
через
множество всех наборов
,
состоящих из чисел
ноль и единица. Множество
называется п-мерным
кубом, а набор
-
вершинами
куба.
Пусть
-
фиксированный набор чисел из 0 и 1.
Множество всех вершин
куба
Е
таких, что
,
,…,
,
1<i
<i
<…<i
,
называется
(п-r)-мерной
гранью. Очевидно,
что (n-r)-мерная
грань является
(n-r)-подкубом
куба Е
.
Например, в трехмерном кубе Е3 наборы (0, 0, 1) и (0, 0, 0) образуют одномерную ( n=3, r=2) грань ( ребро), а наборы (1, 0, 0), (1, 0, 1), (1, 1, 0), (1,1, 1) - двухмерную грань.
Пусть
f(
)
—
произвольная булева функция. Ей
сопоставляется
в соответствие подмножество
вершин куба Е
,
таких что
тогда и только тогда, когда f
=l.
Очевидно, что по подмножеству
исходная функция f(
)
восстанавливается однозначно.
Таким образом, геометрический способ
задания булевой функции
заключается в задании множества вершин
п-мерного
куба Е
,
в которых данная функция истинна.
Пример.
Пусть функция f(
)
задана таблицей истинности. Составить
для нее
множество
.
x |
y |
z |
f( ) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Очевидно, что
Nf={(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0)(1,1,1)}. Множество можно изобразить следующим образом. Рассмотреть вершины трехмерного куба (или просто куба), каждой вершине поставить в соответствие набор из нулей и единиц. Для этого одну из вершин поместить в начало декартовой системы координат, при этом три вершины должны оказаться на координатных осях. Считая, что ребро куба равно единице, каждой вершине поставим в соответствие набор из нулей и единиц, соответствующий координатам вершины в декартовой системе. Для наглядного изображения геометрического представления булевой функции выделяют вершины куба, в которой функция принимает значение 1. На рис. 5.1 изображено геометрическое представление рассмотренной булевой функции.
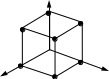Z
(0,0,1)
(0,1,1)
(1,0,1)
(1,1,1)
(0,0,0)
(1,0,0) (0,1,0 )
Y
X (1,1,0)
Рис. 5.1. Геометрическое представление булевой функции
Для
любой булевой функции существует ее
представление
в СДНФ. Причем в алгоритме построения
СДНФ используются
только те наборы значений, при которых
функция равна единице.
Это позволяет проинтерпретировать
геометрическое представление функции
следующим образом. Рассмотрим, например,
ребро куба, представленное вершинами
(1,0,0) и (1,0,1), им соответствуют элементарные
конъюнкции
и
.
Ребру (одномерному подкубу) соответствует
формула
.
Аналогично можно получить формулы, описывающие грани (двумерные подкубы). Например, описанию грани куба, представленной вершинами (1,0,0), (1,0,1), (1,1,0) и (1,1,1), соответствует формула . Описанию грани куба, представленной вершинами (0,0,0), (0,0,1), (0,1,0) и (0,1,1), соответствует формула .
Замечание. Для функций, зависящих от четырёх и более переменных, геометрическое представление применяется очень редко, т.к. трудно построить наглядную модель n - мерного куба при n>3.
Перейдем теперь к геометрической постановке задачи минимизации булевых функций.