1.2. Операции над множествами и их свойства. Диаграммы Эйлера-Венна
Для получения новых множеств из уже существующих используют операции над множествами. Рассмотрим основные из них.
Объединением
множеств X и Y называется
множество
,
все элементы которого являются элементами
множества X или Y:
={x
x
или
}.
Пересечением
множеств X и Y называется
множество
,
элементы которого являются элементами
обоих множеств X и Y:
={x
| x
X
и x
Y}.
Очевидно, что выполняются включения
;
Разностью
множеств X и Y
называется множество
всех тех элементов X, которые не
принадлежат Y:
={x
x
и
}.
Дополнением
множества X называется множество
всех тех элементов x, которые не
принадлежат множеству X:
.
Симметрической разностью (или кольцевой суммой) множеств X и Y называется множество
.
Замечание.
.
Универсальное множество графически изображают в виде множества точек прямоугольника, отдельные области внутри этого прямоугольника соответствуют различным подмножествам универсального множества. Такое представление универсального множества и его подмножеств называется диаграммой Эйлера-Венна. На диаграмме Эйлера-Венна можно проиллюстрировать все основные операции над множествами (рис. 1.1-1.5).
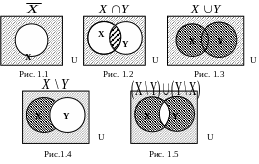
Операции над множествами обладают определенными свойствами и удовлетворяют некоторым соотношениям. Рассмотрим следующие утверждения.
Утверждение 1.2.1. Для любых множеств X, Y, Z выполняются следующие тождества (основные свойства операций):
1. Коммутативность
операций
и
:
2. Ассоциативность операций и :
3. Законы дистрибутивности
4.
.
5.
.
6. Законы
комплиментарности:
7. Законы
идемпотентности:
8. Законы де Моргана:
.
(Август де Морган (1806–1871) – английский математик).
9. Закон двойного
дополнения
10. Законы поглощения
Докажем один из законной дистрибутивности:
Доказательство.
Чтобы доказать равенство двух множеств
А=В нужно доказать, что АВ
и ВА.
Докажем, что
Для доказательства этого включения
выберем произвольный элемент из множества
и покажем, что он принадлежит множеству
.
Итак, пусть
.
Тогда
и
.
Если
,
то
,
а значит,
.
Если
,
то
,
а значит,
.
Таким образом,
Теперь докажем,
что
Пусть
.
Если
,
то
и
,
отсюда следует, что
и
,
т.е.
.
Если
,
то
и
.
Отсюда следует, что
и
,
т.е.
.
Итак,
Таким образом, получили, что
и
,
а это значит, что эти два множества равны.
Доказательство можно оформить в более формализованном виде, используя “{” для системы высказываний, объединенных союзом “и”, “[”- для системы высказываний, объединенных союзом «или».
Докажем, один из
законов де Моргана:
.
С одной стороны,
.
С другой стороны,
Так как
и
,
то
,
что и требовалось доказать.
Утверждение 1.2.2. Следующие предложения о произвольных множествах попарно эквивалентны:
1)
;
2)
;
3)
;
4)
;
5)
.
Доказательство.
1
2. Так как
,
то достаточно показать, что
влечет
.
Но если
,
то по условию
,
и, следовательно,
.
2
3. Так как
,
то
.
По закону поглощения и закону
коммутативности имеем
.
Тогда
.
3
4. Предположим, что
.
Так как
,
то по закону де Моргана, закону
ассоциативности, закону коммутативности,
закону комплиментарности и закону 4
имеем
.
4
5. Предположим, что
,
т. е.
.
Тогда
.
По закону де Моргана и закону двойного
отрицания получаем
.
5
1. Предположим, что
и не выполняется условие
,
т. е. найдется элемент x
такой, что
и
.
Тогда
и, значит,
,
а это противоречит равенству
.
Отметим, что
операция \ выражается через операции
и
.
По закону де Моргана и закону двойного
отрицания справедливо соотношение
,
т. е. операция
также выражается через операции
и
.
По определению операция
тоже выражается через
и
.
Таким образом, любая из определенных
операций над множествами выражается
через операции
и
.
Пересечение и
объединение могут быть определены для
любого множества множеств
,
где индексы
пробегают множество
.
Пересечение
{
|
}
и объединение
{
|
}
задаются равенствами
{
|
}
= {
|
для всех
},
{
|
}
= {
|
для некоторого
}.
Вместо
{
|
}
и
{
|
}
часто пишут соответственно
и
,
а иногда просто
,
,
если из контекста ясно, какое множество
I имеется в виду. Если
I = {1,2,…,n},
то
и
,
а также
и
.
Совокупность
множеств
называется покрытием множества X,
если
Если при этом
>0
и
для всех i
,
то
называется разбиением множества
X.
Пример. Пусть X={a, b, c, d, e, f}. Тогда {{a, b, d }, {c, f}, {e}} – разбиение множества X, а {{a, b, d }, {в, c, f}, {в, e}} – покрытие множества X.
Одним из важных понятий теории множеств является понятие декартова произведения множеств. Декартовым (прямым) произведением множеств X и Y называется множество упорядоченных пар вида
{(x,y)
x
и
}.
Пример. Пусть
X={1,2}, Y={3,4,5}.
Тогда
{(1,3),
(1,4), (1,5), (2,3), (2,4), (2,5)},
{(3,1),
(3,2), (4,1), (4,2), (5,1), (5,2)},
{(1,1),
(1,2), (2,1), (2,2)}.
Две пары (x,y) и (u,v) считаются равными тогда и только тогда, когда x=u и y=v
Аналогично можно
определить декартово произведение n
множеств
Если
,
то n-я степень множества X
определяется как
Пример. Множество
|
Рис.
1.6 |
равно множеству
,
которому соответствует множество
точек на плоско-сти, имеющих
неотрицате-льные координаты, не
превос-ходящие единицы (рис. 1.6).