
- •Введение
- •1. Лекция №1
- •1.1. Предмет механики жидкости и газа
- •1.2. Краткие исторические сведения о развитии науки
- •1.3. Физическое строение жидкостей и газов
- •1.4. Основные физические свойства: сжимаемость, текучесть, вязкость, теплоемкость, теплопроводность
- •2. Лекция №2
- •2.1. Гипотеза сплошности
- •2.2. Два режима движения жидкостей и газов
- •2.3. Неньютоновские жидкости
- •2.4. Термические уравнения состояния
- •2.5. Растворимости газов в жидкостях, кипение, кавитация. Смеси
- •3. Лекция №3
- •3.1. Два метода описания движения жидкостей и газов
- •3.2. Понятие о линиях и трубках тока. Ускорение жидкой частицы
- •3.3. Расход элементарной струйки и расход через поверхность
- •3.4. Уравнение неразрывности (сплошности)
- •4. Лекция №4
- •4.1. Массовые и поверхностные силы
- •4.2. Поверхностные силы и напряжения
- •4.3. Напряжения поверхностных сил
- •4.4. Уравнения движения в напряжениях
- •5. Лекция №5
- •5.1. Уравнения гидростатики в форме Эйлера и их интегралы
- •5.2. Напряжения сил вязкости, обобщенная гипотеза Ньютона
- •5.3. Уравнение Навье-Стокса для вязкой жидкости
- •6. Лекция №6
- •6.1. Модель идеальной (невязкой) жидкости. Уравнения Эйлера
- •6.2. Интегралы уравнения движения жидкости для разных случаев движения. Баротропные и бароклинные течения
- •7. Лекция №7
- •7.1. Закон изменения количества движения
- •7.2. Закон изменения момента количества движения
- •7.3. Силовое воздействие потока на ограничивающие его стенки
- •8. Лекция №8
- •8.1. Уравнение баланса энергии
- •8.2. Турбулентное течение
- •9. Лекция №9
- •9.1. Подобие гидромеханических процессов
- •9.2. Понятие о методе размерностей. Пи-теорема
- •9.3. Роль чисел подобия
- •10. Лекция №10
- •10.1. Одномерные потоки жидкостей и газов
- •10.2. Уравнение д. Бернулли для струйки и потока реальной (вязкой) жидкости
- •10.3. Гидравлические потери (общие сведения)
- •11. Лекция №11
- •11.1. Ламинарное течение в круглых трубах
- •11.2. Течение при больших перепадах давления
- •12. Лекция №12
- •12.1. Потери напора при турбулентном течении в гидравлически гладких круглых трубах
- •12.2. Потери напора при турбулентном течении в шероховатых трубах. График и.И. Никурадзе
- •13. Лекция №13
- •13.1. Местные гидравлические сопротивления
- •13.2. Внезапное расширение русла
- •13.3. Внезапное сужение русла
- •13.4. Местные сопротивления при ламинарном течении
- •14. Лекция №14
- •14.1. Истечение жидкости через отверстие в тонкой стенке при постоянном напоре
- •14.2. Истечение через насадки при постоянном напоре
- •15. Лекция №15
- •15.1. Истечение через отверстия и насадки при переменном напоре
- •15.2. Неустановившееся движение жидкости в трубах
- •15.3. Гидравлический удар
- •16. Лекция №16
- •16.1. Расчет простых трубопроводов
- •16.2. Основные задачи по расчету простых трубопроводов
- •16.3. Последовательное соединение простых трубопроводов
- •16.4. Параллельное соединение простых трубопроводов
- •16.5. Разветвлённое соединение простых трубопроводов
- •17. Лекция №17
- •17.1. Расчет сложных трубопроводов
- •17.2. Трубопроводы с насосной подачей жидкости
- •17.3. Основы расчета газопроводов
- •Заключение
- •Библиографический список
- •Оглавление
- •Гоувпо «Воронежский государственный технический университет»
- •394026 Воронеж, Московский просп., 14
15.3. Гидравлический удар
Гидравлическим ударом обычно называют резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока жидкости. Гидроудар представляет собой колебательный процесс, возникающий в упругом трубопроводе с капельной жидкостью при внезапном изменении ее скорости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления. Изменение давления при этом тесно связано с упругими деформациями жидкости и стенок трубопровода. Гидроудар чаще всего возникает при быстром закрытии или открытии крана или иного устройства управления потоком. Однако могут быть и другие причины его возникновения.
Пусть в конце трубы, по которой жидкость
движется со скоростью
![]() ,
произведено мгновенное закрытие
крана (рис. 15.3, а).
,
произведено мгновенное закрытие
крана (рис. 15.3, а).

Рис. 15.3. Стадии гидравлического удара
Тогда скорость
частиц жидкости, натолкнувшихся на
кран, будет
погашена, а их кинетическая энергия
перейдет в работу деформации стенок
трубы и жидкости. При этом стенки трубы
растягиваются, а жидкость сжимается в
соответствии с повышением давления
![]() .
На заторможенные частицы у крана набегают
другие, соседние с ними частицы и тоже
теряют скорость, в результате чего
сечение n-n
перемещается вправо со скоростью с,
называемой скоростью ударной волны;
сама же переходная область, в которой
давление изменяется на величину
,
называется ударной волной. Когда ударная
волна переместится до резервуара,
жидкость окажется остановленной и
сжатой во всей трубе, а стенки трубы -
растянутыми. Ударное повышение давления
распространится на всю трубу (рис. 15.3,
б).
.
На заторможенные частицы у крана набегают
другие, соседние с ними частицы и тоже
теряют скорость, в результате чего
сечение n-n
перемещается вправо со скоростью с,
называемой скоростью ударной волны;
сама же переходная область, в которой
давление изменяется на величину
,
называется ударной волной. Когда ударная
волна переместится до резервуара,
жидкость окажется остановленной и
сжатой во всей трубе, а стенки трубы -
растянутыми. Ударное повышение давления
распространится на всю трубу (рис. 15.3,
б).
Но такое состояние не является равновесным.
Под действием перепада давления
частицы жидкости устремятся из трубы
в резервуар, причем это движение начнется
с сечения, непосредственно прилегающего
к резервуару. Теперь сечение n-n
перемещается в обратном направлении -
к крану - с той же скоростью с, оставляя
за собой выравненное давление
![]() (рис. 15.3, в). Жидкость
и стенки трубы предполагаются упругими,
поэтому они возвращаются к прежнему
состоянию, соответствующему давлению
.
Работа деформации полностью переходит
в кинетическую энергию, и жидкость в
трубе приобретает первоначальную
скорость
,
но направленную теперь в противоположную
сторону. С этой скоростью «жидкая
колонна» (рис. 15.3, г) стремится
оторваться от крана, в результате
возникает отрицательная
ударная волна под давлением
-
,
которая направляется от крана к резервуару
со скоростью с, оставляя за собой
сжавшиеся стенки трубы и расширившуюся
жидкость, что обусловлено снижением
давления (рис. 15.3, д). Кинетическая
энергия жидкости вновь переходит в
работу деформаций, но противоположного
знака. Состояние трубы в момент прихода
отрицательной ударной волны к резервуару
показано на рис. 15.3, е. Так же как и
для случая, изображенного на рис. 15.3,
б, оно не является равновесным. На
рис. 15.3, ж показан процесс выравнивания
давления в трубе и резервуаре,
сопровождающийся возникновением
движения жидкости со скоростью
.
Очевидно, что как только отраженная от
резервуара ударная волна под давлением
достигнет крана, возникнет ситуация,
уже имевшая место в момент закрытия
крана. Весь цикл гидравлического удара
повторится.
(рис. 15.3, в). Жидкость
и стенки трубы предполагаются упругими,
поэтому они возвращаются к прежнему
состоянию, соответствующему давлению
.
Работа деформации полностью переходит
в кинетическую энергию, и жидкость в
трубе приобретает первоначальную
скорость
,
но направленную теперь в противоположную
сторону. С этой скоростью «жидкая
колонна» (рис. 15.3, г) стремится
оторваться от крана, в результате
возникает отрицательная
ударная волна под давлением
-
,
которая направляется от крана к резервуару
со скоростью с, оставляя за собой
сжавшиеся стенки трубы и расширившуюся
жидкость, что обусловлено снижением
давления (рис. 15.3, д). Кинетическая
энергия жидкости вновь переходит в
работу деформаций, но противоположного
знака. Состояние трубы в момент прихода
отрицательной ударной волны к резервуару
показано на рис. 15.3, е. Так же как и
для случая, изображенного на рис. 15.3,
б, оно не является равновесным. На
рис. 15.3, ж показан процесс выравнивания
давления в трубе и резервуаре,
сопровождающийся возникновением
движения жидкости со скоростью
.
Очевидно, что как только отраженная от
резервуара ударная волна под давлением
достигнет крана, возникнет ситуация,
уже имевшая место в момент закрытия
крана. Весь цикл гидравлического удара
повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 15.4.
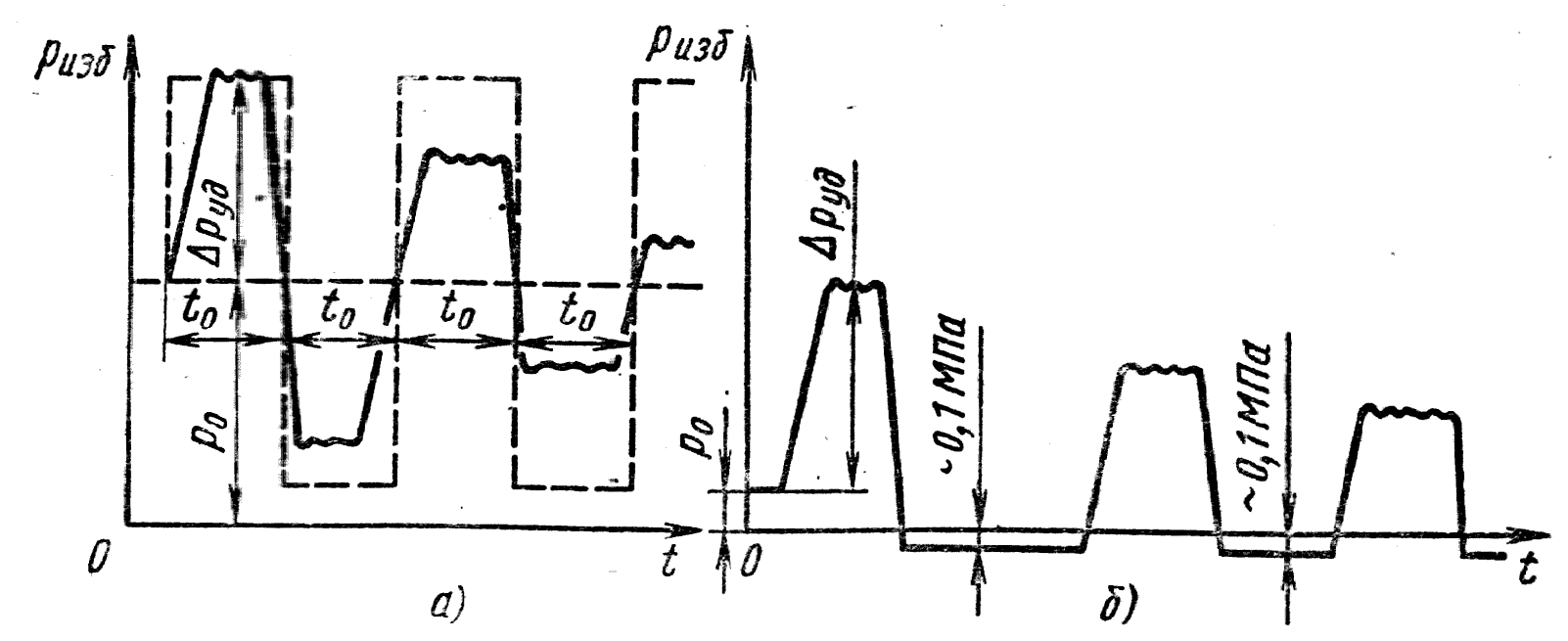
Рис. 15.4. Изменение давления в трубе
в процессе гидроудара
Диаграмма, показанная
штриховыми линиями на рис. 15.4, а,
характеризует теоретическое изменение
давления
![]() в точке А (рис.
15.3) непосредственно у крана (закрытие
крана предполагается мгновенным).
Сплошными линиями дан примерный вид
действительной картины изменения
давления по времени. В действительности
давление нарастает (а также падает),
хотя и круто, но не мгновенно. Кроме
того, имеет место затухание колебаний
давления, т.е. уменьшение его амплитудных
значений из-за трения и ухода энергии
в резервуар.
в точке А (рис.
15.3) непосредственно у крана (закрытие
крана предполагается мгновенным).
Сплошными линиями дан примерный вид
действительной картины изменения
давления по времени. В действительности
давление нарастает (а также падает),
хотя и круто, но не мгновенно. Кроме
того, имеет место затухание колебаний
давления, т.е. уменьшение его амплитудных
значений из-за трения и ухода энергии
в резервуар.
Повышение давления легко связать со скоростями и с, если рассмотреть элементарное перемещение ударной волны dx за время dt и применить к элементу трубы dx теорему об изменении количества движения. При этом получим
![]() .
(15.22)
.
(15.22)
Отсюда скорость распространения ударной волны
![]() ,
,
откуда
![]() .
(15.23)
.
(15.23)
Выражение (15.23) называют формулой Н.Е. Жуковского.
Но пока неизвестна скорость с, поэтому ударное давление найдем другим путем, а именно из условия, что кинетическая энергия жидкости переходит в работу деформации: растяжения стенок трубы и сжатия жидкости. Кинетическая энергия жидкости в трубе радиусом r равна
![]() .
(15.24)
.
(15.24)
Работа деформации равна потенциальной
энергии деформированного тела и
составляет половину произведения силы
на удлинение. Выражая работу деформации
стенок трубы как работу сил давления
на пути
![]() (рис.
15.5, а), получаем:
(рис.
15.5, а), получаем:
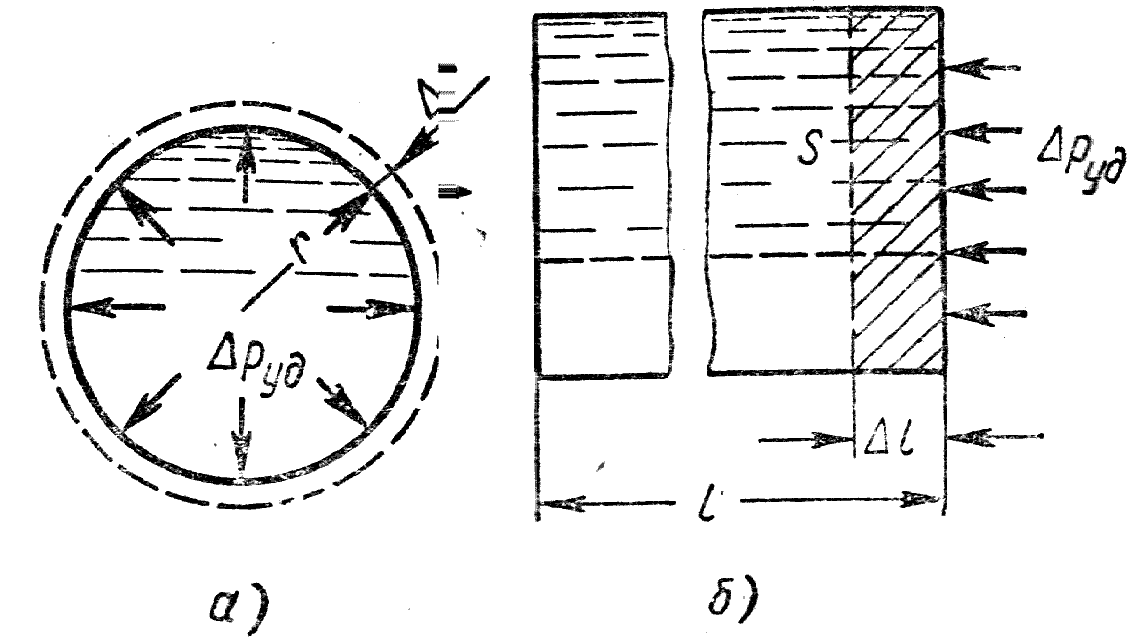



Рис. 15.5. Схема деформации трубы и жидкости
![]() .
(15.25)
.
(15.25)
По закону Гука
![]() ,
(15.26)
,
(15.26)
где
- нормальное напряжение в материале
стенки трубы, которое связано с давлением
и толщиной стенки
![]() соотношением
соотношением
![]() .
(15.27)
.
(15.27)
Выразив из уравнения (15.26), а из уравнения (15.27), получим работу деформации стенок трубы:
![]() .
(15.28)
.
(15.28)
Работу сжатия жидкости объемом V
можно представить как работу сил давления
на пути
![]() (рис. 15.5, б), т.е.
(рис. 15.5, б), т.е.
![]() .
(15.29)
.
(15.29)
Аналогично закону Гука для линейного
удлинения относительное уменьшение
объема жидкости
![]() связано с давлением зависимостью
связано с давлением зависимостью
![]() ,
(15.30)
,
(15.30)
где K - среднее для данного значение адиабатного модуля упругости жидкости.
Приняв за V объем жидкости в трубе, получим выражение работы сжатия жидкости в виде:
![]() .
(15.31)
.
(15.31)
Таким образом, уравнение энергий примет вид:
![]()
или
![]() .
(15.32)
.
(15.32)
Решая его относительно , получим формулу Н.Е. Жуковского в виде:
![]() .
(15.33)
.
(15.33)
Таким образом, скорость распространения ударной волны определяется выражением:
![]() .
(15.34)
.
(15.34)
