7.3. Силовое воздействие потока на ограничивающие его стенки

Для материального тела массой m, движущегося со скоростью , изменение количества движения за время dt вследствие действия силы выразится векторным уравнением

, (7.17)

где - приращение количества движения, обусловленное импульсом .

Применим эту теорему механики к участку потока с расходом Q между сечениями 1-1 и 2-2 в условиях установившегося течения (рис. 7.1).

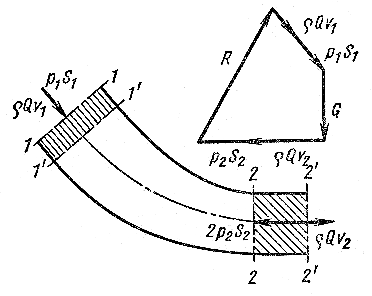
Рис. 7.1. Схема применения уравнения количества

движения к жидкости

За время dt этот участок переместится в положение, определяемое сечениями 1'-1' и 2'-2'. Чтобы выразить приращение количества движения рассматриваемого участка, нужно из количества движения объема между сечениями 1-1 и 2-2 вычесть количество движения объема между сечениями 1’-1’ и 2'-2'. При вычитании количество движения промежуточного объема, ограниченного сечениями 1'-1’ и 2-2, сократится и останется лишь разность количеств движения элементов 2-2' и 1-1', которые на рис. 7.1 заштрихованы. Объемы этих элементов , а следовательно, и их массы одинаковы, поэтому приращение количества движения будет равно .

Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объем жидкости между сечениями 1-1 и 2-2, - сил давления в первом и втором сечениях и , силы тяжести всего объема G, а также реакции стенок русла R, которая складывается из сил давления и трения, распределенных по боковой поверхности объема. Обозначим вектор равнодействующих всех сил через . Тогда

, (7.18)

или после сокращения на dt

. (7.19)

Таким образом, при установившемся движении вектор равнодействующей всех внешних сил, действующих на жидкость в фиксированном объеме, равен геометрической разности количеств движения жидкости, вытекающей из этого объема и втекающей в него за единицу времени.

Уравнение (7.19) можно записать в виде

(7.20)

и в соответствии с этим построить замкнутый треугольник (или многоугольник) векторов, как показано на рис. 7.1. В связи с тем что в уравнении (7.20) вектор , имеет знак «минус», при построении он направлен в сторону, обратную действительному его направлению. То же уравнение (7.20) можно записать и в проекциях на ту или иную ось.

В качестве примера определим силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 90° (рис. 7.2). Известны площадь сечения потока S, скорость истечения и плотность жидкости .

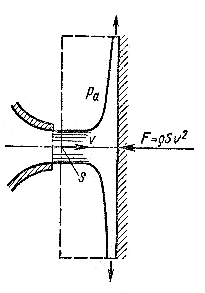
Рис. 7.2. Воздействие струи на преграду

Для решения данной задачи берем фиксированный объем, показанный штриховой линией. Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, для направления, совпадающего с вектором скорости истечения , уравнение будет

. (7.21)

Это и есть сила воздействия потока жидкости на преграду.