Глава 2. Нахождение минимальных и максимальных путей на орграфах
1. Нахождение кратчайших путей. Алгоритм Дейкстры
Пусть G={S,U,Ω} – ориентированный граф со взвешенными дугами. Обозначим s – вершину – начало пути и t – вершину конец пути. Веса дуг должны быть положительными.
Этап 1. Нахождение длины кратчайшего пути.
Шаг 1. Присвоение вершинам начальных меток.
Полагаем
и считаем эту метку постоянной (постоянные
метки помечаются сверху звёздочкой).
Для остальных вершин
полагаем
d(x)
= ∞ и считаем эти метки временными. Пусть
обозначение
текущей вершины.
Шаг 2. Изменение меток.
Для каждой вершины xi
с временной меткой, непосредственно
следует за вершиной
,
меняет её метку в соответствии со
следующим правилом:
(1)
Шаг 3. Превращение метки из временной в постоянную.
Из всех вершин с временными метками
выбираем вершину
с наименьшим значением метки:
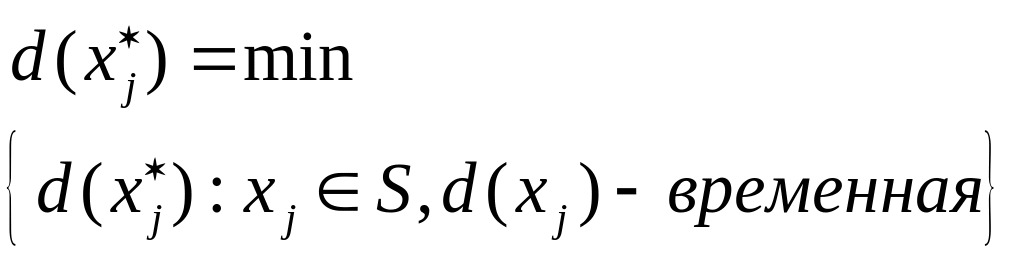(2)
Превращаем
эту метку в постоянную и полагаем
.
Шаг 4. Проверка на завершение первого этапа.
Если
-
длина кратчайшего пути от S
до t. В противном случае
происходит возвращение ко второму шагу.
Этап 2. Построение кратчайшего пути.
Шаг 5. Последовательный поиск дуг кратчайшего пути.
Среди вершин, непосредственно предшествующих вершине с постоянными метками, находим вершину хi, удовлетворяющую соотношению
.
(3)
Включаем дугу
в
искомый путь и полагаем
.
Шаг 6. Проверка на завершение второго этапа.
Если
,
то кратчайший путь найден – его образует
последовательность дуг, полученных на
пятом шаге и выстроенных в обратном
порядке. В противном случае возвращаемся
к пятому шагу.
Пример. Задана весовая матрица Ω сети G:
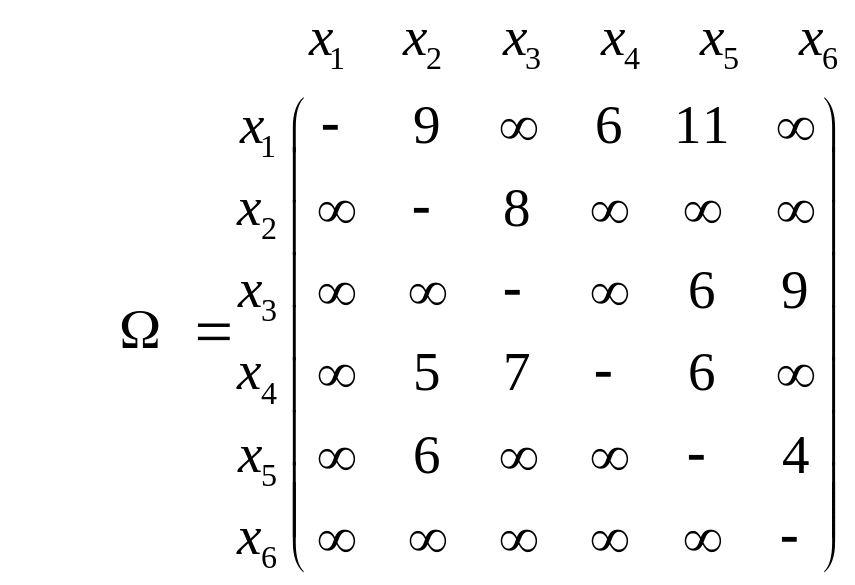
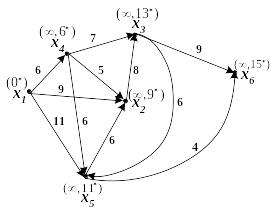
Рис. 34
Найти минимальный путь из вершины х1 в вершину х6 по алгоритму Дейкстры.
Решение. Т.к. в данном графе есть цикл между вершинами х2, х3 и х5, то вершины графа нельзя упорядочить по алгоритму Фалкерсона.
Этап 1.
Шаг 1.
Полагаем
.
Первая итерация.
Шаг 2.
Множество вершин, непосредственно
следующих за
с
временными метками
.
Пересчитываем временные метки этих
вершин.
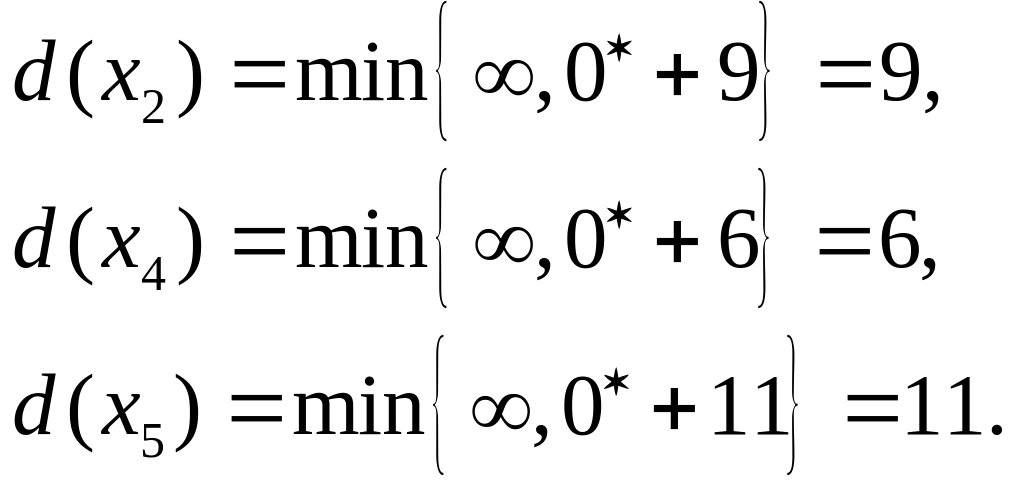
Шаг 3. Одна из временных меток превращается в постоянную:
Шаг 4.
происходит возвращение на второй шаг.
Вторая итерация.
Шаг 2.
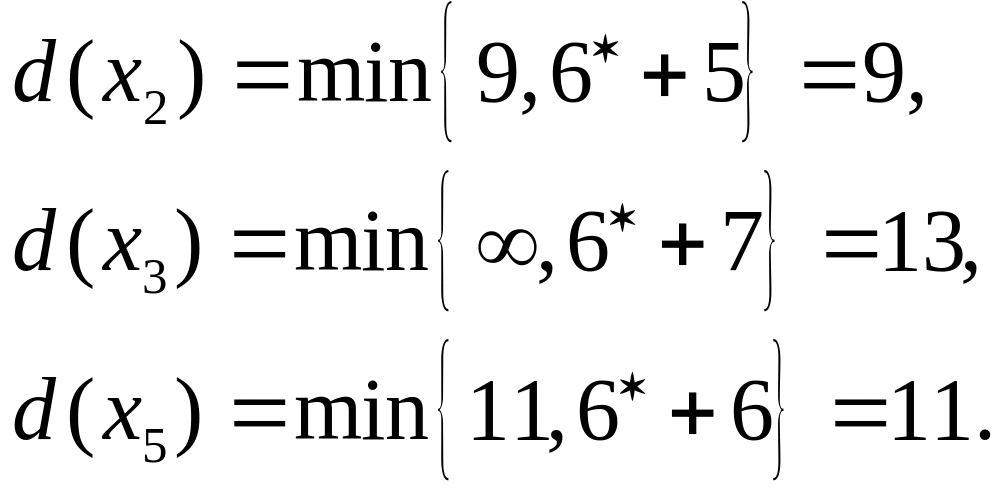
Шаг 3.
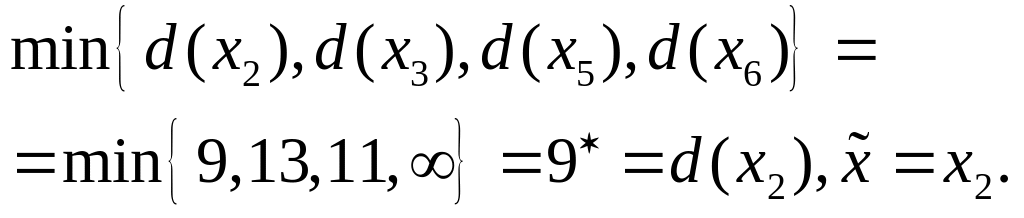
Шаг 4.
,
возвращение на 2-ой шаг.
Третья итерация.
Шаг 2.
Шаг 3.
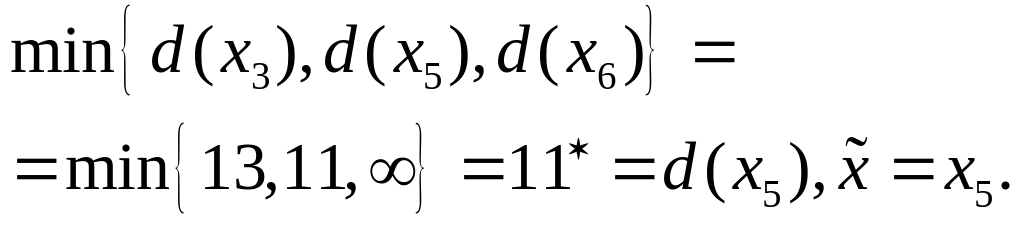
Шаг 4.
возвращение
на 2-ой шаг.
Четвёртая итерация.
Шаг 2.
Шаг 3.
Шаг 4.
возвращение
на 2-ой шаг.
Пятая итерация.
Шаг 2.
Шаг 3.
Шаг 4.
конец
1-го этапа.
Этап 2.
Первая итерация.
Шаг 5.
Составим множество вершин, непосредственно
предшествующих
с постоянными метками
Проверим для этих двух вершин выполнение равенства (3):
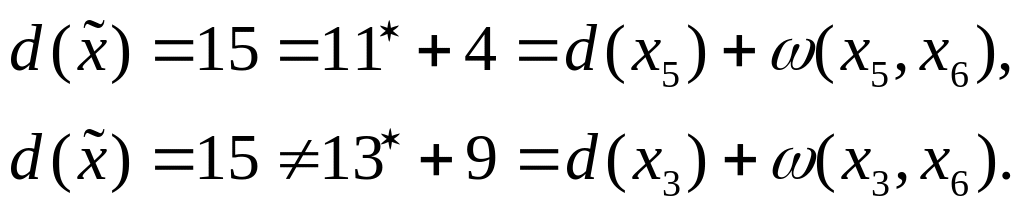
Включаем дугу
(х5,х6) в
кратчайший путь.
.
Шаг 6.
,
возвращение на 5-ый шаг.
Вторая итерация.
Шаг5.
Включаем дугу (х1,х5)
в кратчайший путь.
.
Шаг 6.
,
завершение второго этапа.
Итак
кратчайший путь от вершины х1
до вершины х6
построен. Его длина (вес) равен 15, сам
путь образует следующая последовательность
дуг:
