4.3.7. Программирование счетчиков

Рассмотренные схемы счетчиков считают количество импульсов в двоичной системе счисления. Такое изменение состояний выходов триггеров счетчика называют естественным и счетчик характеризуется модулем счета М (числом возможных состояний счетчика) равным 2ⁿ, где n – число разрядов счетчика. Емкость такого счетчика зависит от количества триггеров и равна М-1. Можно ввести понятие цикла работы счетчика (коэффициента пересчета), которое определяется минимальным количеством импульсов, поступление которых на счетный вход счетчика приводит его в исходное состояние. Эта величина совпадает с введенным ранее коэффициентом деления и модулем счета.

Чтобы получить иной модуль счета (коэффициент пересчета) и емкость счетчика, надо ввести обратные связи между триггерами таким образом, чтобы изменить естественный порядок смены состояний триггеров. Сделать это можно разными способами.

Можно сделать так, чтобы при состоянии триггеров, когда в счетчике записано число на единицу меньшее требуемого модуля счета (коэффициента пересчета), подготовить обратными связями такие уровни сигналов на входах триггеров, которые с поступлением следующего входного импульса переведут счетчик в исходное (нулевое для суммирующего счетчика) состояние.

Рассмотрим построение счетчика с емкостью десять (десятый импульс должен перевести его в исходное состояние). Для его построения необходимо четыре триггера (меньшее количество триггеров не сможет обеспечить требуемую емкость). Работа такого счетчика описана в таблице 4.13.

Из таблицы видно, что после состояния счетчика 1001 (на вход счетчика поступило девять импульсов) должно наступить состояние 0000, после чего счет начинается заново. Но следующий поступающий на его вход импульс при естественном изменении состояний триггеров должен перевести их выходы в состояние 1010. Таким образом, чтобы задать требуемый порядок изменения состояний триггеров, надо следующим входным импульсом первый и четвертый триггеры перевести в нулевое состояние.

Работа счетчика

Емкостью 10 Таблица 4.13

Номер импульса	Выходы Q4 Q3 Q2 Q1
исх. сост. 1 2 3 4 5 6 7 8 9 10	0 0 0 0 0 0 0 0 1 1 0	0 0 0 0 1 1 1 1 0 0 0	0 0 1 1 0 0 1 1 0 0 0	0 1 0 1 0 1 0 1 0 1 0

При этом необходимо запретить перевод второго триггера в единичное состояние при изменении сигнала на выходе первого триггера из 1 в 0, что должно бы реально произойти в двоичном счетчике. После девятого импульса его состояние не должно изменяться при поступлении очередного импульса. Он должен сохранить свое нулевое состояние. Такой алгоритм работы можно реализовать при введении обратных связей с выходов триггеров (рис.4.35). Такой счетчик называется декадным (десятичным).

Рис.4.35. Декадный счетчик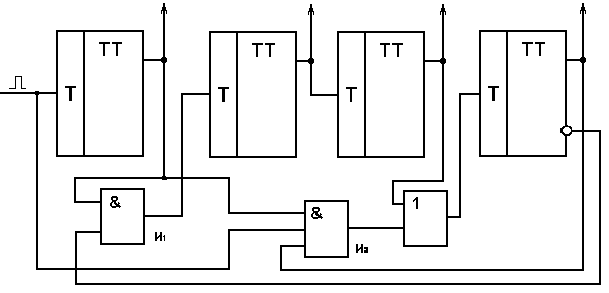

До восьмого импульса счетчик работает в естественном порядке смены состояний триггеров. Элемент И1 открыт единичным уровнем с инверсного выхода четвертого триггера.

Импульсы на вход четвертого триггера с выхода третьего проходят через элемент ИЛИ, через который может пройти и импульс с выхода элемента И2. Элемент И2 после девятого входного импульса подготовлен сигналом с прямых выходов первого и четвертого триггеров для того, чтобы пропустить на вход четвертого триггера импульс с входа счетчика, который переведет его в нулевое состояние. После восьмого импульса сигнал нулевого уровня с инверсного выхода четвертого триггера закроет элемент И1 для прохождения на вход второго триггера импульсов с выхода первого, т.к. второй триггер далее не должен переключаться. Первый триггер будет переключаться как и при естественном порядке смены его выходных уровней при поступлении входного импульса.

Таким образом, на входы второго и четвертого триггеров импульсы переключения проходят в зависимости от состояния четвертого триггера: если на его прямом выходе уровень нуля, то они проходят в естественном порядке через схемы И1, И2 и ИЛИ, если уровень логической единицы, то естественный порядок меняется, при поступлении десятого импульса первый и четвертый триггеры перейдут в нулевое состояние и на выходе счетчик будет 0.

Изменение естественного порядка счета импульсов можно сделать и иначе. Например, можно при поступлении максимального (в нашем случае, десятого) импульса перевести второй и четвертый триггеры в нулевое состояние. Сбрасывать второй триггер необходимо, так как при переходе первого триггера из 1 в 0, что произойдет при поступлении на его вход десятого входного импульса, и второй триггер может перейти в единичное состояние. Сигнал сброса формируется схемой совпадения (логическое И), на которую поступают входной импульс и сигналы с выходов первого и четвертого триггеров. С выхода схемы И сигнал сброса подают на установочные R-входы второго и четвертого триггеров (рис. 4.36). Тогда при поступлении десятого входного импульса, будет сброшен четвертый триггер, а второй триггер не изменит состояния 0.

Рис.4.36. Вариант декадного счетчика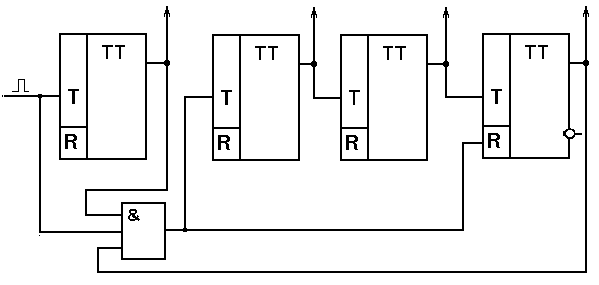

Для реализации декадного делителя частоты можно при поступлении девятого импульса перевести все триггеры в единичное состояние (наполнить счетчик) с тем, чтобы следующий (десятый) импульс записал в нем число 0000. Для этого достаточно после восьмого входного импульса подготовить канал для прохождения управляющего сигнала на установочные входы S, который переведет все триггеры в единичное состояние при поступлении девятого входного импульса (рис. 4.37).

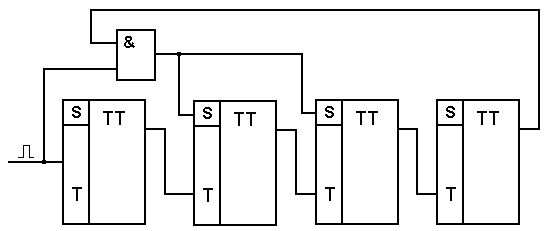
Рис.4.37. Декадный делитель частоты

Такой счетчик до восьмого импульса работает с естественным порядком изменения состояния. Девятый импульс переведет второй и третий триггеры в состояние 1 через элемент И, подготовленный к прохождению входного импульса единичным сигналом с прямого выхода четвертого триггера, при этом первый триггер переведется в единичное состояние входным импульсом, а четвертый останется в этом состоянии. В счетчике окажется записано число 1111. С поступлением десятого импульса все триггеры вернутся в исходное состояние – 0000.