
- •Кинематика. Динамика. Законы сохранения
- •210100.62 «Электроника и наноэлектроника»
- •223200.62 «Техническая физика» (профили «Физика и техника низких температур», «Физическая электроника»),
- •1. Кинематика
- •1.1. Основные формулы
- •1.2. Основные типы задач и методы их решения Классификация
- •Примеры
- •IV тип задач.
- •1.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •2. Динамика материальной точки и поступательного движения твердого тела
- •2.1. Основные формулы
- •2.2. Основные типы задач и методы их решения Классификация
- •Примеры решения задач
- •IV тип задач.
- •2.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •3. Работа, мощность, энергия. Законы сохранения
- •3.1. Основные формулы
- •3.2. Основные типы задач и методы их решения Классификация
- •Примеры
- •II тип задач
- •III тип задач
- •3.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •4. Динамика вращательного движения твердого тела
- •4.1. Основные формулы
- •4.2. Типы задач и методы их решения Классификация
- •Примеры
- •I тип задач
- •II тип задач
- •III тип задач
- •IV тип задач.
- •4.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •Библиографический список
- •Содержание
- •Кинематика. Динамика. Законы сохранения
- •210100.62 «Электроника и наноэлектроника»
- •223200.62 «Техническая физика» (профили «Физика и техника низких температур», «Физическая электроника»),
- •394026 Воронеж, Московский просп., 14
3. Работа, мощность, энергия. Законы сохранения
3.1. Основные формулы
1. Работа и мощность переменной силы
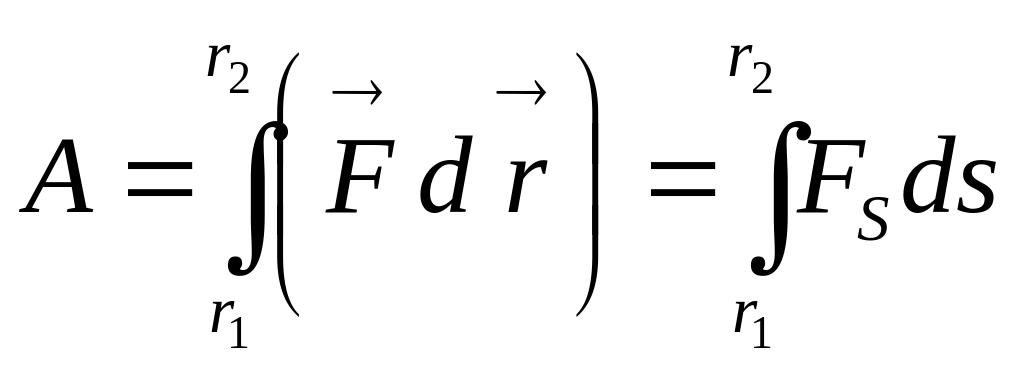 ,
,
![]() .
.
2. Приращение кинетической энергии частицы:
![]() ,
,
где А12 – работа всех сил, действующих на частицу.
3. Работа силы поля равна убыли потенциальной энергии частицы в данном поле:
![]() .
.
4. Связь между силой и потенциальной энергией частицы в поле:
![]() .
.
5. Приращение полной механической энергии системы:
![]() ,
,
где
![]() ,
U
– потенциальная энергия.
,
U
– потенциальная энергия.
Для замкнутой и консервативной систем
![]() .
.
6. Закон сохранения импульса для замкнутой системы
![]() .
.
3.2. Основные типы задач и методы их решения Классификация
1. Определение механической работы переменной силы.
Метод
решения.
Прямое интегрирование выражения
![]() или использование соотношения,
связывающего приращение механической
энергии с работой.
или использование соотношения,
связывающего приращение механической
энергии с работой.
2. Нахождение силы, действующей на частицу в потенциальном поле, и определение условий равновесия.
Метод
решения.
Использование соотношения
![]() ,
связывающего силу и потенциальную
энергию. Отыскание минимума и максимума
потенциальной энергии.
,
связывающего силу и потенциальную
энергию. Отыскание минимума и максимума
потенциальной энергии.
3. Столкновение частиц.
Метод решения. Применение законов сохранения импульса и энергии.
Примеры
I
тип задач.
Частица совершает перемещение в плоскости
из точки С(1,
2)м в точку D(2,
3)м. На частицу действует сила
![]() .
Определить работу силы.
.
Определить работу силы.
Решение
Элементарная
работа, совершаемая силой
,
при перемещении
![]()
![]() .
.
Тогда работа при перемещении частицы из точки С в точку D определится интегрированием
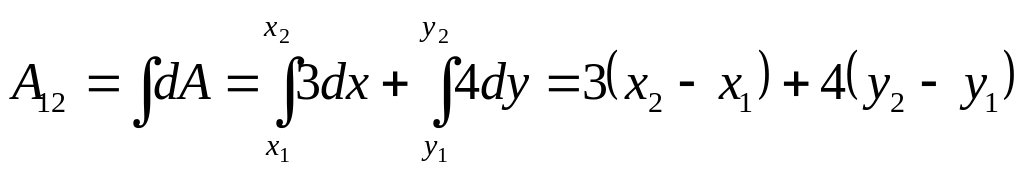 =
7 Дж.
=
7 Дж.
II тип задач
1.
Потенциальная энергия частицы имеет
вид
![]() ,
где а=const.
Найти: а) силу
,
действующую на частицу; б) работу А,
совершаемую над частицей силами поля
при переходе частицы из точки М(1,
1, 1) в точку N(2,
2, 3).
,
где а=const.
Найти: а) силу
,
действующую на частицу; б) работу А,
совершаемую над частицей силами поля
при переходе частицы из точки М(1,
1, 1) в точку N(2,
2, 3).
Решение
Используя
выражение, связывающее потенциальную
энергию частицы с силой, действующей
на нее, получим![]() Для
потенциального поля работа сил поля
равна убыли потенциальной энергии:
Для
потенциального поля работа сил поля
равна убыли потенциальной энергии:
![]() .
.
По
известным координатам точек 1 и 2 находим
U1
и U2.
Получаем значение
![]() .
.
2. Потенциальная энергия частицы, имеющей одну степень свободы (х) описывается уравнением
![]() .
.
Имеются ли у частицы положения равновесия?
Решение
Исследуем функцию Ux на максимум и минимум с помощью первой и второй производных. Первая производная
![]() .
.
Из
уравнения
![]() находим критические значения х:
находим критические значения х:
![]() ;
;
![]() .
.
Вторая
производная
![]() .
.
И
Рис.
3.1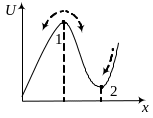
![]() (max);
(max);
![]() (min).
(min).
Таким образом, частица имеет два положения равновесия (рис. 3.1): неустойчивое ; устойчивое .
III тип задач
1
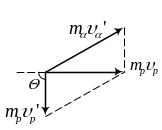 Рис.
3.2
Рис.
3.2![]() .
Считая массу
-частицы
в 4 раза больше массы протона, определить
энергию протона и
-частицы
после удара (
.
Считая массу
-частицы
в 4 раза больше массы протона, определить
энергию протона и
-частицы
после удара (![]() и
и
![]() ).
).
Решение
Введем
обозначения:
![]() -
скорость протона до удара;
-
скорость протона до удара;
![]() -
после удара;
-
после удара;
![]() -
скорость частицы после удара (до удара
она была равна нулю). По законам сохранения
импульса и энергии соответственно имеем
-
скорость частицы после удара (до удара
она была равна нулю). По законам сохранения
импульса и энергии соответственно имеем
![]() ;
(1)
;
(1)
![]() .
(2)
.
(2)
Для выполнения расчетов необходимо перейти от векторной формы записи уравнения (1) к скалярной. Это можно сделать, применив, как обычно, метод проекций. В данном случае можно поступить проще. Из треугольника импульсов (рис. 3.2) имеем:
![]() .
.
Решая это уравнение совместно с (2), находим
![]() =0,08МэВ;
=0,08МэВ;
![]() =0,12
МэВ.
=0,12
МэВ.
