Второй уровень сложности

1. Под каким углом α к горизонту нужно тянуть тяжелый ящик массы m для того, чтобы передвигать его волоком по горизонтальной поверхности с наименьшим усилием, если коэффициент трения равен μ? Найти значение этой минимальной силы. [F_min=mgsinα, α=arctgμ]

2. . Чему должен быть равен коэффициент трения между шинами и поверхностью наклонной дороги с уклоном =30⁰, чтобы автомобиль мог двигаться по ней вверх с ускорением a=0,6м/с²? [0,65]

Рис. 2.6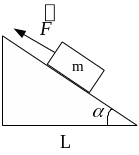

3. На наклонной плоскости (рис.2.6) лежит брусок массой m. К нему приложена сила , направленная вдоль наклонной плоскости в сторону ее вершины. Коэффициент трения между бруском и наклонной плоскостью . При каком угле наклона ускорение бруска будет минимальным и чему равно это ускорение? [ , а=8,5 м/с²]

4. За какое время тело соскользнет с наклонной плоскости высотой h=9,8 м и с углом наклона =60⁰ , если по наклонной плоскости с углом наклона =30⁰ оно движется вниз равномерно? [2 с]

5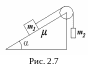 . Найти ускорение грузов в системе, если известны массы грузов m₁ и m₂ (m₂>m₁) и угол α, образуемый наклонной плоскостью с горизонтом (рис. 2.7). Рассмотреть задачу при наличии трения. [ ]

6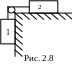 . Через невесомый блок, укрепленный на краю горизонтального стола, перекинута нерастяжимая легкая нить, связывающая грузы с массами =1кг и =2кг (рис. 2.8). Стол движется вверх с ускорением =1 м/с². Найти ускорение груза относительно стола ( ) и относительно земли (а). Трением пренебречь.

[ м/с²; м/с²]

7. При падении тела с большой высоты его максимальная скорость 80 м/с. Через какое время от начала падения скорость тела станет 20м/с? Силу сопротивления воздуха принять пропорциональной скорости движения тела. [2,3 с]

8. Диск радиусом R = 0,4 м вращается вокруг вертикальной оси. На краю диска лежит кубик. Принимая коэффициент трения =0,4, найти частоту п вращения, при которой кубик соскальзывает с диска. Решить задачу двумя способами: в неподвижной системе отсчета и в системе отсчета, связанной с диском. [п = 0,5 с^-1]

9. Горизонтальный диск вращается с постоянной угловой скоростью вокруг вертикальной оси, проходящей через его центр. По одному из диаметров диска движется тело массой m с постоянной относительно диска скоростью . Найти силу, с которой диск действует на это тело в момент, когда оно находится на расстоянии R от оси вращения.

[ ]

10. Небольшое тело падает без начальной скорости на Землю на экваторе, h =10 м. В какую сторону и на какое расстояние х отклонится тело от вертикали за время падения? Сопротивлением воздуха пренебречь. [ ]

11. Ракета массой m = 3 т, запущенная с поверхности Земли вертикально вверх, поднимается с ускорением . Скорость и струи газов, вырывающихся из сопла, равна 1,2 км/с. Найти расход горючего. [ ]

12. Найти ускорение и скорость тележки, движущейся под действием горизонтальной силы F, если на тележке лежит песок, который высыпается через отверстие в платформе тележки со скоростью кг/с. В начальный момент тележка имела скорость и массу m₀. [ ; ]