2. Динамика материальной точки и поступательного движения твердого тела

2.1. Основные формулы

1. Основное уравнение динамики материальной точки и поступательного движения твердого тела

или ,

где - равнодействующая всех сил, приложенных к телу; m – масса; - ускорение; - импульс.

2. Силы в механике:

• Сила упругости: ,

где k – коэффициент упругости; х – абсолютная деформация.

• Сила гравитационного взаимодействия:

,

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояния между ними.

• Сила сопротивления: ,

где k – коэффициент сопротивления среды, - скорость тела.

• Сила трения скольжения: ,

где - коэффициент трения скольжения; N – сила нормального давления.

3. Радиус-вектор центра масс системы материальных точек

,

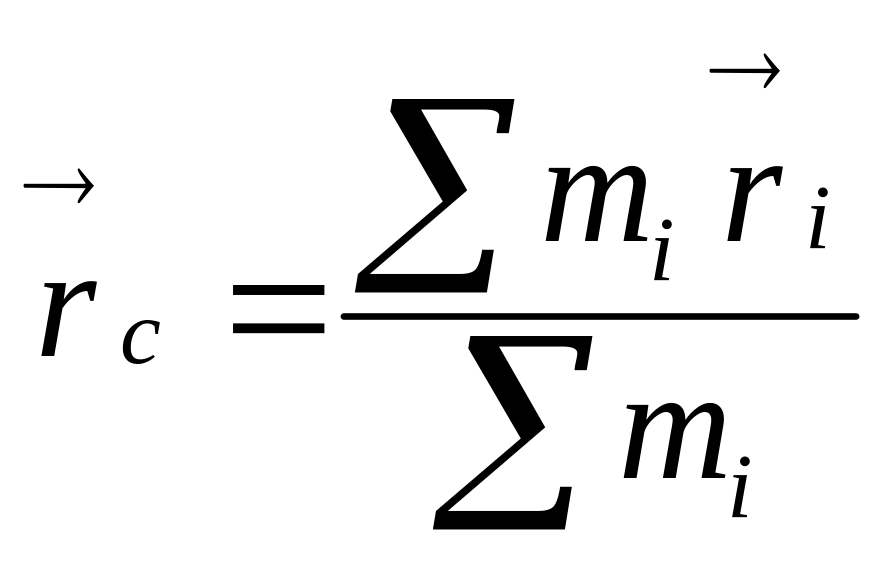где m_i , – масса и радиус-вектор i-й материальной точки.

4. Уравнение движения тела переменной массы (уравнение Мещерского)

,

где - скорость отделяемого (присоединяемого) вещества относительно рассматриваемого тела; - действующая сила; - реактивная сила.

5. II закон Ньютона в неинерциальной системе отсчета:

,

где - равнодействующая всех сил, приложенных к телу; - ускорение в неинерциальной системе отсчета; - сила инерции.

В неинерциальной системе отсчета, движущейся поступательно с ускорением : .

При движении тела относительно вращающейся системы отсчета сила инерции равна векторной сумме центробежной силы инерции и силы Кориолиса:

,

где - угловая скорость вращения системы отсчета; - радиус-вектор движущегося тела относительно оси вращения; - скорость его относительно подвижной системы.

2.2. Основные типы задач и методы их решения Классификация

1. Поступательное движение тел и простейших систем. Нахождение ускорений, сил.

Метод решения. Установить и представить на рисунке все силы, действующие на каждое тело системы. Написать уравнения движения для каждого из тел в отдельности в векторном виде. Перейти от векторов к их проекциям на соответствующим образом выбранное направление и решить систему получившихся скалярных уравнений.

2. Нахождение закона движения тел или , если известны действующие силы и начальные условия.

Метод решения. Анализ действующих на тело сил, составление уравнения движения в виде с последующим его интегрированием.

3. Движение тел переменной массы.

Метод решения. Использование уравнения Мещерского.

4. Движение тел в неинерциальных системах отчета.

Метод решения. Анализ всех реально действующих на тело сил и сил инерции. Использование второго закона Ньютона для неинерциальных систем отсчета.

Примеры решения задач

I тип задач. На горизонтальной плоскости лежит брусок с массой m₁, на который помещен груз с массой m₂ (рис. 2.1). Сила F приложена к грузу под углом к горизонту, коэффициент трения между плоскостью и бруском , между бруском и грузом . Найти ускорение обоих тел.

Решение

Р

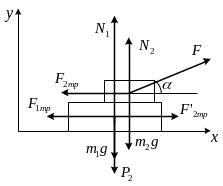Рис. 2.1

ассмотрим силы, действующие на каждое тело в отдельности. На груз действуют: сила , сила трения , сила тяжести груза и реакция опоры (бруска) . На брусок действуют сила трения (увлекает брусок вслед за грузом), сила тормозящего трения между бруском и плоскостью , сила тяжести бруска и вес груза , сила реакции опоры Согласно II закону динамики для груза и бруска имеем:

, (1)

. (2)

Выбрав оси координат, как показано на рис. 2.1 и проектируя векторные выражения (1) и (2) на оси х и у, получим:

Учитывая, что , , , находим ,

II тип задач. При падении тела с большой высоты его скорость при установившемся движении достигает значения м/с. Определить время , в течение которого, начиная от момента падения, скорость становится равной . Силу сопротивления воздуха принять пропорциональной скорости.

Решение

На падающее тело действуют сила тяжести и сила сопротивления воздуха , где k – коэффициент пропорциональности, зависящий от размеров, формы тела и свойств окружающей среды. Уравнение движения тела в векторной форме будет иметь вид:

. (1)

Спроектировав данное уравнение на вертикально направленную ось, имеем

. (2)

После разделения переменных получим

.

Интегрируя правую часть уравнения от нуля до , а правую соответственно от нуля до :

,

.

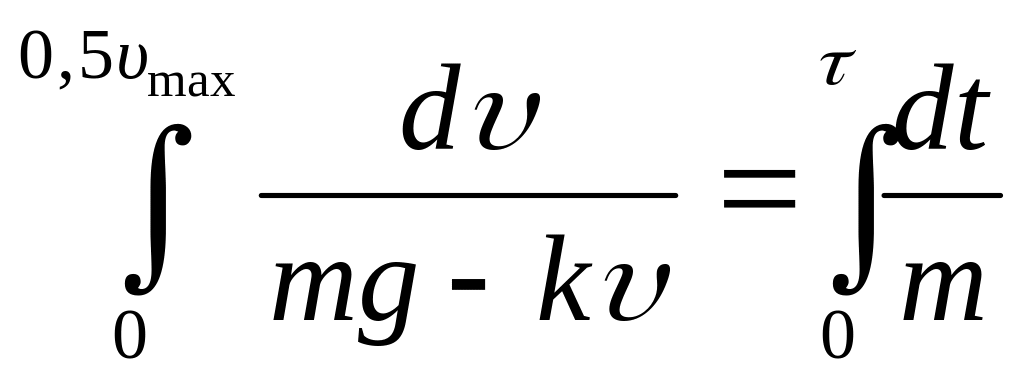После подстановки пределов интегрирования найдем

. (3)

Входящий в данные выражения коэффициент пропорциональности определим из условия равновесия сил для установившегося движения ( )

,

откуда .

Подставив найденное значение k в формулу (3), получим окончательно:

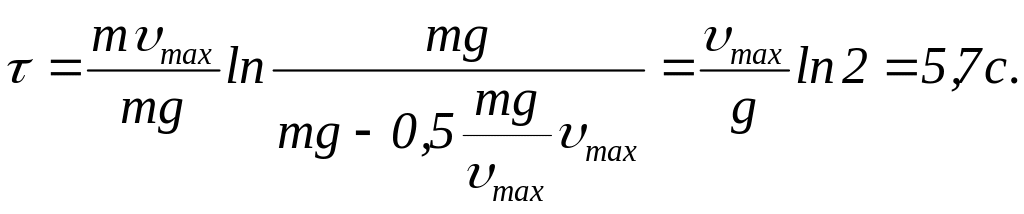
III тип задач. Ракета, масса которой в начальный момент кг, запущена вертикально вверх. Определить ускорение, с которым движется ракета через t = 5 с после запуска, если скорость расхода горючего кг/с, а относительная скорость выхода продуктов сгорания м/с. Сопротивление воздуха не учитывать.

Решение

Запишем уравнение Мещерского в проекции на вертикальную ось для момента времени t

. (1)

Масса ракеты изменяется со временем

. (2)

После подстановки и преобразования получаем

=32 м/с².