
- •Кинематика. Динамика. Законы сохранения
- •210100.62 «Электроника и наноэлектроника»
- •223200.62 «Техническая физика» (профили «Физика и техника низких температур», «Физическая электроника»),
- •1. Кинематика
- •1.1. Основные формулы
- •1.2. Основные типы задач и методы их решения Классификация
- •Примеры
- •IV тип задач.
- •1.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •2. Динамика материальной точки и поступательного движения твердого тела
- •2.1. Основные формулы
- •2.2. Основные типы задач и методы их решения Классификация
- •Примеры решения задач
- •IV тип задач.
- •2.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •3. Работа, мощность, энергия. Законы сохранения
- •3.1. Основные формулы
- •3.2. Основные типы задач и методы их решения Классификация
- •Примеры
- •II тип задач
- •III тип задач
- •3.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •4. Динамика вращательного движения твердого тела
- •4.1. Основные формулы
- •4.2. Типы задач и методы их решения Классификация
- •Примеры
- •I тип задач
- •II тип задач
- •III тип задач
- •IV тип задач.
- •4.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
- •Второй уровень сложности
- •Библиографический список
- •Содержание
- •Кинематика. Динамика. Законы сохранения
- •210100.62 «Электроника и наноэлектроника»
- •223200.62 «Техническая физика» (профили «Физика и техника низких температур», «Физическая электроника»),
- •394026 Воронеж, Московский просп., 14
IV тип задач.
1.
Маховик, вращающийся с постоянной
частотой п0=10об/с,
при торможении начал вращаться
равнозамедленно. Когда торможение
прекратилось, вращение снова сделалось
равномерным с частотой п
= 6 об/с. Определить угловое ускорение
![]() маховика и продолжительность t
торможения, если за время равнозамедленного
движения маховик сделал N
= 50 об.
маховика и продолжительность t
торможения, если за время равнозамедленного
движения маховик сделал N
= 50 об.
Решение
При равнопеременном вращательном движении законы изменения угловой скорости и углового пути описываются уравнениями
![]() ;
;
![]() .
(1)
.
(1)
Решение
этой системы уравнений дает соотношение,
связывающее угловое ускорение с начальной
![]() и конечной
и конечной
![]() угловыми скоростями:
угловыми скоростями:
![]() или
или
![]() .
(2)
.
(2)
Но
так как
![]() и
и
![]() ,
то
,
то
![]() .
.
Подставив
числовые значения в конечную формулу
для
![]() ,
получим:
,
получим:
![]() .
.
Угловое ускорение получилось отрицательным, так как маховик вращался замедленно.
Продолжительность
торможения определим из уравнения для
угловой скорости:
![]() ,
и с учетом выражения для
окончательно получим
,
и с учетом выражения для
окончательно получим
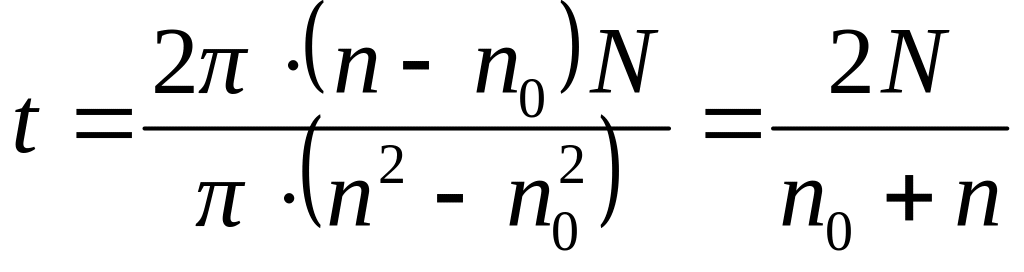 .
.
Время
торможения может быть найдено также по
формуле, связывающей угол поворота
![]() со средней угловой скоростью вращения
со средней угловой скоростью вращения
![]() и временем t:
и временем t:
![]() .
.
Откуда
![]() =
6,25 c.
=
6,25 c.
2. Твердое
тело вращается вокруг неподвижной оси
по закону
![]() ,
где а = 6,0 рад/с, в = 2,0 рад/с3.
Найти: 1) средние значения
угловой скорости и углового ускорения
за промежуток времени от t
= 0 до остановки; 2) угловое ускорение в
момент остановки тела.
,
где а = 6,0 рад/с, в = 2,0 рад/с3.
Найти: 1) средние значения
угловой скорости и углового ускорения
за промежуток времени от t
= 0 до остановки; 2) угловое ускорение в
момент остановки тела.
Решение
1) Используя закон изменения углового пути со временем, найдем последовательным дифференцированием законы изменения угловой скорости и углового ускорения:
![]() ,
,
![]() .
.
Время
остановки тела получим из первого
уравнения при
![]() :
:
![]() ,
откуда
,
откуда
![]() .
.
2)
Согласно определению
![]() ;
;
![]() .
.
Значения
углового пути
и угловой скорости
для
начального и конечного моментов времени
найдем путем подстановки
![]() и
и
![]() в соответствующие уравнения. Получим
в соответствующие уравнения. Получим
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Окончательно![]() ,
,
![]() рад/с2.
рад/с2.
3)
Угловое ускорение в момент остановки
тела получим из уравнения для углового
ускорения:
![]() рад/с2.
рад/с2.
1.3. Задачи для самостоятельного решения и контрольных заданий Первый уровень сложности
1.
Движение материальной точки описывается
уравнениями
![]() см,
см,
![]() см. Определить ускорение точки.[20
м/с2]
см. Определить ускорение точки.[20
м/с2]
2. За какую секунду свободного падения тело проходит путь 65 м? Начальная скорость тела равна нулю. [7]
3. Тело прошло половину пути со скоростью 6 м/с, а другую половину пути со скоростью 4 м/с. Чему равна средняя скорость тела на этом пути? [4,8 м/с]
4.
Велосипедист проехал первую половину
времени своего движения со скоростью
![]() =
16 км/ч, а
вторую половину со скоростью
=
16 км/ч, а
вторую половину со скоростью
![]() =
12 км/ч. Чему
равна средняя скорость движения
велосипедиста? [3,9 м/с]
=
12 км/ч. Чему
равна средняя скорость движения
велосипедиста? [3,9 м/с]
5. Тело брошено под углом 300 к горизонту со скоростью 20 м/с. Чему равен радиус кривизны траектории в точке броска и в верхней точке траектории. [47 м; 30 м]
6.
Частица движется со скоростью
![]() ,
А = 1 м/с. Каков модуль ускорения в момент
времени t
= 1 с? [5,4 м/с2]
,
А = 1 м/с. Каков модуль ускорения в момент
времени t
= 1 с? [5,4 м/с2]
7.
Движение частицы определяется уравнениями
x=4t,
y=2t2.
Чему равен
угол между
вектором скорости
![]() и вектором
ускорения
и вектором
ускорения
![]() в
момент времени t
= 1 с? [450]
в
момент времени t
= 1 с? [450]
8. Колесо радиусом R = 1 м вращается так, что зависимость угла поворота от времени дается уравнением φ =3 + 2t + t3 (рад). Чему равно через 2 с после начала движения тангенциальное ускорение точек, лежащих на ободе колеса? [12 м/с2]
9. Зависимость угла поворота колеса радиусом R = 0,1 м от времени дается уравнением φ = 3 + 2t +t3 (рад). Чему равно через одну секунду после начала движения нормальное ускорение точек, лежащих на ободе колеса? [2.5 м/с2]
10. Движение тела с неподвижной осью задано уравнением φ = 2π(6t – 3t2). Начало движения при t = 0. Сколько оборотов сделает тело до момента изменения направления вращения? [3]
11. Твердое тело вращается вокруг неподвижной оси по закону φ = 6t – 2t3. Чему равен модуль углового ускорения в момент остановки тела? [12 рад/с2]
12. Твердое тело вращается вокруг неподвижной оси по закону φ = 6t – 2t3. Каково среднее значение угловой скорости за промежуток времени от t = 0 до остановки? [4 рад/c]
13. Зависимость угла поворота колеса от времени дается уравнением φ = 5 + 5t + t3. Нормальное ускорение точек, лежащих на ободе колеса, к концу второй секунды движения составило 81 м/с2. Определить радиус колеса. [1 м]
