
- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1. Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •Линейное пространство.
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •1. Постановка задачи линейного программирования (злп)
- •2. Графический метод решения злп
- •3. Симплекс – метод решения злп
- •4. Двойственные злп
- •Методы определения опорного плана тз.
- •Вопросы для повторения.
- •Глава 6. Балансовые модели
- •1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 52
- •Глава 4. Векторная алгебра 103
- •Глава 5. Задачи линейного программирования 118
- •Глава 6. Балансовые модели 153
- •394026 Воронеж, Московский просп., 14
1.2. Числовые множества и их свойства.
Построение множества действительных чисел.

Рис. 2.
Структура множества действительных чисел представлена на рисунке 2.
Заметим, что для написания действительных чисел мы используем цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), которые придумали монахи-брамины в Индии; арабы же принесли их в Европу между X и XV столетиями.
Действительные числа образуют множество R элементов, обладающее следующими свойствами:
Упорядоченность. Для любых двух действительных чисел a и b определено отношение порядка, т.е. имеет место одно из отношений: a<b, a=b, a>b. При этом, если a<b и b<c, то a<c (транзитивность упорядоченности). Соотношения порядка называют также сравнением действительных чисел по величине.
Операция сложения. Для любой пары чисел
 определено такое единственное число,
называемое их суммой
a+b, что
выполняются условия:
II1.
a+b=b+a
(коммутативность);
II2.
a+(b+c)=(a+b)+c,
определено такое единственное число,
называемое их суммой
a+b, что
выполняются условия:
II1.
a+b=b+a
(коммутативность);
II2.
a+(b+c)=(a+b)+c,
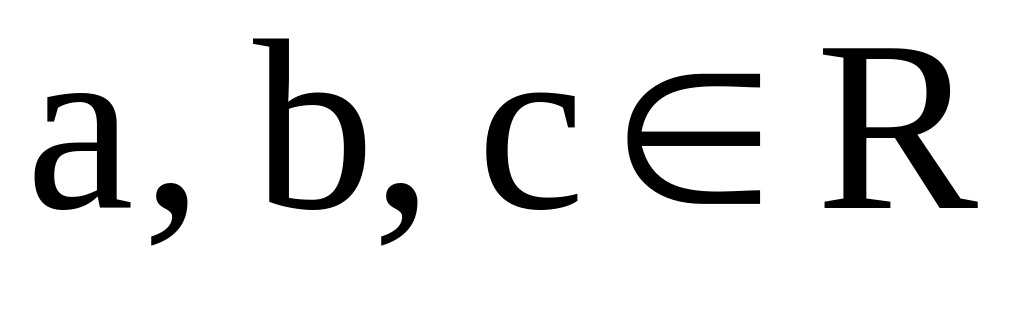 (ассоциативность);
II3.
существует единственное число, называемое
нулём
0,
такое, что a+0=a
для любого
(ассоциативность);
II3.
существует единственное число, называемое
нулём
0,
такое, что a+0=a
для любого
 ;
II4.
для любого числа
существует единственное число (-a),
называемое ему противоположным,
такое, что a+(-a)=0;
число a+(-b)=a-b,
,
называется разностью
чисел a и b;
II5.
если a<b,
то a+с<b+с
для любого
;
II4.
для любого числа
существует единственное число (-a),
называемое ему противоположным,
такое, что a+(-a)=0;
число a+(-b)=a-b,
,
называется разностью
чисел a и b;
II5.
если a<b,
то a+с<b+с
для любого
 .
.Операция умножения. Для любой пары вещественных чисел a и b определено такое единственное число, называемое их произведением ab, что выполняются условия: III1. ab=ba (коммутативность); III2. a(bc)=(ab)c, (ассоциативность); III3. существует единственное число 1, называемое единицей, такое, что a1=a для любого ; III4. для любого числа
 существует единственное число
существует единственное число
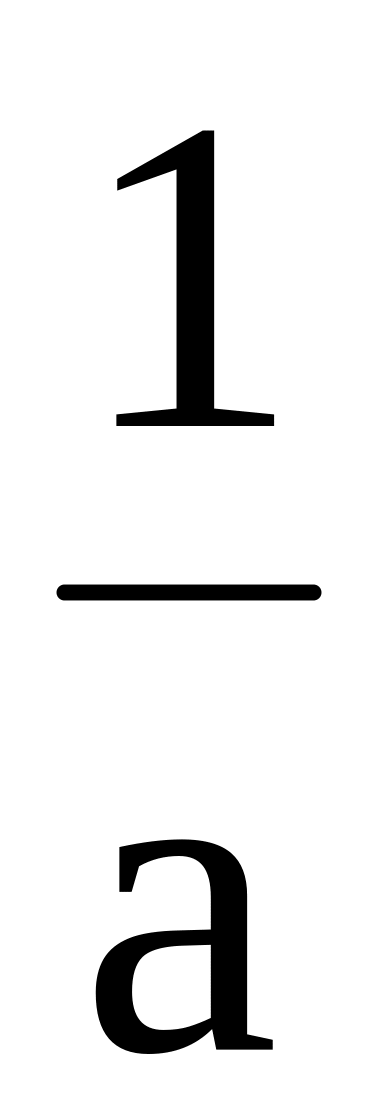 ,
называемое ему обратным
к данному, такое, что a
=1;
число a
,
называемое ему обратным
к данному, такое, что a
=1;
число a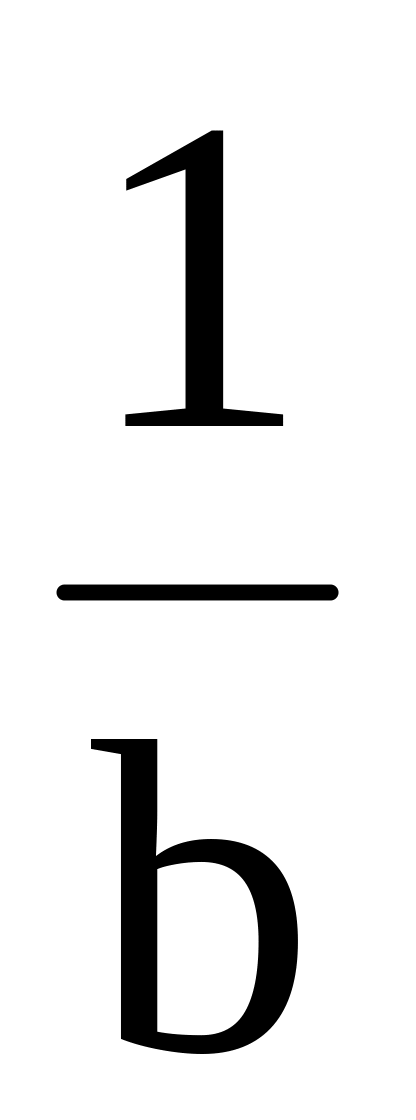 ,
,
 ,называется
частным
,называется
частным
 от
деления a на b;
III5.
если либо a,
либо b,
либо a и b равны 0, то ab=0; III6.
если a<b
и c>0,
то aс<bс,
если a<b
и c<0,
то aс>bс,
.
от
деления a на b;
III5.
если либо a,
либо b,
либо a и b равны 0, то ab=0; III6.
если a<b
и c>0,
то aс<bс,
если a<b
и c<0,
то aс>bс,
.Дистрибутивность умножения относительно сложения: (a+b)c=ac+bc для любых .
Плотность: для любых , таких, что a<b, существует такое число c, что a<c<b.
Непрерывность: для любых непустых числовых множеств X и Y, таких, что для каждой пары чисел
 и
и
 ,
,
выполняется
неравенство
![]() ,
существует число a, удовлетворяющее
условию:
,
существует число a, удовлетворяющее
условию:
![]() ,
,
.
,
,
.
Подмножества множества R.
Число 1+1 обозначают 2, число 2+1 обозначают 3 и т.д. Эти числа 1, 2, 3,
 ,
образуют множество
N натуральных чисел.
,
образуют множество
N натуральных чисел.Числа, большие 0, называются положительными числами, числа, меньшие 0 – отрицательными. Числа
 образуют множество
Z целых чисел.
образуют множество
Z целых чисел.Числа, представимые в виде несократимого отношения
 ,
,
 ,
,
 ,
образуют множество
Q рациональных чисел.
,
образуют множество
Q рациональных чисел.Действительные числа, не являющиеся рациональными, образуют множество I иррациональных чисел.
Множество R является объединением множеств Q и I:
 .
.
Свойство Архимеда. Каково бы ни было число , существует такое число , что n>a.
Следствие. Каковы бы ни были числа a и b, 0<a<b, существует такое число , что na >b.
Числовые промежутки.
Пусть
P(x) – какое-то свойство числа x. Тогда
запись
![]() означает множество
чисел, обладающих свойством P(x).
означает множество
чисел, обладающих свойством P(x).
Пусть даны два числа a и b, a<b. Рассмотрим следующие множества на числовой оси:
![]() -
отрезок
(сегмент)
[a,b];
-
отрезок
(сегмент)
[a,b];
![]() ,
,![]() -
полуинтервалы;
-
полуинтервалы;
![]() -
интервал
(a,b);
-
интервал
(a,b);
![]() или
или
![]() - полуоси
- полуоси
![]() или
или
![]() .
.
Все указанные множества называются промежутками.
Кванторы (логические символы).
![]() (для
любого, для каждого) – квантор
всеобщности.
(для
любого, для каждого) – квантор
всеобщности.
![]() (существует)
– квантор
существования.
(существует)
– квантор
существования.
Ограниченность множеств.
Числовое
множество X называется ограниченным
сверху (снизу),
если
![]() (если существует число c такое, что для
любого x из X выполняется неравенство
(если существует число c такое, что для
любого x из X выполняется неравенство
![]() ).
).
Множество, ограниченное сверху и снизу, называется ограниченным множеством.
Примеры: [2,3] – ограниченное множество;
![]() -
множество, ограниченное снизу;
-
множество, ограниченное снизу;
![]() -
множество, ограниченное сверху.
-
множество, ограниченное сверху.
Комплексные числа.
Комплексным
числом
называется выражение вида z=x+iy,
![]() ,
,
![]() -
мнимая
единица, то
есть число, квадрат которого равен -1.
-
мнимая
единица, то
есть число, квадрат которого равен -1.
x=Re z – действительная часть z.
y=Im z – мнимая часть z.
Действительное число x является частным случаем комплексного числа z=x+iy при y=0.
Если
x=0,
а
![]() ,
то числа вида z=iy называются мнимыми
числами.
,
то числа вида z=iy называются мнимыми
числами.
Комплексное число z=x+iy равно 0, если x=0 и y=0.
Два комплексных числа z1=x1+iy1 и z2=x2+iy2 называются равными, если x1= x2 и y1= y2.
Определение. Будем говорить, что между множествами X и Y установлено соответствие, если по какому-либо закону или правилу каждому элементу соответствует элемент . Соответствие называется взаимно-однозначным, если любому соответствует только один элемент и, наоборот, любому соответствует только один элемент .
Комплексные числа изображаются точками на комплексной плоскост (см. рис.3.).Плоскость называется комплексной, если каждому комплексному числу z=x+iy ставится в соответствие точка плоскости Z(x,y), причём это соответствие взаимно-однозначное.
Оси Ox и Oy прямоугольной (декартовой) системы координат, на которых расположены действительные числа z=x+0i=x и мнимые числа z=0+iy=iy, называются соответственно действительной и мнимой осями.

Рис.3. Комплексная плоскость
(x,0) – действительное число x;
(0,y) – мнимое число z=iy;
(0,1) – мнимая единица i;
(1,0) – действительное число 1;
(0,0) – z=0;
(x,y) – комплексное число z=x+iy.
Все эти числа изображены на рис.3.
С
каждой точкой M(x,y) комплексной плоскости
связан радиус-вектор этой точки
![]() ,
длина которого
,
длина которого
![]() называется
модулем
комплексного числа z.
называется
модулем
комплексного числа z.
Угол φ, образованный радиус-вектором с положительным направлением оси абсцисс, называется аргументом комплексного числа z.
![]()
(определён
неоднозначно с точностью до
![]() ).
).
Если
![]() ,
то
,
то
![]() ,
но угол φ не определён. Если дополнительно
сделать ограничение
,
но угол φ не определён. Если дополнительно
сделать ограничение
![]() ,
то угол φ определяется однозначно и
обозначается символом arg z.
,
то угол φ определяется однозначно и
обозначается символом arg z.
Число
![]() называется комплексно-сопряжённым
комплексному числу
называется комплексно-сопряжённым
комплексному числу
![]() .
Заметим, что произведение
.
Заметим, что произведение
![]() (действительное
число) (см. задачу ниже).
(действительное
число) (см. задачу ниже).
Множество всех комплексных чисел обозначается C.
Связь между числовыми множествами:
![]() .
.
Арифметические операции над комплексными числами.
Пусть даны комплексные числа z1=x1+iy1 и z2=x2+iy2. Тогда их сумма (разность) определяется как
![]()
Произведение определяется следующим образом:
![]()
Действительно,
![]() .
.
Так
как
![]() ,
получаем искомую формулу.
,
получаем искомую формулу.
Частное
двух комплексных чисел
![]() и
и
![]() получим,
домножая числитель и знаменатель на
число, сопряжённое знаменателю:
получим,
домножая числитель и знаменатель на
число, сопряжённое знаменателю:

По формуле умножения комплексных чисел имеем,
![]()
Задача. Доказать, что сумма и произведение комплексно-сопряжённых чисел есть число действительное.
Формы представления комплексных чисел.
Алгебраическая z=x+iy.
Тригонометрическая
 Из
алгебраической формы можно перейти в
тригонометрическую, действуя следующим
образом:
Из
алгебраической формы можно перейти в
тригонометрическую, действуя следующим
образом:
 где
где
 ,
.
В
тригонометрической форме очень удобно
умножать и делить комплексные числа.
Если z1=ρ1(cos
φ1+isin
φ1),
z2=ρ2(cos
φ2+isin
φ2),
то
,
.
В
тригонометрической форме очень удобно
умножать и делить комплексные числа.
Если z1=ρ1(cos
φ1+isin
φ1),
z2=ρ2(cos
φ2+isin
φ2),
то
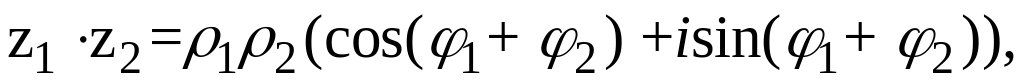
 .
.Показательная (экспоненциальная)
 .
.
Связь между экспоненциальной функцией и тригонометрическими функциями выражается с помощью формул Эйлера:
![]()
Возведение комплексного числа в натуральную степень n.
![]() (формула
Муавра).
(формула
Муавра).
Извлечение корня n-ой степени из комплексного числа.
![]() .
.
Корень
n-ой
степени из не равного нулю комплексного
числа имеет n различных значений, которые
геометрически являются вершинами
правильного n-угольника, вписанного в
окружность с центром в нуле и радиусом
![]() .
.
Пример.
Найти
![]() .
.
Решение.
Заметим, что
![]() ,
то есть
,
то есть
![]() ,
a
,
a
![]() .
.
Модуль
комплексного числа –i равен
![]() ;
;
Вычислим аргумент:
![]() .
.
Запишем число –i в тригонометрической форме:
![]() z.
z.
По формуле извлечения корня из комплексного числа, имеем:
=
Первый
корень получаем при![]() z1=
z1=![]() =0+i1=i;
=0+i1=i;
При
![]() :
:


Наконец,
третий корень найдём при k=2
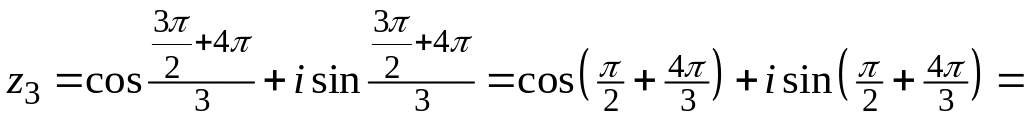
![]()

![]()
Результат
изображён на рис.4.
![]()
Рис.4. Значения
