9. Квадратичные формы

Числовая функция вида

Q(x₁, x₂, , x_n) = , (1)

где коэффициенты a_ij – действительные числа, такие, что a_ij = a_ji, называется квадратичной формой.

Квадратная матрица A n-го порядка, составленная из коэффициентов a_ij, , называется матрицей квадратичной формы. Она является симметрической матрицей, т.е. A = A^T. Ранг этой матрицы называется рангом квадратичной формы. Если rang A = n, т.е. матрица A –невырожденная, то и квадратичная форма Q называется невырожденной.

Распишем выражение (1).

Таким образом,

Q(x₁, x₂, , x_n) = (2)

Обычно выражение (2) записывают в виде Q(x₁, x₂, , x_n) = где b_ii = a_ii, , b_ij = 2a_ij, , .

Т.к. a_ij = a_ji, то матрица квадратичной формы Q будет иметь вид:

Матричное представление квадратичной формы.

Пусть X – вектор – столбец переменных x_j, .

Тогда X^T = - вектор – строка.

Составим произведение AX:

Умножим это равенство слева на X^T, то есть вычислим X^TAX: =

= Q(x₁, x₂, , x_n).

Q = X^TAX (3)

матричное представление квадратичной формы.

Линейное преобразование квадратичной формы.

Рассмотрим квадратичную форму (1). Перейдём к новым переменным y_i, , по формулам:

. (4)

или в матричном виде

X = BY, (5)

где

X = , Y = , B = . (6)

В квадратичной форме (1) вместо x_i подставим их выражения через y_i, , определяемые формулами (4).

Получим квадратичную форму F(y₁, y₂, , y_n) n переменных y₁, y₂, , y_n с некоторой матрицей C.

В этом случае говорят, что квадратичная форма Q(x₁, x₂, , x_n) переводится в квадратичную форму F(y₁, y₂, , y_n) линейным преобразованием (4).

Линейное преобразование называется невырожденным, если det B  0.

2 квадратичные формы называются эквивалентными Q(x₁, x₂, , x_n) ~ F(y₁, y₂, , y_n), если существует невырожденное линейное преобразование, переводящее одну из них в другую.

Cвойства эквивалентных квадратичных форм.

1. Рефлексивность. Q(x₁, x₂, , x_n) ~ Q(x₁, x₂, , x_n).

2. Симметричность. Если Q(x₁, x₂, , x_n) ~ F(y₁, y₂, , y_n), то F(y₁, y₂, , y_n) ~ Q(x₁, x₂, , x_n).

3. Транзитивность. Если Q(x₁, x₂, , x_n) ~ F(y₁, y₂, , y_n), F(y₁, y₂, , y_n) ~ (z₁, z₂, , z_n), то Q(x₁, x₂, , x_n) ~ (z₁, z₂, , z_n).

Теорема. Квадратичная форма (1) с матрицей A переводится линейным невырожденным преобразованием X = BY в квадратичную форму F(y₁, y₂, , y_n) с матрицей C = B^TAB.

Доказательство. Рассмотрим квадратичную форму Q = X^TAX. Подвергнем её линейному невырожденному преобразованию X = BY:

Q = (BY)^TA(BY) = Y^TB^TABY = Y^T(B^TAB)Y = Y^TCY = =F(y₁, y₂, , y_n), где C = B^TAB.

Следствие 1. Определители матриц эквивалентных невырожденных квадратичных форм имеют одинаковые знаки.

Следствие 2. Эквивалентные квадратичные формы имеют одинаковые ранги.

Классификация квадратичных форм.

Квадратичная форма (1) называется положительно (отрицательно) определённой, если Q(x₁, x₂, , x_n) > 0 (< 0) x_i, , : .

Квадратичная форма (1) называется положительно (отрицательно) полуопределённой, если Q(x₁, x₂, , x_n)  0 ( 0) x_i, .

Квадратичная форма (1) называется неопределённой, если 2 вектора и имеют квадратичные формы разных знаков: Q(x₁, x₂, , x_n) > 0 (< 0), Q(y₁, y₂, , y_n) < 0 (> 0).

Квадратичная форма (1) имеет канонический вид, если a_ij = 0 при i  j, , т.е. Q(x₁, x₂, , x_n) = . Матрица A квадратичной формы в этом случае имеет диагональный вид:

.

Теорема. Всякая квадратичная форма с помощью линейного невырожденного преобразования может быть приведена к каноническому виду.

Если в каноническом виде a_ii = 1  , то квадратичная форма (1) имеет нормальный вид.

Теорема. Всякую квадратичную форму можно привести линейным невырожденным преобразованием к нормальному виду: (z₁, z₂, , z_n) = , причём общее число входящих сюда квадратов равно рангу формы.

Закон инерции квадратичных форм.

Число положительных и отрицательных квадратов в нормальном виде, к которому приводится данная квадратичная форма линейным преобразованием не зависит от выбора этого преобразования.

Определение. Число i₊ (i_-) положительных (отрицательных) квадратов в той нормальной форме, к которой приводится данная квадратичная форма Q, называется положительным (отрицательным) индексом инерции этой формы.

Разность S между положительным и отрицательным индексами инерции S = i₊ - i_- называется сигнатурой формы Q.

Признак эквивалентности квадратичных форм.

Две квадратичные формы эквивалентны между собой тогда и только тогда, когда равны их ранги и сигнатуры.

Спектральный признак знакоопределённости квадратичной формы.

Для того, чтобы квадратичная форма (1) была положительно (отрицательно) определённой, необходимо и достаточно, чтобы спектр матрицы A квадратичной формы состоял только из положительных (отрицательных) чисел.

Определение. Миноры матрицы A квадратичной формы (1), расположенные в левом верхнем углу матрицы A

называются главными (угловыми) минорами матрицы A квадратичной формы (1).

Критерий Сильвестра. Для того, чтобы квадратичная форма (1) была положительно (отрицательно) определённой, необходимо и достаточно, чтобы (чтобы знаки угловых миноров чередовались, причём ).

Ортогональные матрицы.

Определение 1. Система векторов – столбцов квадратной матрицы A порядка n называется ортонормированной, если длина каждого вектора , и векторы – столбцы ортогональны, т.е. все скалярные произведения этих векторов равны нулю.

или в координатной форме: .

Определение 2. Квадратная матрица A называется ортогональной, если её столбцы представляют собой ортонормированную систему векторов.

Свойства ортогональной матрицы.

1. Для того, чтобы квадратная матрица A была ортогональной, необходимо и достаточно, чтобы выполнялось одно из условий: A^TA = I; AA^T = I; A^T = A^-1.

2. Определитель ортогональной матрицы равен 1.

Теорема ( о приведении действительной симметрической матрицы к диагональному виду)Пусть A - действительная симметрическая матрица (a_ij = a_ji, ). Тогда:

1. Все собственные значения матрицы A действительны;

2. Собственные векторы матрицы A, отвечающие различным собственным значениям, ортогональны;

3. Матрица A приводится к диагональному виду  с помощью ортогональной диагонализирующей матрицы S преобразованием S^TAS = , причём на диагонали матрицы  стоят собственные значения матрицы A.

Метод ортогональной матрицы приведения квадратичной формы к каноническому виду.

Пусть дана квадратичная форма Q = X^TAX. Т.к. A - симметрическая матрица, то по теореме о приведении действительной симметрической матрицы к диагональному виду для неё существует ортогональная диагонализирующая матрица S, такая, что

S^TAS =  = ,

где _i, , - собственные значения матрицы A.

Подвергнем квадратичную форму линейному преобразованию X = SY, где Y – вектор-столбец новых переменных y_i, , : Y = . Тогда Q = X^TAX = (SY)^TA(SY) = Y^TS^TASY = Y^T(S^TAS)Y = Y^TY =

= = =

= .

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Приведение квадратичной формы к нормальному виду.

Пусть квадратичная форма (1) приведена к каноническому виду где .

Совершим дополнительное преобразование переменных:

, т.е. .

Оно приведёт форму F к нормальному виду:

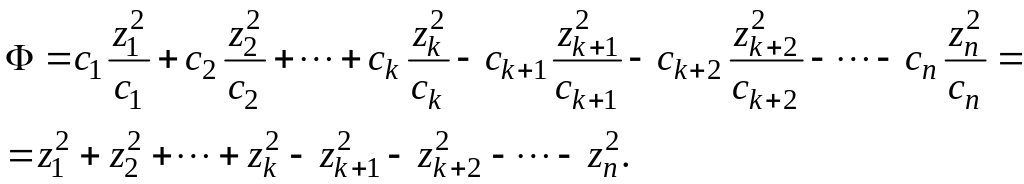
Пример. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму

и записать её в каноническом и нормальном видах.

Решение.

1. Выпишем матрицу квадратичной формы. .

2. Найдём собственные значения матрицы A. Для этого составим характеристическое уравнение . Откуда .

3. Найдём собственный вектор , отвечающий собственному значению . Для этого решим систему линейных уравнений

= ; = ;

.

Положив x₂ = 1, получим собственный вектор .

4. Найдём собственный вектор , отвечающий собственному значению . Для этого решим систему линейных уравнений

= ; = ;

. Положив x₁ = 1, получим собственный вектор .

5. Нормируя собственные векторы и , получим ортонормированные собственные векторы:

.

.

6. Ортогональная диагонализирующая матрица S, приводящая квадратичную форму к каноническому виду, будет иметь вид:

S = .

7. Применив невырожденное линейное преобразование X = SY, X = , Y = , т.е. , , получим искомый канонический вид квадратичной формы: .

8. Совершив дополнительное преобразование переменных , т.е. , получим нормальный вид квадратичной формы: .