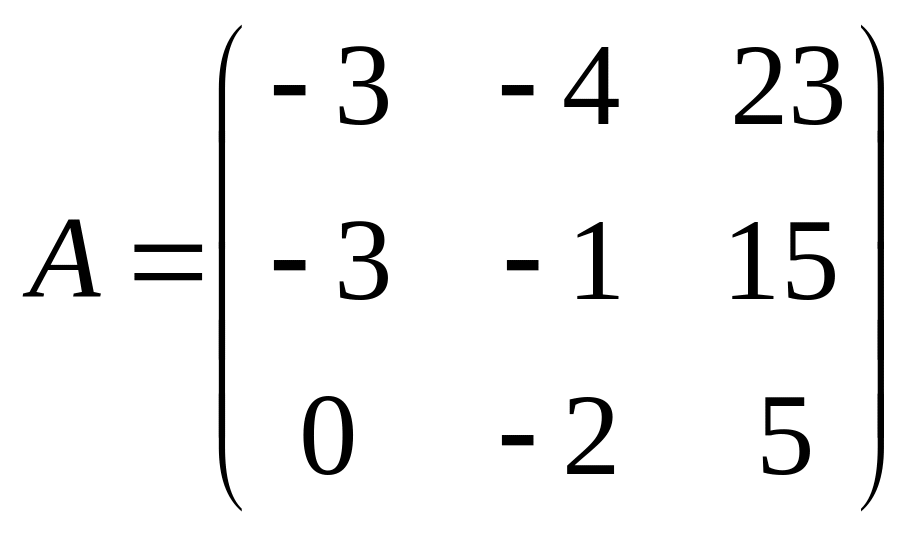- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1. Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •Линейное пространство.
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •1. Постановка задачи линейного программирования (злп)
- •2. Графический метод решения злп
- •3. Симплекс – метод решения злп
- •4. Двойственные злп
- •Методы определения опорного плана тз.
- •Вопросы для повторения.
- •Глава 6. Балансовые модели
- •1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 52
- •Глава 4. Векторная алгебра 103
- •Глава 5. Задачи линейного программирования 118
- •Глава 6. Балансовые модели 153
- •394026 Воронеж, Московский просп., 14
Линейное пространство.
Определение.
Множество
![]() называется линейным векторным
пространством, если:
называется линейным векторным
пространством, если:
1.
В
введены операция сложения элементов
т.е.
![]()
![]()
![]() элемент
элемент
![]() со свойствами:
со свойствами:
а)
![]() ;
;
б)
![]() ;
;
в)
![]()
![]() (элемент
(элемент
![]() называется нулевым);
называется нулевым);
г)
![]() :
:
![]() (элемент
(элемент
![]() называется противоположным элементу
называется противоположным элементу
![]() ).
).
2.
В
введена операция умножения элементов
на действительные числа, т.е.
![]() со свойствами:
со свойствами:
а)
![]() ;
б)
;
б)
![]() ,
,
![]() .
.
3. Операции сложения элементов и умножения на числа удовлетворяют законам:
а)
![]() ;
б)
;
б)
![]() .
.
Элементы линейного пространства называются векторами.
Формула преобразования координат при преобразовании базиса.
Пусть
![]() и
и
![]() - 2 различных базиса в линейном пространстве
.
Каждый из векторов базиса
- 2 различных базиса в линейном пространстве
.
Каждый из векторов базиса
![]() разложим по базису
разложим по базису
![]() :
:![]() ,
,
![]() .
Матрица
перехода
.
Матрица
перехода
![]() от базиса
к базису
называется матрица
от базиса
к базису
называется матрица
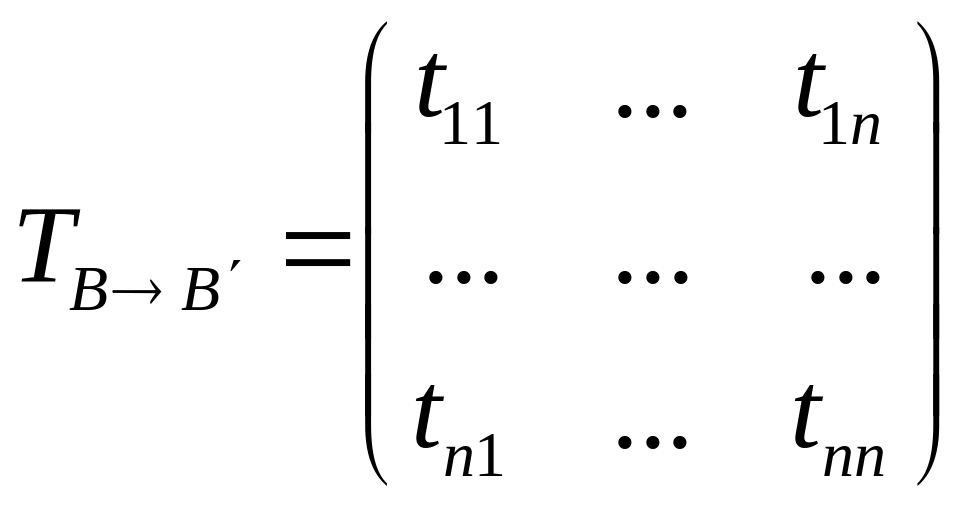 ,
,
![]() -ый
столбец которой есть вектор-столбец
-ый
столбец которой есть вектор-столбец
![]() =
=![]() ,
координат вектора
,
координат вектора
![]() в базисе
.
в базисе
.
Если
![]() - произвольный вектор из
,
- произвольный вектор из
,
![]() и
и
![]() - столбцы его координат в базисе
и
соответственно, то имеет место равенство:
- столбцы его координат в базисе
и
соответственно, то имеет место равенство:
![]() .
.
Пример.
Найти координаты вектора
в базисе
![]() ,
если он задан в базисе
,
если он задан в базисе
![]() .
.
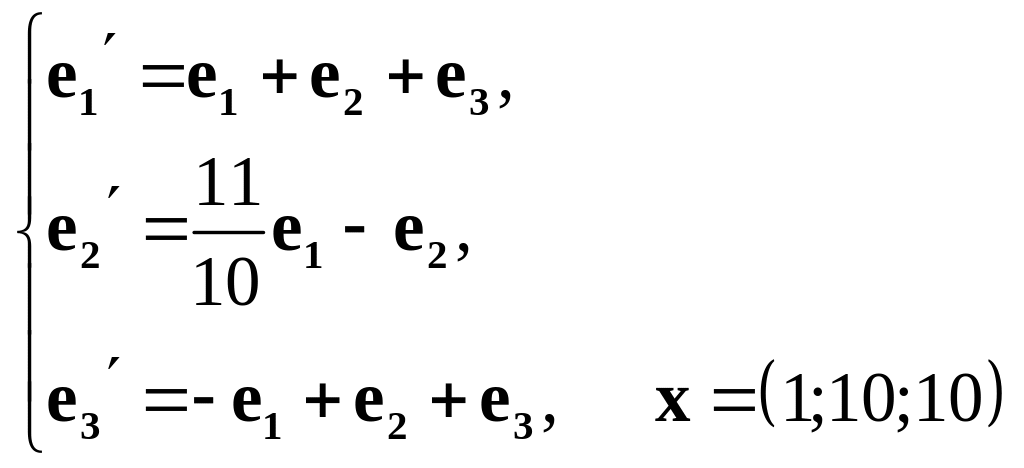
Решение. Выпишем матрицу перехода от старого базису к новому базису
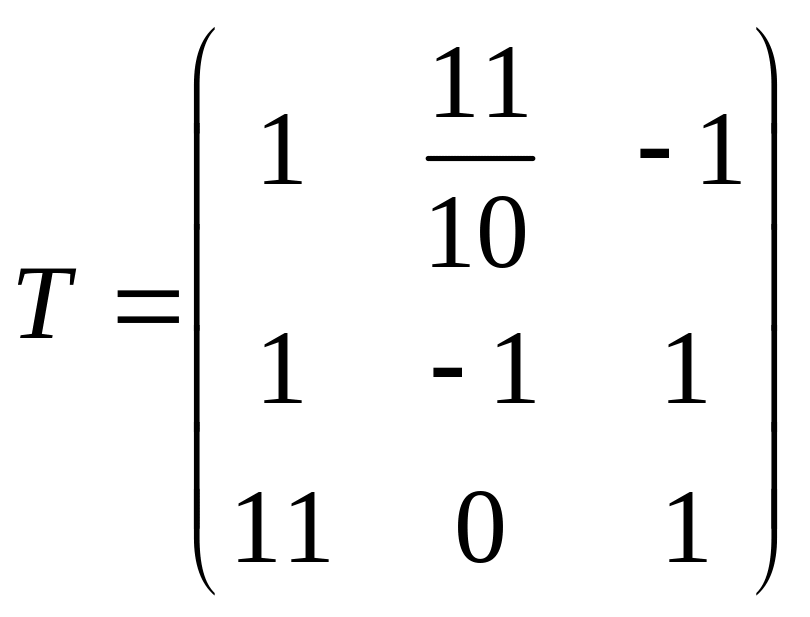
(коэффициенты
разложения векторов в новом базисе
расположены в столбцах матрицы
![]() ).
Так как определитель
).
Так как определитель
![]() матрицы отличен от нуля
матрицы отличен от нуля
![]() ,
вычислим алгебраические дополнения
элементов матрицы
:
,
вычислим алгебраические дополнения
элементов матрицы
:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Матрица
![]() ,
обратная к
,
имеет вид:
,
обратная к
,
имеет вид:
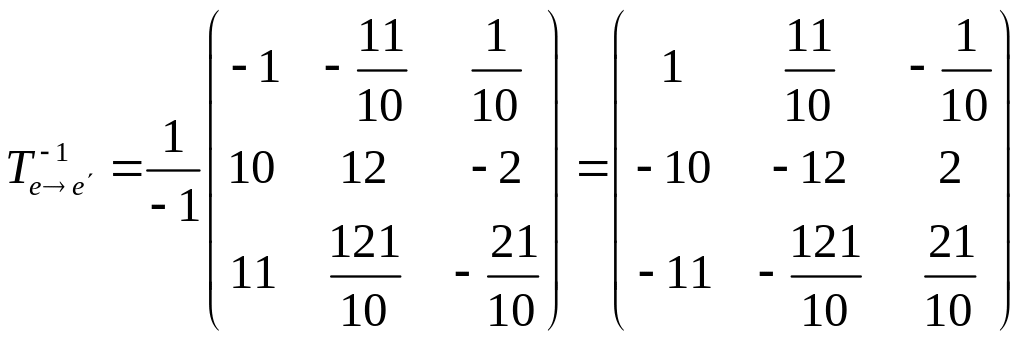 .
.
Тогда
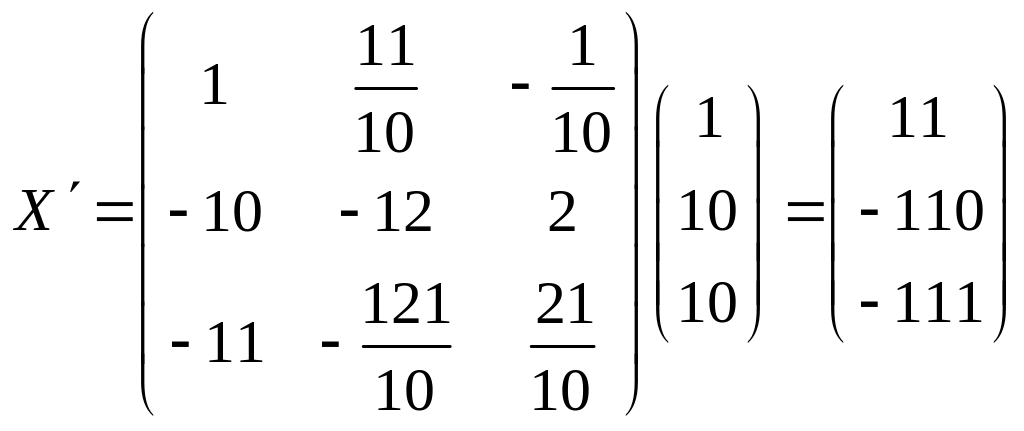 .
.
Таким
образом, координаты вектора
в базисе
![]() :
:
![]() .
.
Линейный оператор.
Определение.
Линейным
оператором
в линейном пространстве
называется всякое отображение
![]()
![]() пространства
в себя, обладающее свойствами
пространства
в себя, обладающее свойствами
![]() и
и
![]() .
.
Пример.
Пусть
![]() .
Являются ли линейным следующие
преобразования:
.
Являются ли линейным следующие
преобразования:
1)
![]()
2)
![]()
3)
![]()
Решение. 1) Проверим выполнение условий для преобразования
Имеем:![]() ;
;
![]()
![]()
Правые
части равенств не совпадают, следовательно,
![]() ,
т.е. 1- ое условие не выполнено, и
преобразование не является линейным.
,
т.е. 1- ое условие не выполнено, и
преобразование не является линейным.
2) Проверим выполнение условий для преобразования
![]() .
.
Имеем
![]() ;
;
![]()
![]() .
.
Аналогично получаем, что преобразование не является линейным
3) Проверим выполнение условий для преобразования
Имеем
![]() ;
;
![]()
![]() .
.
Первое условие выполнено.
Проверим выполнение второго условия:
![]()
Оба
условия для линейного преобразования
выполнены, следовательно преобразование
![]() является линейным.
является линейным.
Определение.
Пусть
![]() - линейный оператор в линейном пространстве
и
- некоторый фиксированный базис. Разложим
векторы
- линейный оператор в линейном пространстве
и
- некоторый фиксированный базис. Разложим
векторы
![]() ,
по базису
:
,
по базису
:
![]() ,
.
,
.
Тогда матрица
называется
матрицей
оператора
в базисе
.
Заданием матрицы оператор определяется
однозначно. Пусть
и
![]() - матрицы оператора в базисах
и
,
а
- матрицы оператора в базисах
и
,
а
![]() - матрица перехода от базиса
к базису
.Тогда
формула преобразования матрицы оператора
при преобразовании базиса имеет вид
- матрица перехода от базиса
к базису
.Тогда
формула преобразования матрицы оператора
при преобразовании базиса имеет вид
![]() .
.
Пример.
Найти матрицу
в базисе
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
если она задана в базисе
:
,
если она задана в базисе
:
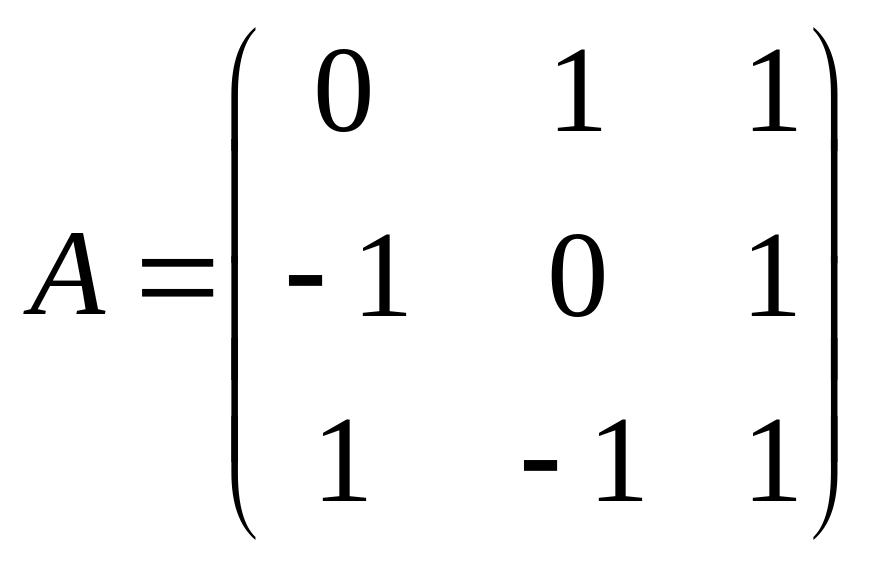 .
.
Решение.
Найдем матрицу перехода
,
записывая коэффициенты при базисе
![]() по столбцам:
по столбцам:
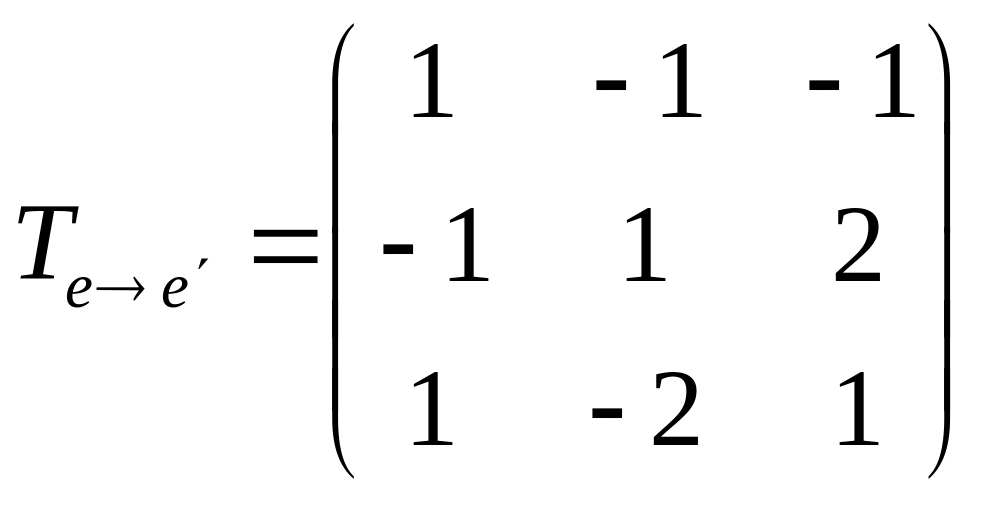 .
.
Определитель
этой матрицы:
![]() отличен от нуля, следовательно матрица
имеет обратную
.
Используя формулу для вычисления
обратной матрицы, находим
:
отличен от нуля, следовательно матрица
имеет обратную
.
Используя формулу для вычисления
обратной матрицы, находим
:
 .
.
Тогда
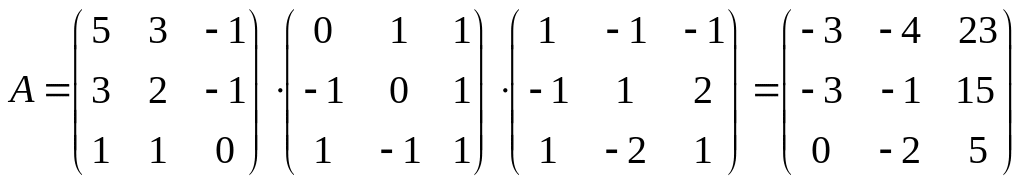 .
.
Таким
образом матрица
![]() в базисе
имеет вид:
в базисе
имеет вид: