Расчет на временную нагрузку

3.12. Выполняется расчет на ПЭВМ для построения линии влияния изгибающего момента в заданном сечении и объемлющей эпюры от действия временной нагрузки, для пролёта, в котором задано сечение. На печать при этом выдаются ординаты линии влияния изгибающего момента и объемлющей эпюры (максимальные и минимальные значения) с шагом , которые далее откладываются от базы линии влияния и базы объемлющей эпюры соответственно со своим знаком. Для окончательного построения отложенные ординаты последовательно соединяются плавными кривыми линиями.

3.13. Определяется изгибающий момент в заданном сечении от действия постоянной нагрузки загружением линии влияния по формуле

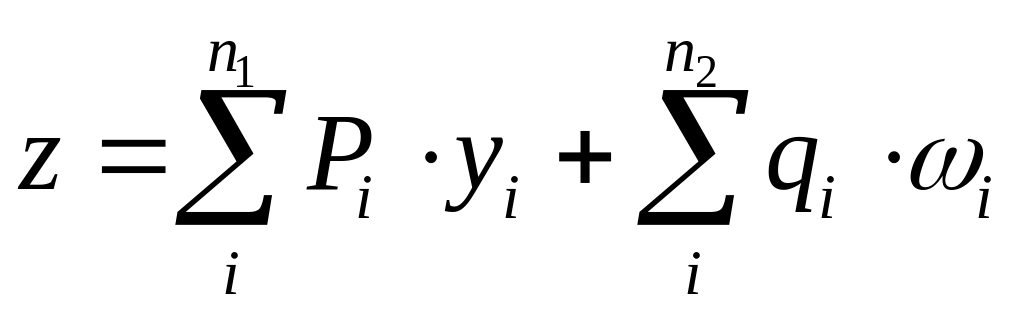, (6)

где ‑ величина сосредоточенной силы;

‑ ордината линии влияния в сечении, где приложена сосредоточенная сила;

‑ интенсивность равномерно распределенной нагрузки;

‑ площадь линии влияния под распределенной нагрузкой.

3.14. Определяется максимальный и минимальный изгибающие моменты в заданном сечении от действия временной нагрузки загружением сначала только участков линии влияния с положительными ординатами, а затем только с отрицательными ординатами. В этом случае при определении изгибающих моментов в заданном сечении загружением линии влияния от действия временной нагрузки и в формуле (6) используется только второе слагаемое формулы (6);

3.15. Заполняется таблица сравнения значений от действия постоянной и временной нагрузок, определенных непосредственным расчетом и загружением линии влияния;

3.16. Строится объемлющая эпюра от совместного действия постоянной и временной нагрузок в заданном пролете. При этом ординаты эпюры алгебраически суммируются сначала отдельно с ординатами и затем отдельно с ординатами :

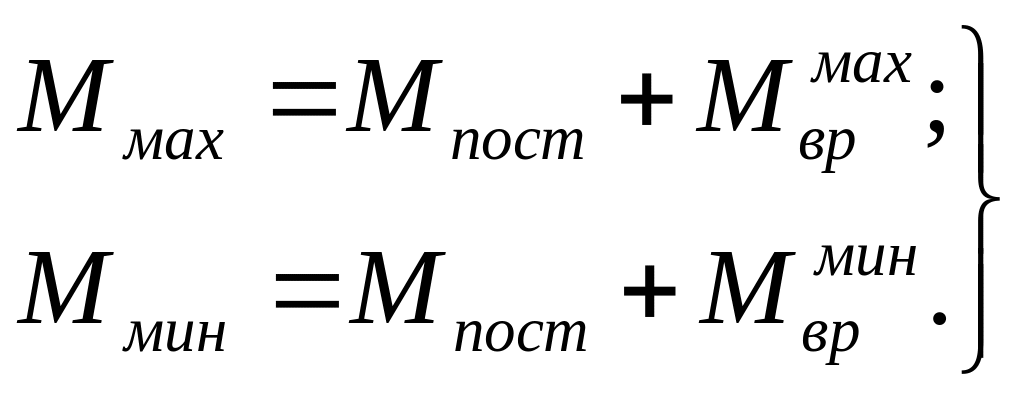(7)

4. Пример расчёта с дополнительными методическими указаниями

4.1. Задание (рис.8)

Рис. 8

4.2. Кинематический анализ

Определение числа степеней свободы (степень статической неопределимости):

;

.

Диск “балка” прикреплен к диску “земля” c помощью шести стержней непараллельных и непересекающихся в одной точке. Для их объединения достаточно трёх таких стержней. Система три раза статически неопределима и геометрически неизменяема.

4.3. Расчёт балки на действие постоянной нагрузки

4.3.1. Заданная система (р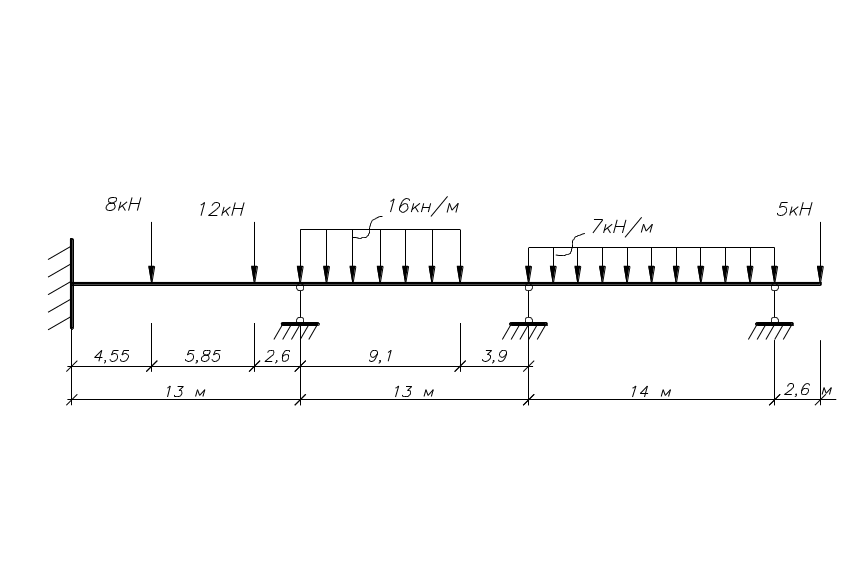ис.9)

Рис. 9

4.3.2. Основная система

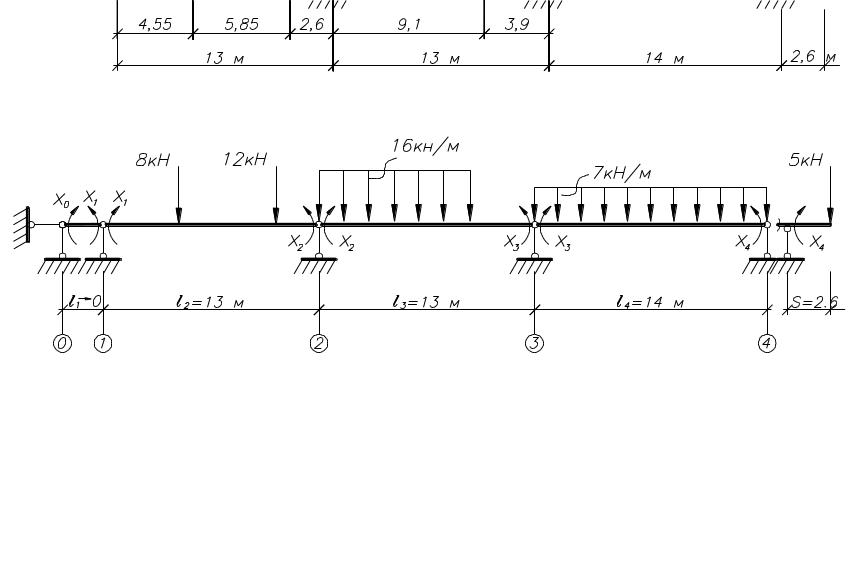Рис. 10

4.3.3. Построение эпюр поперечных сил и изгибающих моментов .

С троим эпюры поперечных сил и изгибающих моментов от действия постоянной нагрузки, при этом рассчитываем каждый пролет как отдельную балку:

Пролёт №2 (рис.11):

Проверка:

1 участок

II участок III участок

П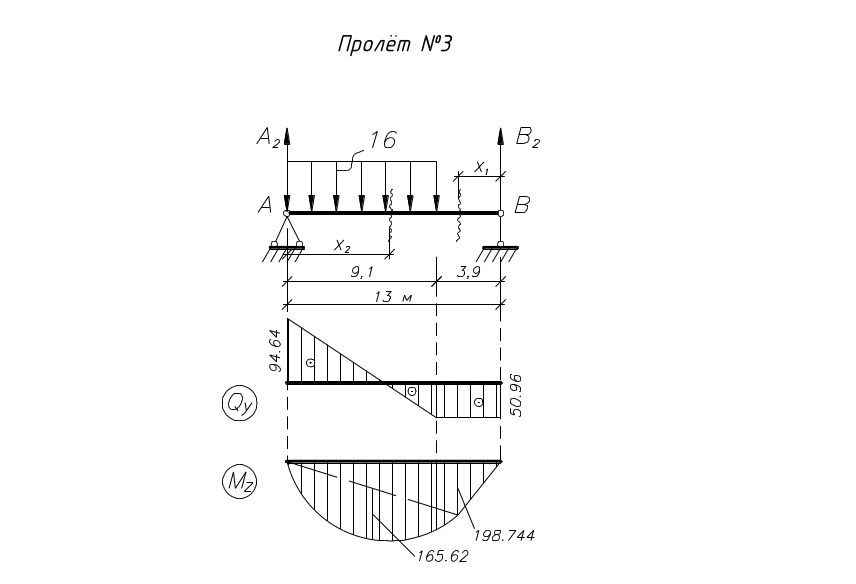 ролёт №3 (рис.12):

Проверка:

I участок

II участок

Рис.12

П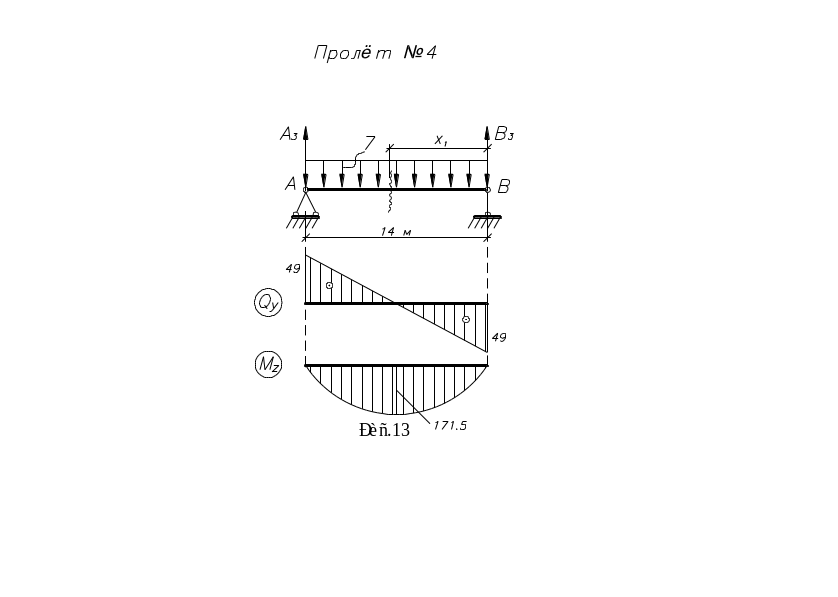 ролёт №4 (рис.13):

Проверка:

I участок

Сводные эпюры в основной системе (рис.14)

Рис. 14

4.3.4. Уравнение трёх моментов в общем виде:

.

Подставим в формулу последовательно номера неизвестных и получим

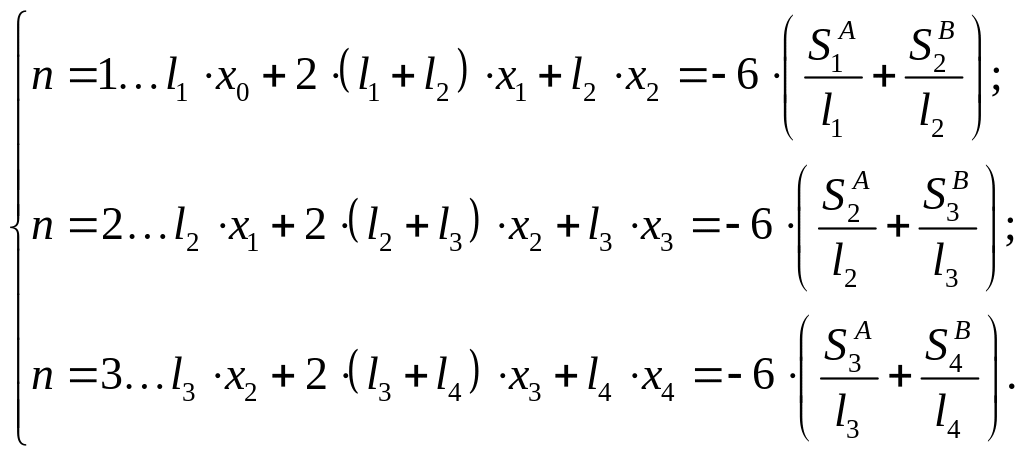
4.3.5. Определение значений статических моментов и фиктивных опорных реакций в соответствующих пролётах, входящих в правую часть уравнения трёх моментов.

;

Проверка:

Аналогичные проверки выполняются и для других пролётов.

Подставив в уравнение трёх моментов значения пролётов, фиктивных опорных реакций, известные моменты и , получим:

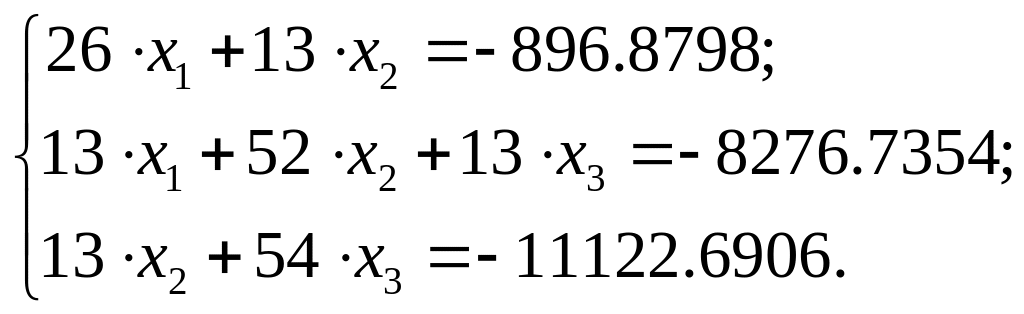
Решая систему уравнения трёх моментов, получим значения основных неизвестных:

При погрешности 0,005 допустимые невязки:

в ур.I

в ур.II

в ур.III

Действительные невязки:

Невязки допустимы.