4.2. Механический смысл производной второго порядка

Пусть материальная точка движется прямолинейно по закону . Как уже известно, производная равна скорости точки в данный момент времени: .

Покажем, что вторая производная от пути по времени есть ве­личина ускорения прямолинейного движения точки, т.е. .

Пусть в момент времени скорость точки равна , а в момент — скорость равна , т. е. за промежуток времени ско­рость изменилась на величину .

Отношение выражает среднее ускорение движения точки за время . Предел этого отношения при называется ускорением точки в данный момент и обозначается буквой : , т.е. .

Но . Поэтому , т. е. .

4.3. Производные высших порядков неявно заданной функции

Пусть функция задана неявно в виде уравнения .

Продифференцировав это уравнение по и разрешив полученное уравнение относительно , найдем производную первого порядка (первую производную). Продифференцировав по первую производную, получим вторую производную от неявной функции. В нее войдут , и .

Подставляя уже найденное значение в выражение второй произ­водной, выразим через и .

Аналогично поступаем для нахождения производной третьего (и дальше) порядка.

Пример 4.2. Найти , если .

Решение: Дифференцируем уравнение по : . Отсюда . Далее имеем: , т.е. (так как ), следовательно,

4.4. Производные высших порядков от функций, заданных параметрически

Пусть функция задана параметрическими уравнениями

Как известно, первая производная находится по формуле

. (4.1)

Найдем вторую производную от функции заданной параметриче­ски.

Из определения второй производной и равенства (4.1) следует, что

,

т.е.

. (4.2)

Аналогично получаем

, , …

Пример 4.3. Найти вторую производную функции

Решение: По формуле (4.1)

.

Тогда по формуле (23.2)

.

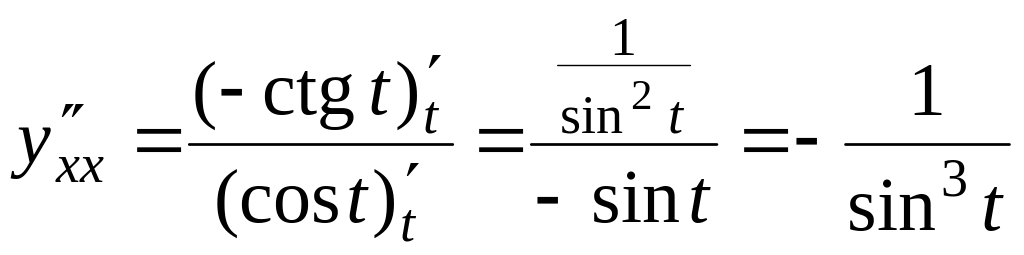Заметим, что найти можно по преобразованной формуле (4.2):

,

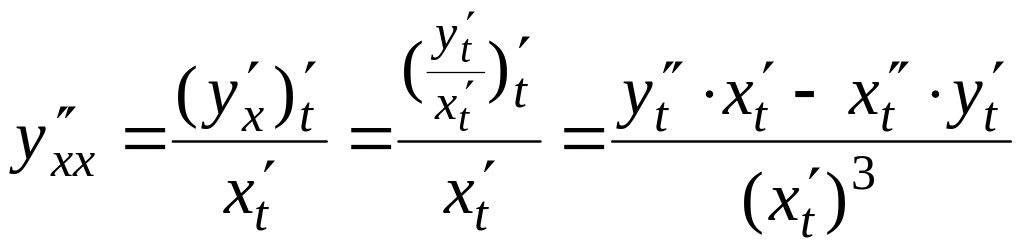запоминать которую вряд ли стоит.

§5. Дифференциал функции

5.1. Понятие дифференциала функции

Пусть функция имеет в точке отличную от нуля про­изводную . Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать , где при , или .

Таким образом, приращение функции представляет собой сум­му двух слагаемых и , являющихся бесконечно малыми при . При этом первое слагаемое есть бесконечно малая функ­ция одного порядка с , так как , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем :

.

Поэтому первое слагаемое называют главной частью приращения функции .

Дифференциалом функции в точке называется глав­ная часть ее приращения, равная произведению производной функ­ции на приращение аргумента, и обозначается (или ):

. (5.1)

Дифференциал называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной , т.е. диф­ференциал функции .

Так как , то, согласно формуле (5.1), имеем , т.е. дифференциал независимой переменной равен приращению этой переменной: .

Поэтому формулу (5.1) можно записать так:

, (5.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (5.2) следует равенство . Теперь обозна­чение производной можно рассматривать как отношение дифферен­циалов и .

Пример 5.1 . Найти дифференциал функции

.

Решение: По формуле находим

.

Пример 5.2. Найти дифференциал функции

.

Вычислить при , .

Решение:

.

Подставив и , получим

.