
- •Введение
- •§1. Производная функции
- •1.1. Задачи, приводящие к понятию производной
- •Скорость прямолинейного движения
- •Касательная к кривой
- •1.2. Определение производной; ее механический и геометрический смысл. Уравнение касательной и нормали к кривой
- •1.3. Связь между непрерывностью и дифференцируемостью функции
- •1.4. Производная суммы, разности, произведения и частного функций
- •1.5. Производная сложной и обратной функций
- •1.6. Производные основных элементарных функций Степенная функция
- •Показательная функция
- •Логарифмическая функция
- •Тригонометрические функции
- •Обратные тригонометрические функции
- •1.7. Гиперболические функции и их производные
- •1.8. Таблица производных
- •Правила дифференцирования
- •Формулы дифференцирования
- •§2. Дифференцирование неявных и параметрически заданных функций
- •2.1. Неявно заданная функция
- •2.2. Функция, заданная параметрически
- •§3. Логарифмическое дифференцирование
- •§4. Производные высших порядков
- •4.1. Производные высших порядков явно заданной функции
- •4.2. Механический смысл производной второго порядка
- •4.3. Производные высших порядков неявно заданной функции
- •4.4. Производные высших порядков от функций, заданных параметрически
- •§5. Дифференциал функции
- •5.1. Понятие дифференциала функции
- •5.2. Геометрический смысл дифференциала функции
- •5.3. Основные теоремы о дифференциалах
- •5.4. Таблица дифференциалов
- •5.5. Применение дифференциала к приближенным вычислениям
- •5.6. Дифференциалы высших порядков
- •§6. Исследование функций при помощи производных
- •6.1. Некоторые теоремы о дифференцируемых функциях
- •6.2. Правила Лопиталя
- •Раскрытие неопределенностей различных видов
- •6.3. Возрастание и убывание функций
- •6.4. Максимум и минимум функций
- •6.5. Наибольшее и наименьшее значения функции на отрезке
- •6.6. Выпуклость графика функции. Точки перегиба
- •6.7. Асимптоты графика функции
- •6.8. Общая схема исследования функции и построения графика
- •§ 7. Формула тейлора
- •7.1. Формула Тейлора для многочлена
- •7.2. Формула Тейлора для произвольной функции
- •Библиографический список
1.6. Производные основных элементарных функций Степенная функция
Степенная
функция имеет вид
![]() ,
,
![]()
Дадим
аргументу
приращение
.
Функция
получит
приращение
![]() .
По
формуле бинома Ньютона имеем
.
По
формуле бинома Ньютона имеем
 .
.
Тогда
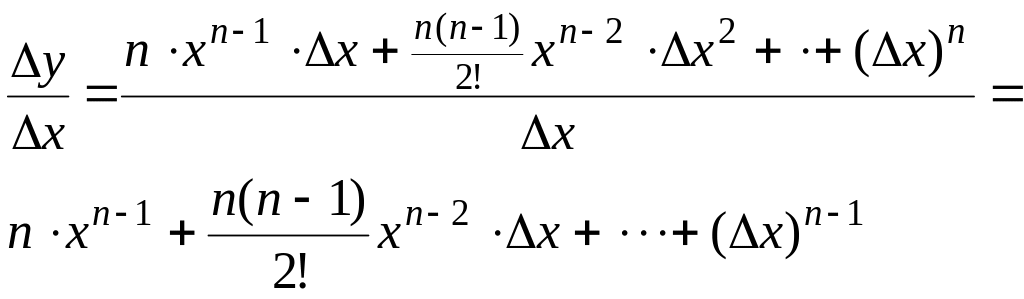 .
.
Находим предел составленного отношения при :

Таким образом,
![]() .
.
Например,
![]() ,
,
![]() ,
,
![]() .
.
Ниже
будет показано, что формула производной
степенной функции справедлива при любом
![]() (а не только натуральном).
(а не только натуральном).
Показательная функция
Показательная
функция имеет вид
![]() ,
,
![]() ,
,
![]()
Найдем
сначала производную функции
![]() .
Придав
аргументу
приращение
,
находим приращение функции
:
.
Придав
аргументу
приращение
,
находим приращение функции
:
![]() .
Следовательно,
.
Следовательно,
![]() и
и
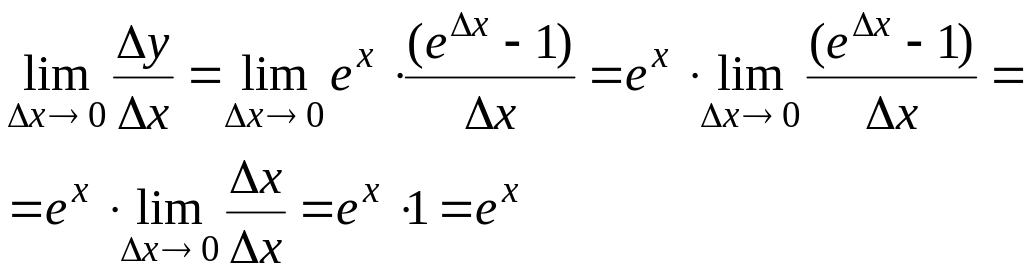 .
.
При вычислении предела воспользовались эквивалентностью
![]() при
при
![]() .
.
Итак,
![]() ,
т. е.
,
т. е.
![]() .
.
Теперь
рассмотрим функцию
,
![]() .
Так
как
.
Так
как
![]() ,
то
по формуле производной сложной функции
находим:
,
то
по формуле производной сложной функции
находим:
![]() .
.
Таким
образом,
![]() .
.
Пример
1.5. Найти
производную функции
![]() .
.
Решение: Используя формулу производной сложной функции и формулу производной показательной функции, находим
![]() .
.
Логарифмическая функция
Логарифмическая функция имеет вид
![]() ,
,
,
,
![]()
Найдем
сначала производную функции
![]() .
Для нее
.
Для нее
![]() .
.
Переходя
к пределу при
![]() и
воспользовавшись эквивалентностью
и
воспользовавшись эквивалентностью
![]() при
,
получаем:
при
,
получаем:
![]() ,
,
т.
е.
![]() или
или
![]() .
.
Теперь рассмотрим функцию .
Так
как
![]() ,
то
,
то
![]() .
.
Таким
образом,
![]() .
.
Пример
1.6. Найти
производную функции
![]() .
.
Решение:
![]() .
.
Производную
логарифмической функции
можно
найти; иначе. Так как обратной для нее
функцией является
![]() ,
то
по формуле производной обратной функции
имеем:
,
то
по формуле производной обратной функции
имеем:
![]() .
.
Тригонометрические функции
Рассмотрим
функции![]() ,
,
![]() ,
,
![]() ,
,
![]()
Для функции имеем:
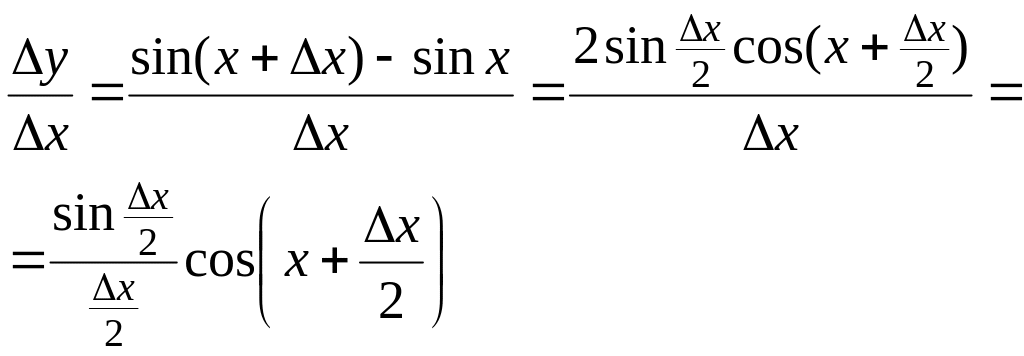 .
.
Переходя
к пределу при
и
воспользовавшись первым замечательным
пределом
![]() получаем
получаем
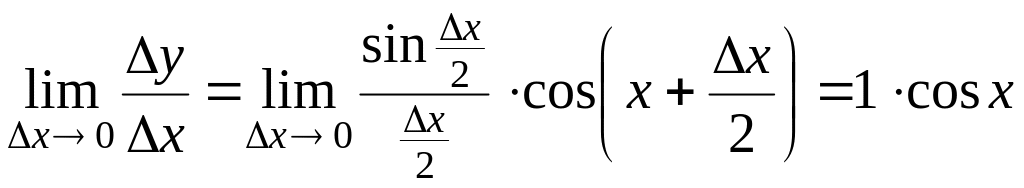 ,
,
т.е.
![]() или
или
![]() .
.
Найдем производную функции , воспользовавшись формулой производной сложной функции:
![]() ,
,
т.е.
![]() .
.
Для нахождения производных функций и воспользуемся формулой производной частного:
 ,
,
т.е.
![]() .
.
Проделав аналогичные операции, получим формулу
![]() .
.
Этот результат можно получить иначе:
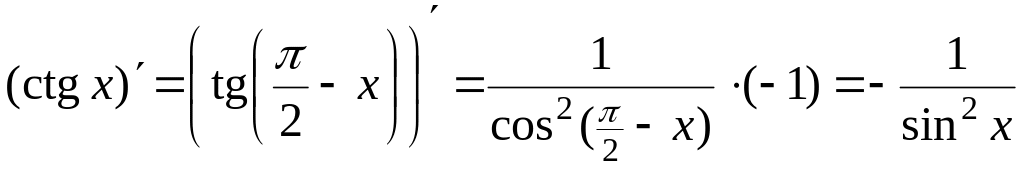 .
.
Пример
1.7. Найти
производную функции
![]() .
.
Решение:
![]() .
.
Обратные тригонометрические функции
Рассмотрим
функции![]() ,
,
![]() ,
,
![]() ,
,
![]()
Пусть
.
Обратная ей функция имеет вид
![]() ,
,
![]() .
На интервале
.
На интервале
![]() верно
равенство
верно
равенство
![]() .
.
По правилу дифференцирования обратных функций
![]() ,
,
где
перед корнем взят знак плюс, так как
![]() при
при
![]() .
.
Итак,
![]() .
.
Аналогично
получаем, что
![]() .
Эту
формулу можно получить проще: так как
.
Эту
формулу можно получить проще: так как
![]() ,
т.е.
,
т.е.
![]() ,
то
,
то
![]() .
.
Найдем производную функции .
Она
является обратной к функции
![]() ,
где
.
,
где
.
Поэтому, по правилу дифференцирования обратных функций, пот] л у чаем, что
![]() .
.
Итак,
![]() .
.
Функции и связаны отношением
![]() ,
т.е.
,
т.е.
![]() .
.
Дифференцируя это равенство, находим
![]() ,
,
т.е.
![]() .
.
Пример
1.8. Найти
производные функций: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
Решение:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() .
.
Замечание:
Найдем
производную степенной функции
![]() с любым показателем
с любым показателем
![]() .
В этом случае функция рассматривается
для
.
В этом случае функция рассматривается
для
![]() .
.
Можно
записать
![]() .
По правилу дифференцирования сложной
функции находим
.
По правилу дифференцирования сложной
функции находим
 ,
,
т.е.
![]() .
.
Формула
остается справедливой и для
![]() ,
если функция
существует:
,
если функция
существует:
![]() .
.
при
всех
![]() .
.
Пример
1.9. Показать,
что функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
Решение:
Находим
![]() :
:
![]() ,
,
т.е.
![]() .
Подставляем значение
в
данное уравнение:
.
Подставляем значение
в
данное уравнение:
![]() ,
т. е.
,
т. е.
![]() ,
0 = 0.
,
0 = 0.
Функция удовлетворяет данному уравнению.
