1.4. Производная суммы, разности, произведения и частного функций

Нахождение производной функции непосредственно по определе­нию часто связано с определенными трудностями. На практике функ­ции дифференцируют с помощью ряда правил и формул.

Пусть функции и – две дифференцируемые в некотором интервале функции.

Теорема 1.2. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: .

Доказательство. Обозначим . По определению производной и основным теоремам о пределах получаем:

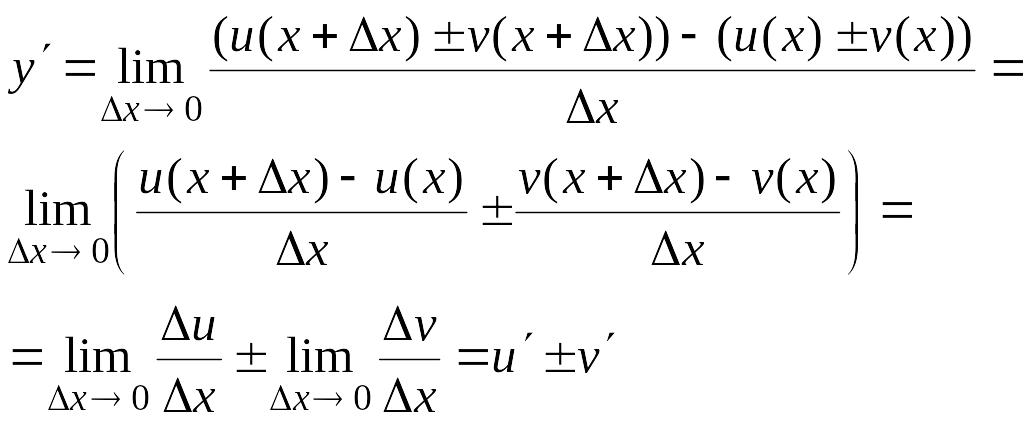
т.е. .

Теорема справедлива для любого конечного числа слагаемых.

Теорема 1.3. Производная произведения двух функций равна произ­ведению производной первого сомножителя на второй плюс произве­дение первого сомножителя на производную второго: .

Доказательство. Пусть . Тогда

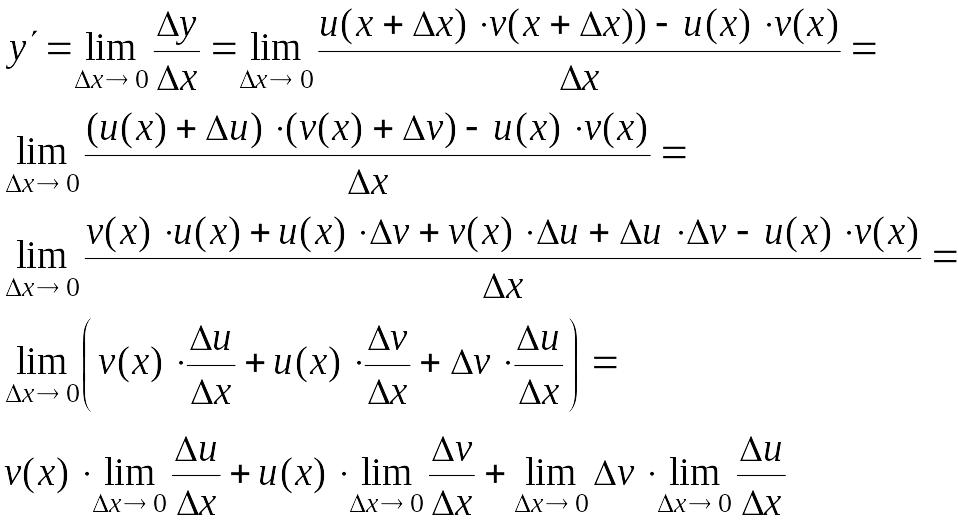
т. е. .

При доказательстве теоремы использовалась теорема о связи не­прерывности и дифференцируемости: так как функции и дифференцируемы, то они и непрерывны, поэтому и при .

Можно показать, что:

а) , где = const;

б) .

Теорема 1.4. Производная частного двух функций , если равна дроби, числитель которой есть разность произведений зна­менателя дроби на производную числителя и числителя дроби на про­изводную знаменателя, а знаменатель есть квадрат прежнего знаменателя: , .

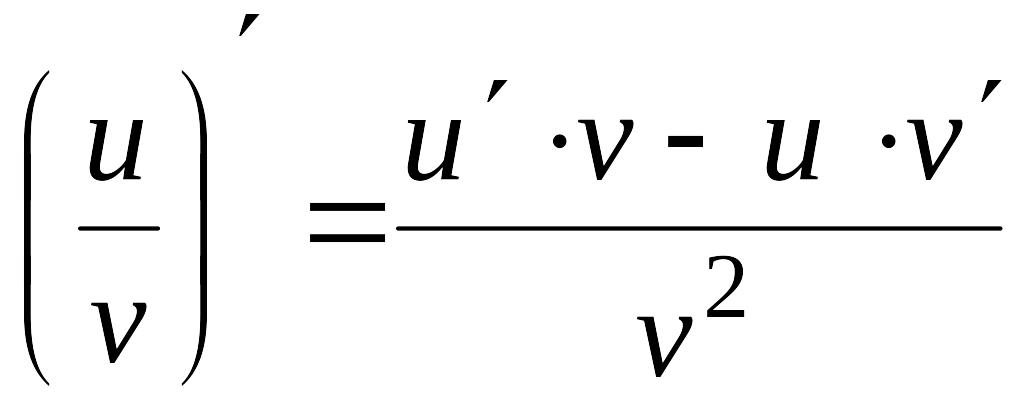Доказательство. Пусть . Тогда

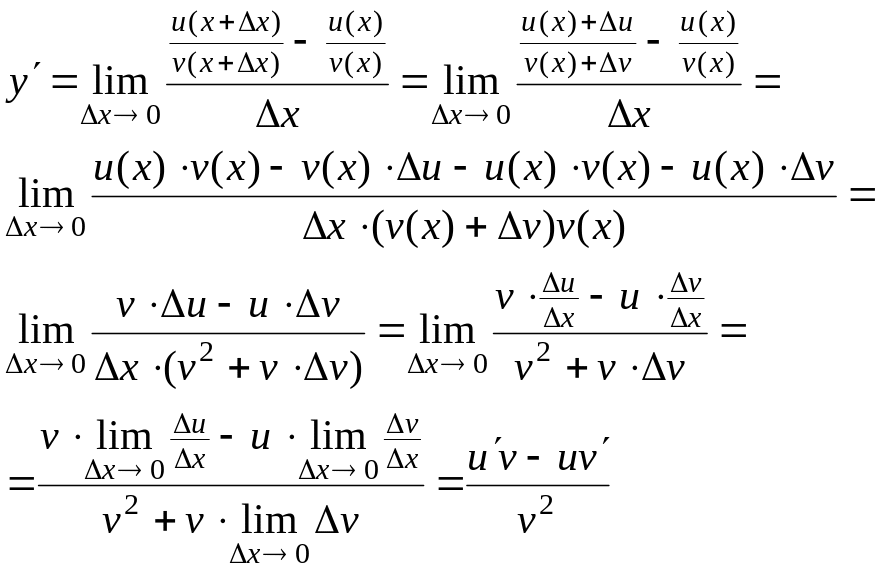
т.е. .

Следствие 1.1. .

Следствие 1.2. , где = const.

1.5. Производная сложной и обратной функций

Пусть и , тогда — сложная функция с промежуточным аргументом и независимым аргументом .

Теорема 1.5. Если функция имеет производную в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке , которая находится по формуле .

Доказательство. По условию . Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем или

, (1.6)

где при .

Функция имеет производную в точке : , поэтому

, где при .

Подставив значение в равенство (1.6), получим

,

т. е.

.

Разделив полученное равенство на и перейдя к пределу при , получим .

Итак, для нахождения производной сложной функции надо произ­водную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Это правило остается в силе, если промежуточных аргументов не­сколько. Так, если , , , то . Пусть и — взаимно обратные функции.

Теорема 1.6. Если функция строго монотонна на интер­вале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также име­ет производную в соответствующей точке, определяемую равен­ством или .

Доказательство. Рассмотрим обратную функцию . Дадим аргументу приращение . Ему соответствует приращение обратной функции, причем Дж в силу строгой монотонности функции . Поэто­му можно записать

(1.7)

Если , то в силу непрерывности обратной функции приращение . И так как , то из (1.7) следуют равенства , т.е. .

Таким образом, производная обратной функции равна обратной величине производной данной функции.

Правило дифференцирования обратной функции записывают так:

или .

Пример 1.3. Найти производную функции .

Решение: Данная функция является сложной. Ее можно предста­вить в виде цепочки «простых» функций: , где , где , где . По правилу дифференцирования сложной функ­ции ( ) получаем:

.

Пример 1.4. Пользуясь правилом дифференцирования обрат­ной функции, найти производную для функции .

Решение: Обратная функция имеет производную . Следовательно,

.