6.2. Правила Лопиталя
Рассмотрим
способ раскрытия неопределенностей
вида
и
который
основан на применении производных.
Теорема
6.4 (Правило Лопиталя раскрытия
неопределенностей вида
).
Пусть функции
и
непрерывны
и дифференцируемы в окрестности
точки
и
обращаются в нуль в этой точке:
.
Пусть
в
окрестности точки
.
Если
существует предел
,
то
.
Доказательство.
Применим
к функциям
и
теорему
Коши для отрезка
,
лежащего
в окрестности точки
.
Тогда
,
где
лежит
между
и
(рис.
6.4). Учитывая, что
,
получаем
.
При
,
величина
с также стремится к
;
перейдем
в равенстве (6.4) к пределу:
.
Так
как
,
то
.
Поэтому
.
Коротко полученную формулу читают так: предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует.
Замечания:
1.
Теорема 6.4 верна и в случае, когда функции
и
не
определены при
,
но
и
.
Достаточно положить
и
.
2.
Теорема 6.4 справедлива и в том случае,
когда
.
Действительно, положив
,
получим
.
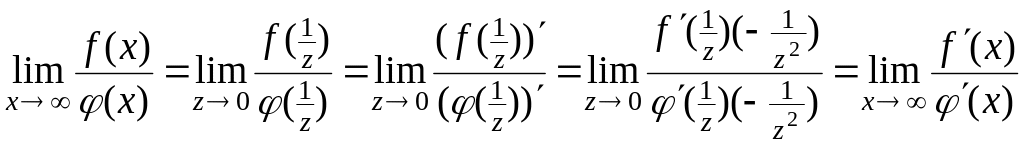3.
Если производные
и
удовлетворяют
тем же условиям, что и функции
и
,
теорему
6.4 можно применить еще раз:
и т. д.
Пример
6.2. Найти
.
Решение:
.
Пример
6.3. Найти
.
Решение:
.
Теорема 6.4 дает возможность раскрывать неопределенность вида . Сформулируем без доказательства теорему о раскрытии неопределенности вида .
Теорема
6.5 (Правило Лопиталя раскрытия
неопределенностей
).
Пусть
функции
и
непрерывны
и дифференцируемы в окрестности
точки
(кроме, может быть, точки
),
в
этой окрестности
,
.
Если
существует предел
,
то
. (6.4)
Пример
6.4.
Найти
.
Решение:
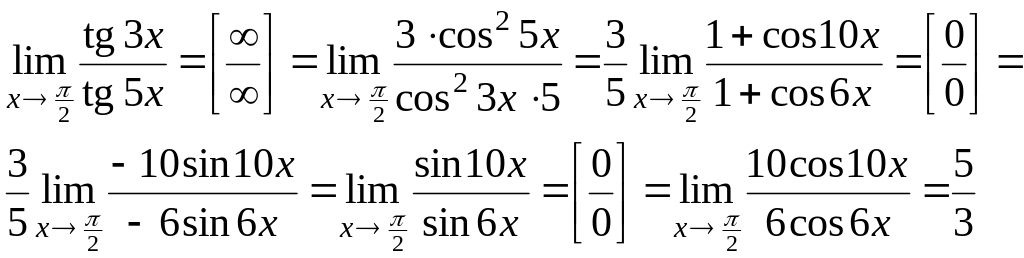
2-й способ:
.
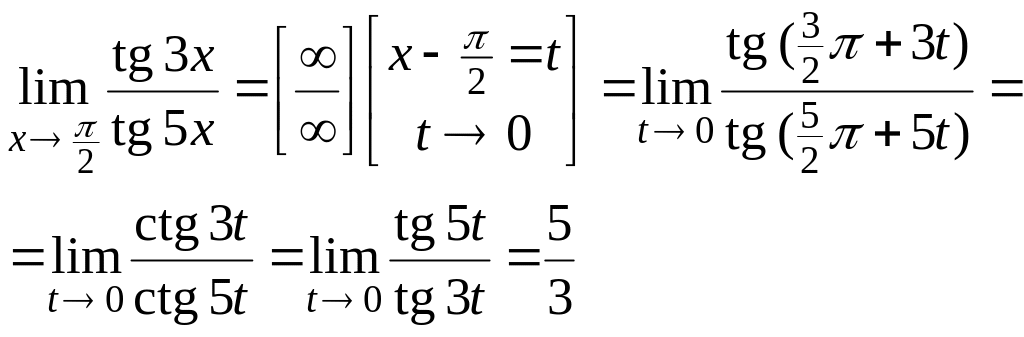Раскрытие неопределенностей различных видов
Правило
Лопиталя применяется для раскрытия
неопределенностей вида
и
,
которые называют основными.
Неопределенности
вида
,
,
,
,
сводятся к двум основным видам путем
тождественных преобразований.
Пусть
,
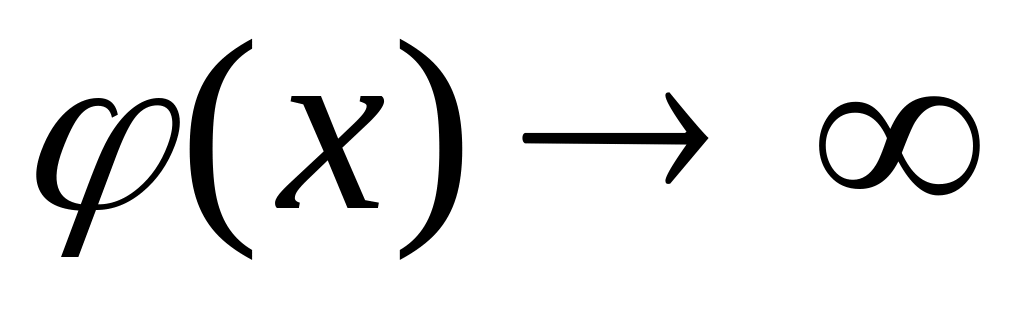при
.
Тогда очевидны следующие преобразования:
.
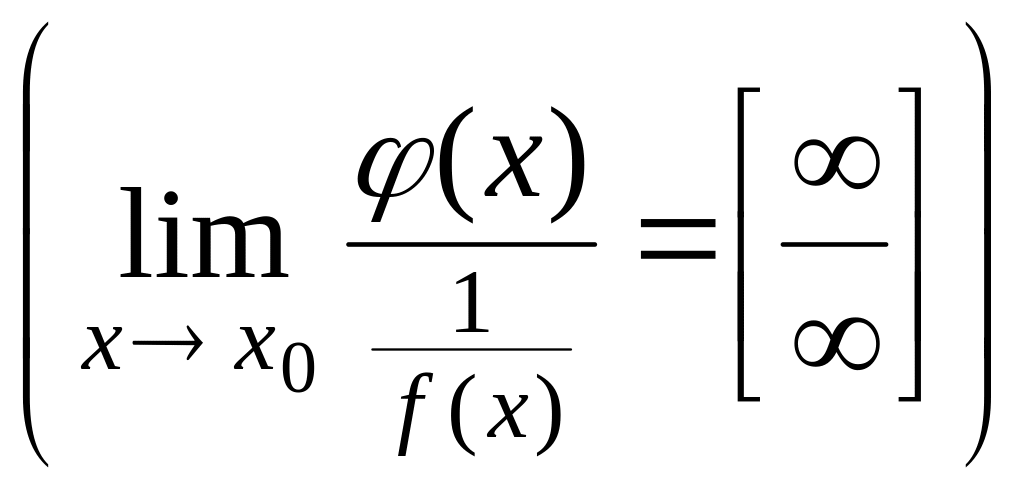Например:
.
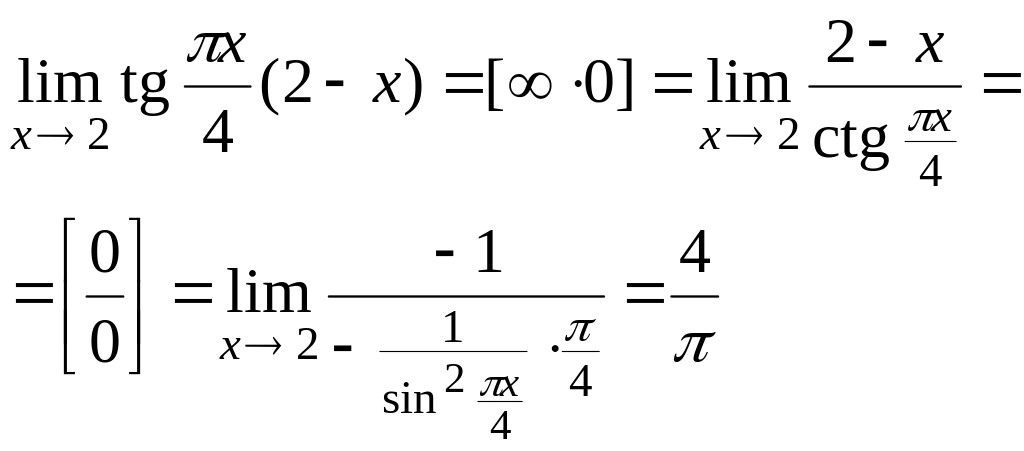Пусть
,
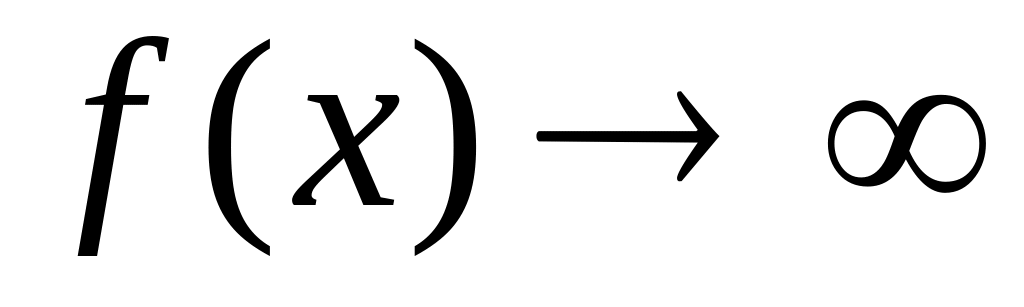при
.
Тогда можно поступить так:
.
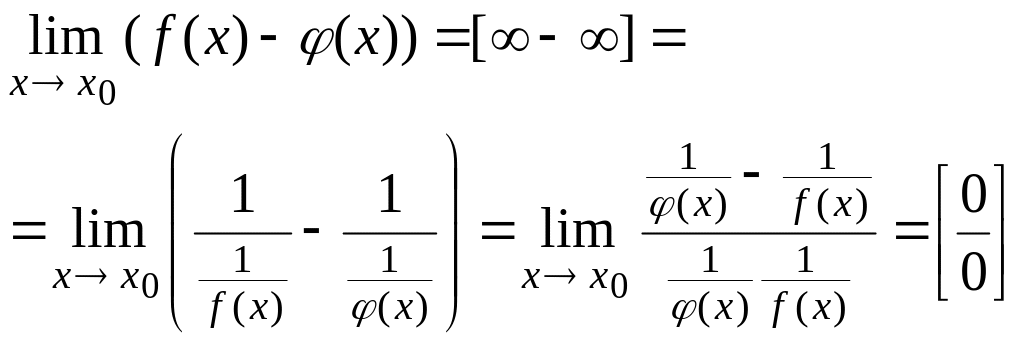На практике бывает проще, например,
Пусть ил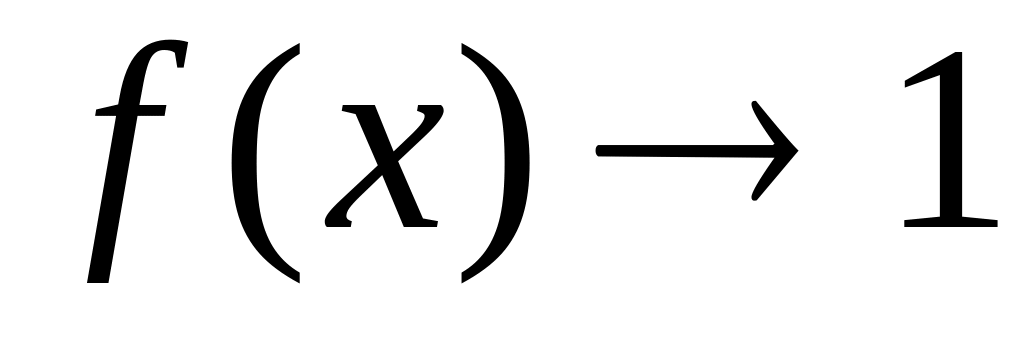и
и
,
или
и
,
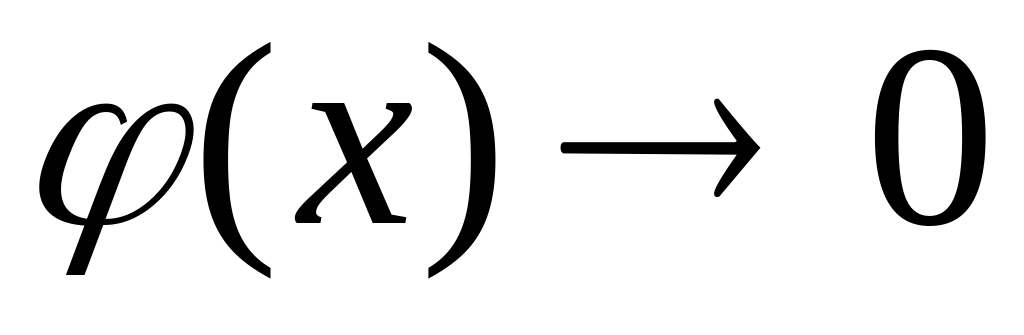или
и
при
.
Для
нахождения предела вида
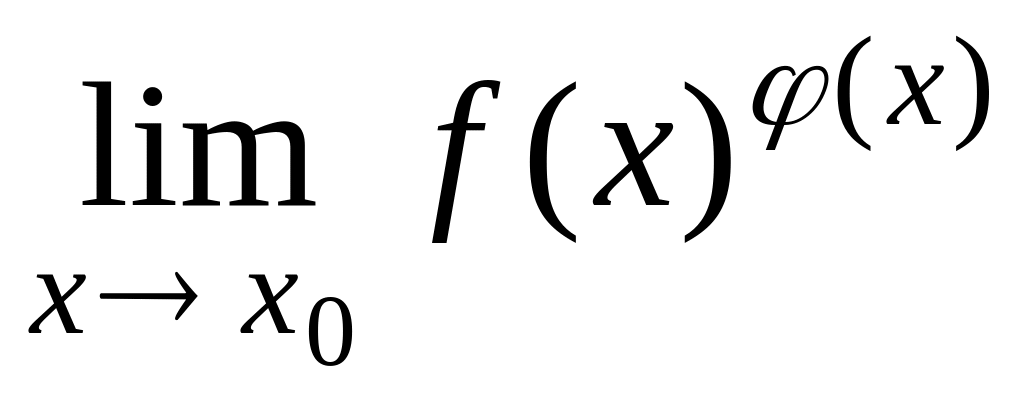удобно
сначала прологарифмировать выражение
.
Пример
6.5. Найти
.
Решение:
Имеем неопределенность вида
.
Логарифмируем выражение
,
получим:
.
Затем находим предел:
,
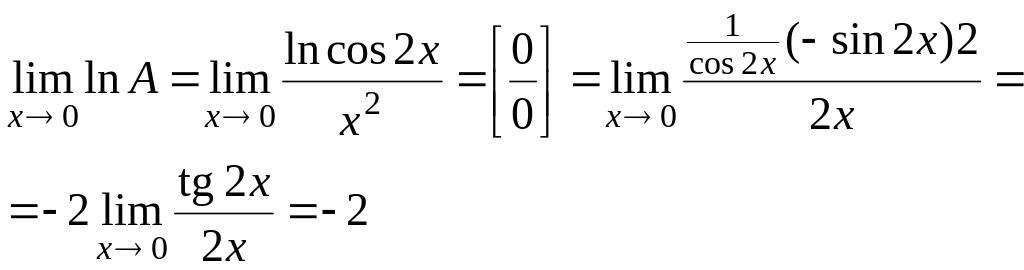т.е.
.
Отсюда
,
и
.
Решение можно оформить короче, если воспользоваться «готовой» формулой
(использовано
основное логарифмическое тождество:
).
Пример
6.6. Найти
.
Решение:
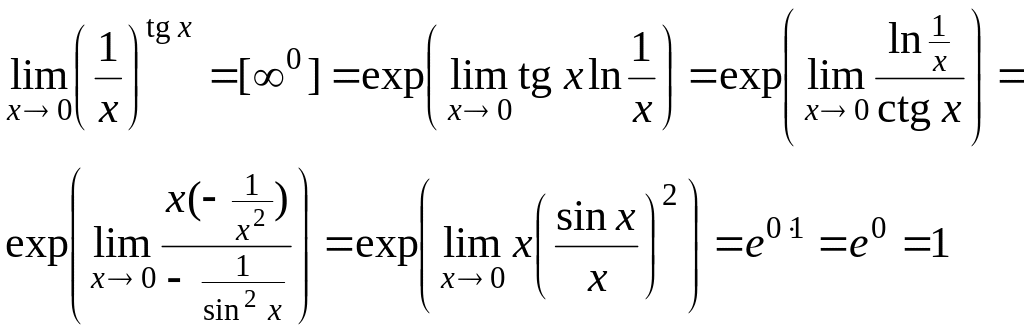
Пример 6.7. Пусть
Найти
.
(Дополнительно: найти
.)
Решение: При имеем
.
При
по определению производной:
.
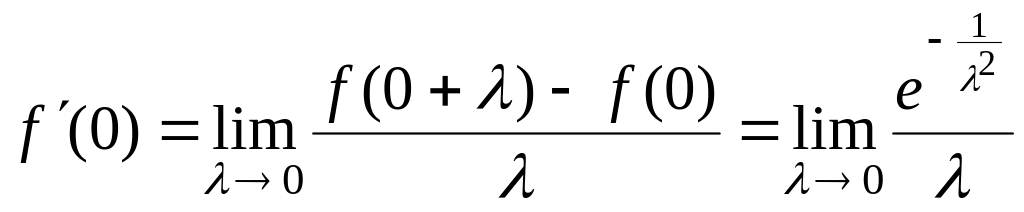Делаем
замену
и применяем правило Лопиталя
.
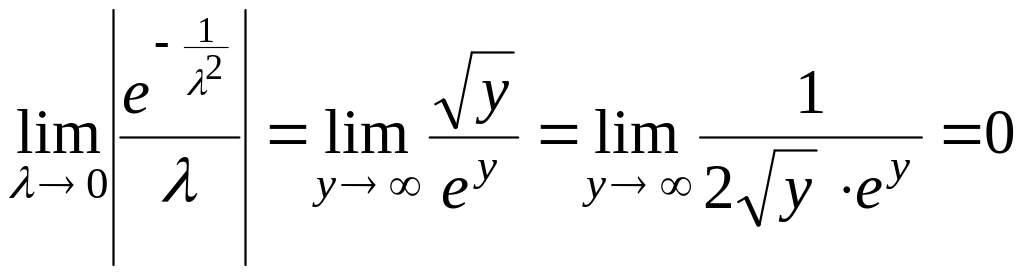Таким образом,
.
Аналогично
можно показать, что
.
6.3. Возрастание и убывание функций
Одним из приложений производной является ее применение к исследованию функций и построению графика функции.
Установим необходимые и достаточные условия возрастания и убывания функции.
Теорема
6.6 (необходимые условия). Если
дифференцируемая на интервале
функция
возрастает
(убывает), то
(
)
для
.
Доказательство.
Пусть функция
возрастает
на интервале
.
Возьмем
произвольные точки
и
на интервале
и
рассмотрим отношение
.
Функция
возрастает, поэтому если
,
то
и
;
если
,
то
и
.
В обоих случаях
.
В обоих случаях
,
так числитель
и знаменатель дроби имеют одинаковые
знаки. По условию теоремы функция
имеет производную в точке
и
является пределом рассматриваемого
отношения. Следовательно,
.
Аналогично рассматривается случай, когда функция убывает на интервале .
Геометрически теорема 6.6 означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси или в некоторых точках (на рисунке 6.5 в точке с абсциссой ) параллельны оси .
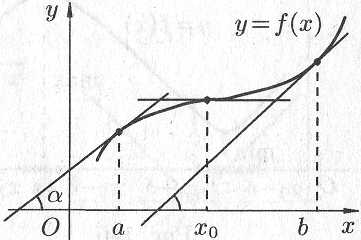
Рис. 6.5
Теорема
6.7 (достаточные условия). Если
функция
дифференцируема на интервале
и
для
,
то эта функция возрастает (убывает) на
интервале
.
Доказательство.
Пусть
.
Возьмем точки
и
из
интервала
,
причем
.
Применим
к отрезку
теорему
Лагранжа:
,
где
.
По условию
,
.
Следовательно
или
,
т.е.
функция
на
интервале
возрастает.
Рассмотренные теоремы 6.6 и 6.7 позволяют довольно просто исследовать функцию на монотонность. Напомним, что функция возрастающая или убывающая называется монотонной .
Пример
6.8. Исследовать
функцию
на возрастание и убывание.
Решение:
Функция определена на
.
Ее производная равна:
;
при
;
при
.
Ответ:
данная функция возрастает на интервалах
и
;
убывает на интервале
.