Введение

Математика – самая древняя и в то же время самая юная из наук. Она складывалась во втором тысячелетии до нашей эры, когда потребности торговли, землемерия и мореплавания заставили упорядочить приемы счета и измерения, начало которых уходит в еще более глубокую древность. Уже строители египетских пирамид владели математическими знаниями. Сложившись, математика не переставала развиваться, разрабатывались новые методы, открывались новые области, совершенствовалась символика и научный аппарат. Многие открытия в огромной степени создали возможность, как для собственного развития, так и для развития других наук, таких, как физика и астрономии.

До сих пор математика продолжает развиваться, поражая воображение многообразием специальных областей, новизной и необычностью используемых представлений и понятий, неожиданным своеобразием методов, особенностями языка. Сила математики в её способности создавать все более высокие абстракции, оперировать ими и изучать их особенности и закономерности. Именно поэтому математические методы можно применять в различных науках помимо физики по мере того, как они сами становятся теоретическими.

В данном учебном пособии излагаются основы высшей математики, поэтому он будет полезен для студентов первого курса заочной формы обучения. Авторы стремились изложить материал по возможности полно. В учебном пособии изложен и теоретический материал, и идет подробное решение типовых заданий.

§1. Производная функции

1.1. Задачи, приводящие к понятию производной

Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости разных процессов.

Скорость прямолинейного движения

Пусть материальная точка (некоторое тело) движется нерав­номерно по некоторой прямой. Каждому значению времени соответ­ствует определенное расстояние до некоторой фиксированной точки . Это расстояние зависит от истекшего времени , т. е. .

Это равенство называют законом движения точки. Требуется най­ти скорость движения точки.

Е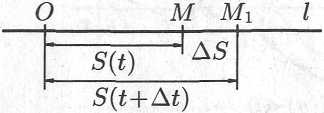 сли в некоторый момент времени точка занимает положение , то в момент времени ( — приращение времени) точка займет

Рис. 1.1

положение , где ( — приращение расстояния) (см. рис. 1.1). Таким образом, перемеще­ние точки за время будет .

Отношение выражает среднюю скорость движения точки за время :

.

Средняя скорость зависит от значения : чем меньше , тем точнее средняя скорость выражает скорость движения точки в данный момент времени .

Предел средней скорости движения при стремлении к нулю промежутка времени называется скоростью движения точки в данный момент времени (или мгновенной скоростью). Обозначив эту скорость через , получим

, или (1.1)

Касательная к кривой

Дадим сначала общее определение касательной к кривой.

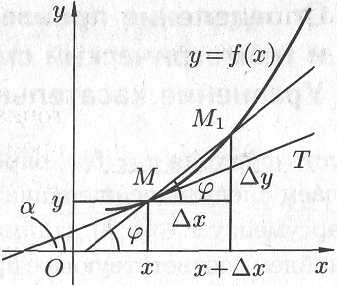
Рис. 1.2

Возьмем на непрерывной кривой две точки и (см. рис. 1.2).

Прямую , проходящую через эти точки, называют секущей.

Пусть точка , двигаясь вдоль кривой , неограниченно прибли­жается к точке . Тогда секущая, поворачиваясь около точки , стре­мится к некоторому предельному положению .

Касательной к данной кривой в данной точке называ­ется предельное положение секущей , проходящей через точку , когда вторая точка пересечения неограниченно прибли­жается по кривой к точке .

Рассмотрим теперь график непрерывной кривой , имею­щий в точке невертикальную касательную. Найдем ее угловой коэффициент , где — угол касательной с осью .

Для этого проведем через точку и точку графика с абсцис­сой секущую (см. рис. 129). Обозначим через — угол между секущей и осью . На рисунке видно, что угловой коэффициент секущей равен

.

При в силу непрерывности функции приращение тоже стремится к нулю; поэтому точка неограниченно приближается по кривой к точке , а секущая , поворачиваясь около точки , переходит в касательную. Угол , т. е. .

Следовательно, .

Поэтому угловой коэффициент касательной равен

. (1.2)

Рис. 1.3

К нахождению пределов вида (1.1) и (1.2) приводят решения и множества других задач. Можно показать, что:

– если — количество электричества, проходящего через поперечное сечение проводника за время , то сила тока в момент времени равна

;

– если — количество вещества, вступающего в химиче­скую реакцию за время , то скорость химической реакции в момент времени равна

; (1.3)

– если — масса неоднородного стержня между точками и , то линейная плотность стержня в точке есть

. (1.4)

Пределы (1.1)–(1.4) имеют одинаковый вид; везде требуется най­ти предел отношения приращения функции к приращению аргумента. Этот предел называют производной. Эти пределы можно записать так:

; ; ; ;

(читается « равно штрих по », «тангенс равен штрих по » и т. д.).