2. Вычисление длины дуги

Линия (L) в пространстве называется гладкой, если в каждой точке (L) можно провести касательную к этой линии. Если линия без самопересечений задана параметрическими уравнениями

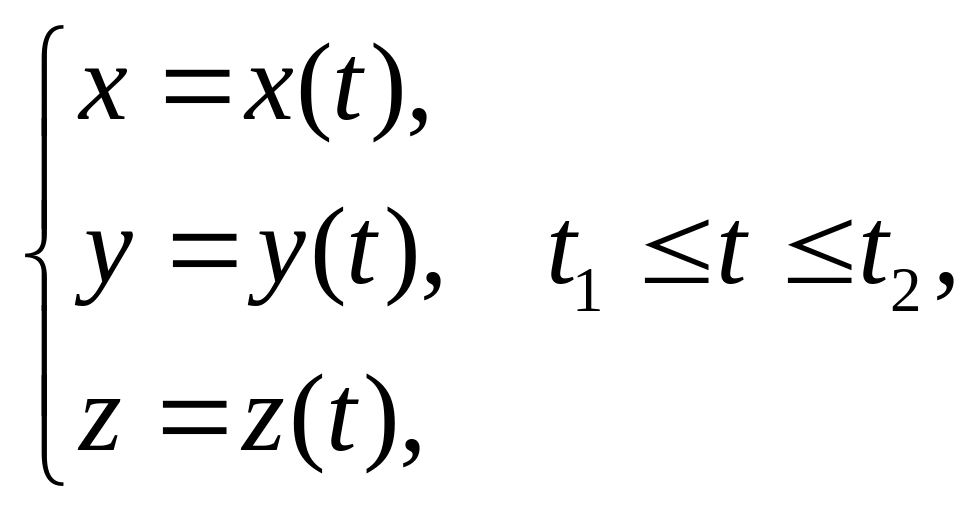
то дифференцируемость x(t), y(t), z(t) гарантирует гладкость линии; аналогичное утверждение справедливо для плоской линии. Если линия без самопересечений на плоскости с заданной полярной системой координат определена полярным уравнением , то и в этом случае дифференцируемость влечёт гладкость этой линии.

Если гладкая линия (L) на плоскости (в пространстве) задана параметрическими уравнениями x = x(t), y = y(t) (и вдобавок к этим z = z(t) для линии в пространстве), , то длина линии (L) находится по формуле

( ).

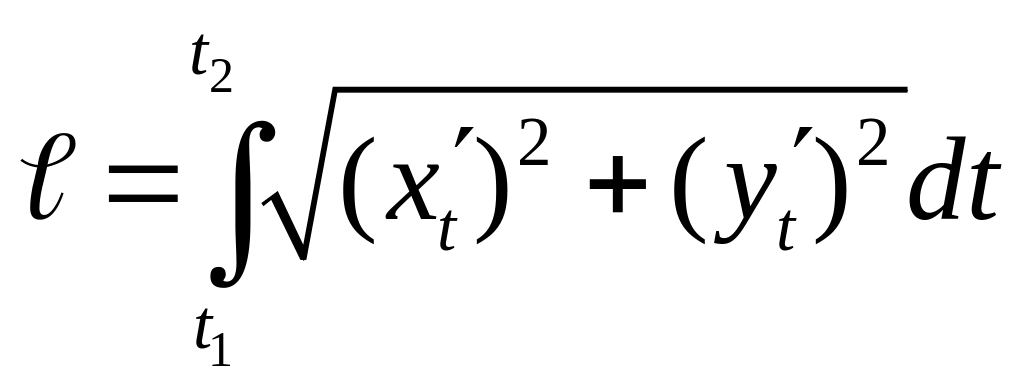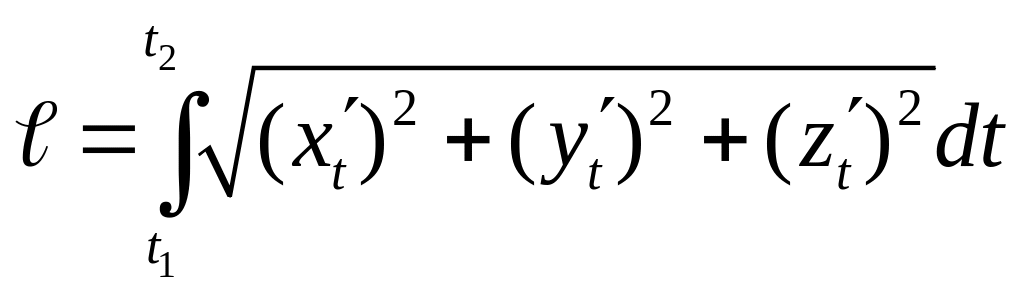Если гладкая линия (L) задана явным уравнением y = f(x) , a  x  b,то .

Для гладкой линии (L), заданной полярным уравнениями , .

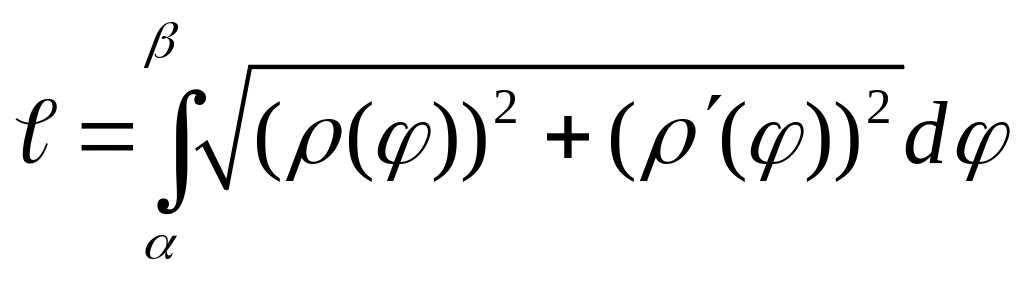Пример 31. Найти длину линии, заданной уравнением , , .

Решение. Имеем

.

Пример 32. Найти длину дуги логарифмической спирали , находящейся внутри окружности .

Решение. Дуге спирали, лежащей внутри окружности , соответствуют значения . Поэтому

.

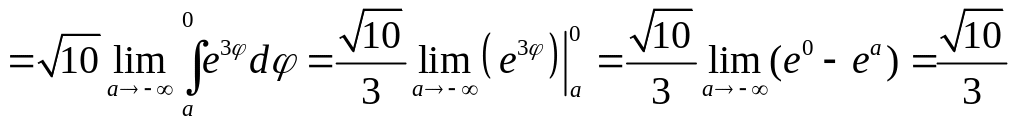3. Вычисление объёмов тел

Если в пространстве заданы ось 0х, тело (Т), проекцией которого на 0х является отрезок [a; b] , и для любого x  [a; b] известна площадь S(x) поперечного сечения S(x), то объём V тела (Т) находится по формуле .

В частности, если тело (Т) получено путём вращения графика функции , вокруг оси 0х, то объём тела вращения равен .

При вращении графика функции f(x) вокруг оси 0у формула объёма прини-

Рис.7. мает вид

.

Пример 33. Найти объём V тела (Т), ограниченного эллипсоидом

.

Решение. Проекцией тела (Т) на ось 0х является отрезок

[–a; a]. Найдём формулу площади S(x) поперечного сечения, x  [a; b]. Перепишем уравнение эллипсоида в виде

.

Это есть уравнение поперечного сечения эллипсоида плоскостью, проходящей через точку x и перпендикулярной оси 0х. А мы уже знаем (задача 27), что площадь фигуры, заключённой внутри этого эллипса, равна . Следовательно,

.

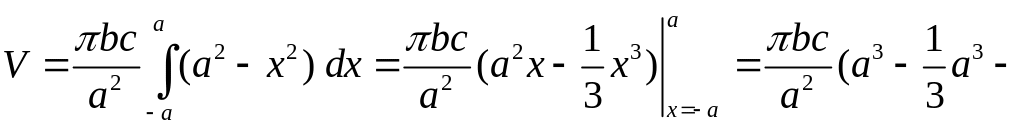
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ

Задание 1.

Найдите интегралы.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. 

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. ;

29. ;

30. .

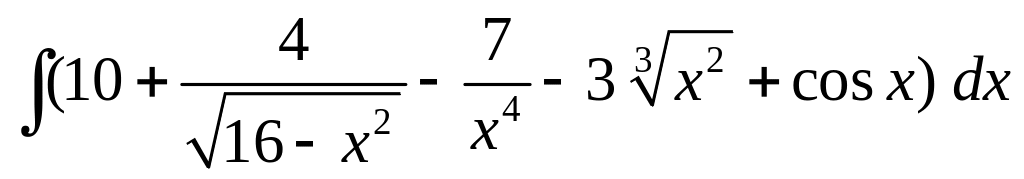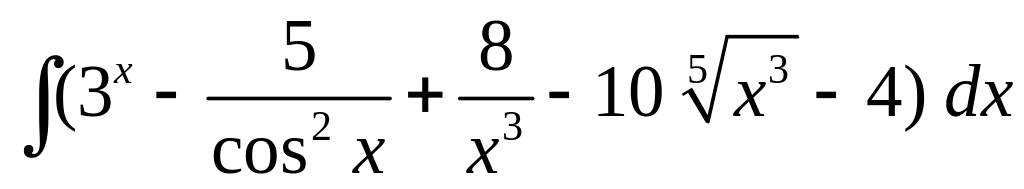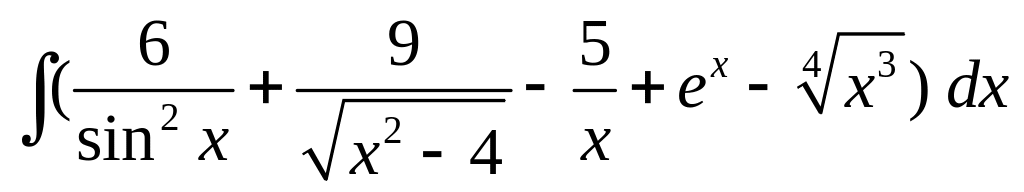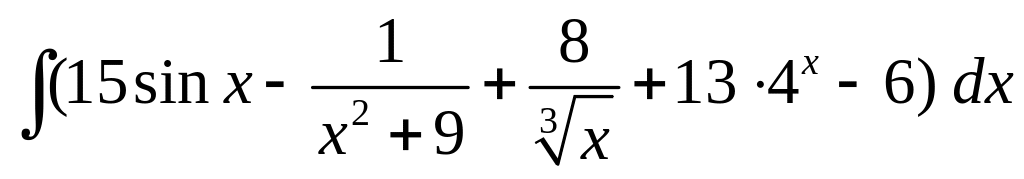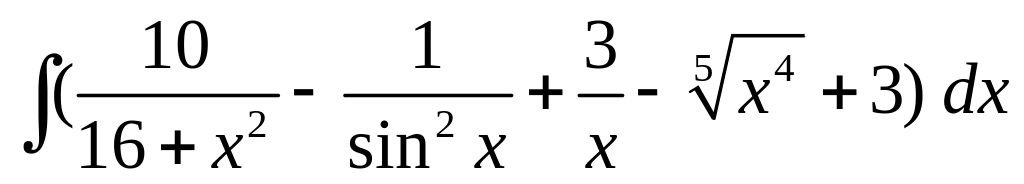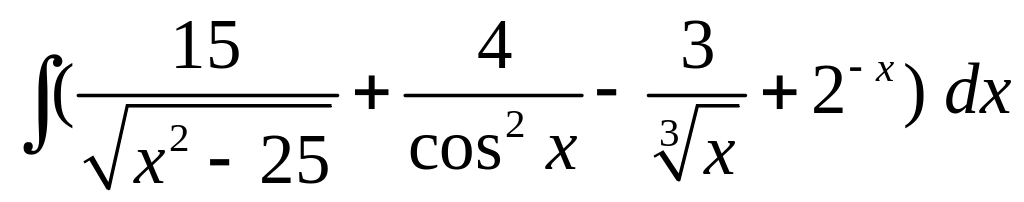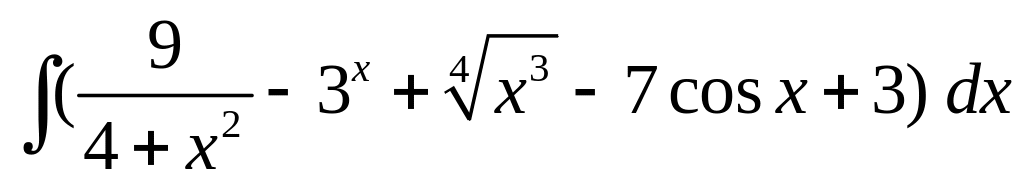
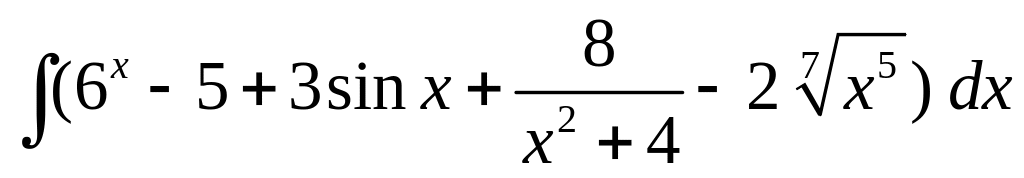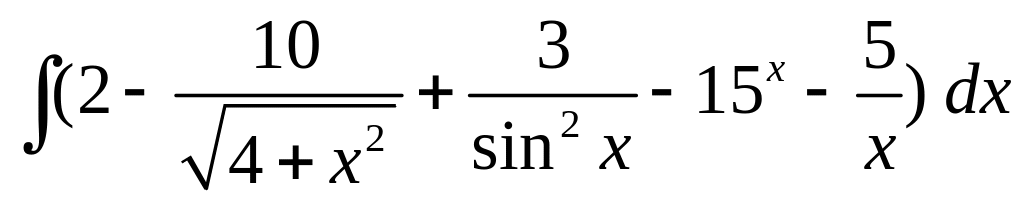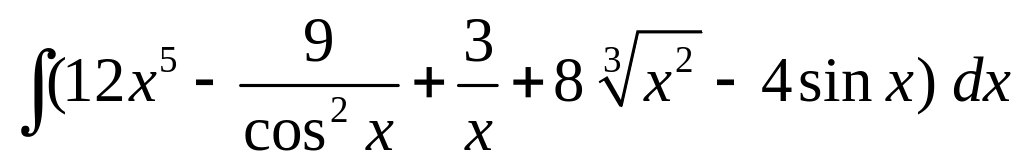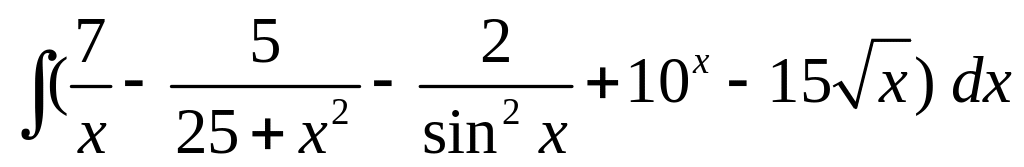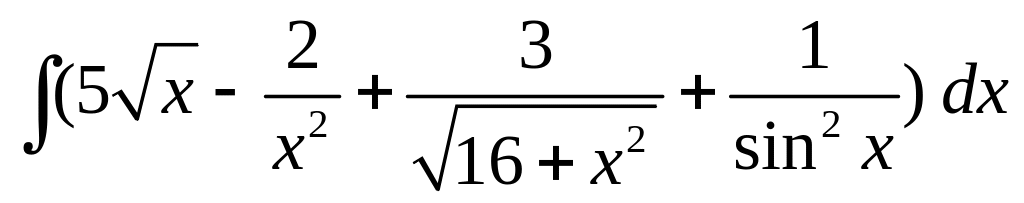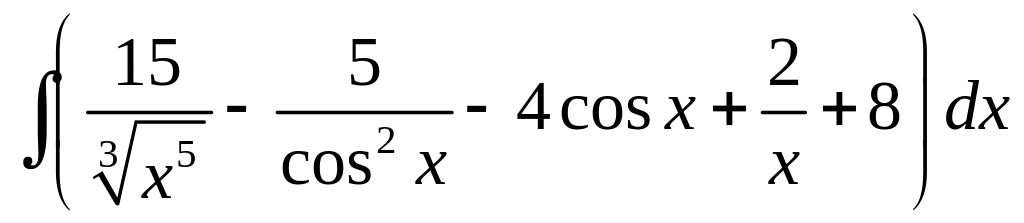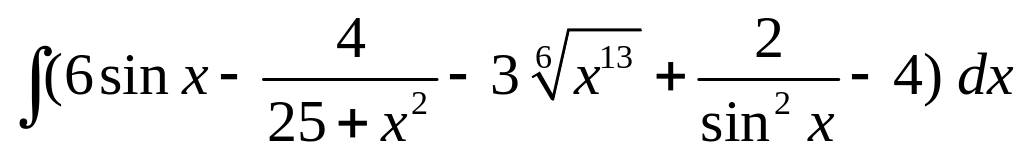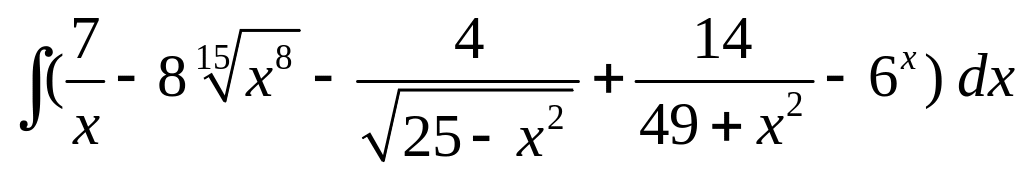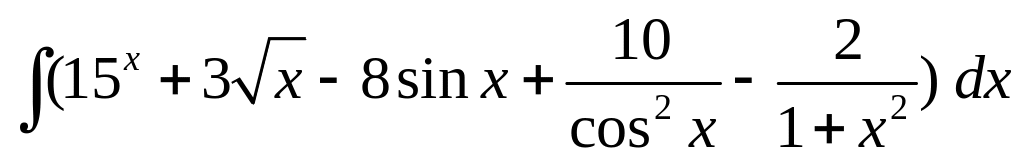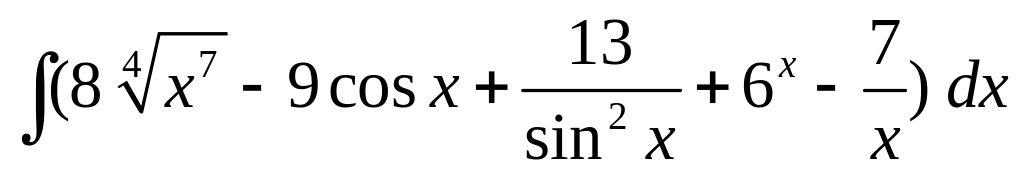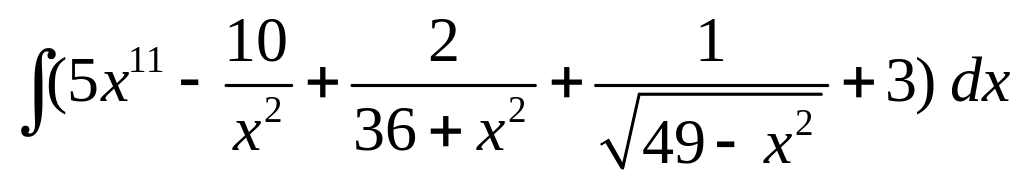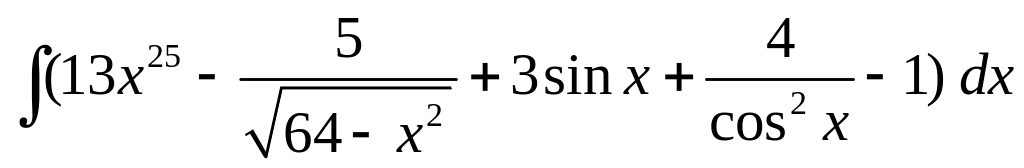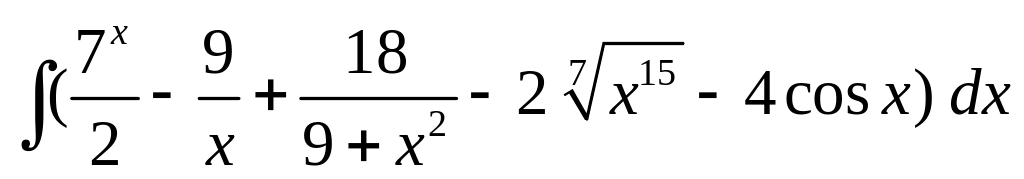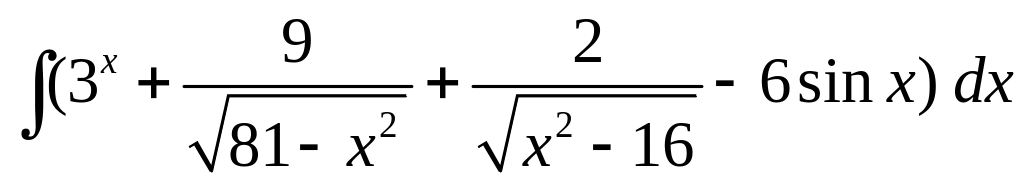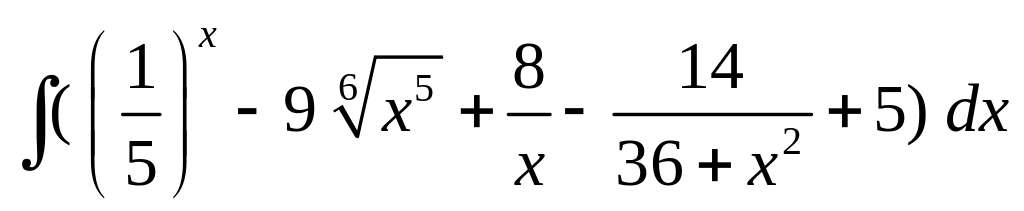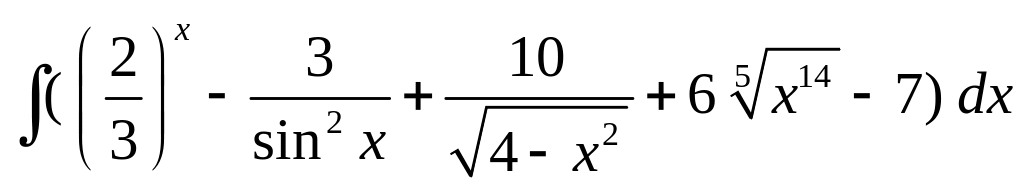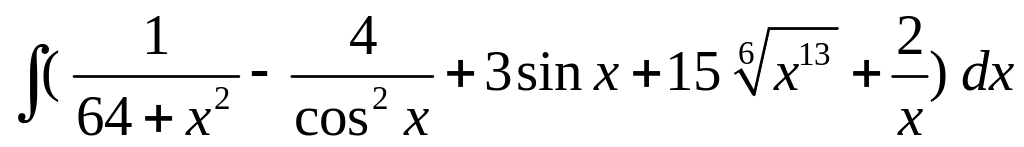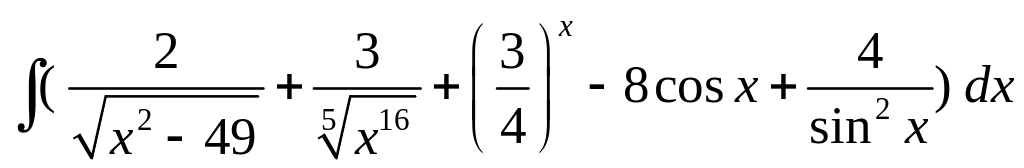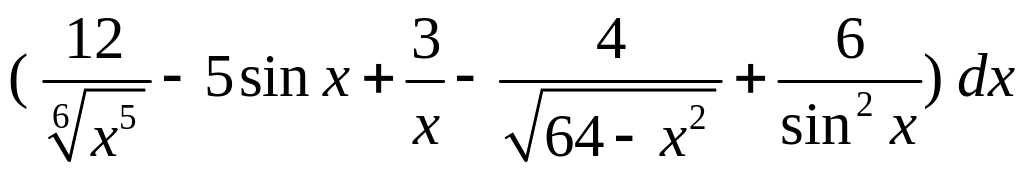Задание 2

Найдите интегралы.

1. а) ; б) ; в) ;

2. а) ; б) ; в) ;

3. а) ; б) ; в) ;

4. а) ; б) ; в) ;

5. а) ; б) ; в) ;

6. а) ; б) ; в) ;

7. а) ; б) ; в) ;

8. а) ; б) ; в) ;

9. а) ; б) ; в) ;

10. а) ; б) ; в) ;

11. а) ; б) ; в) ;

12. а) ;б) ; в) ;

13. а) ; б) ; в) ;

14. а) ; б) ; в) ;

15. а) ; б) ; в) ;

16. а) ; б) ; в) ;

17. а) ; б) ; в) ;

18. а) ; б) ; в) ;

19. а) ; б) ; в) ;

20. а) ; б) ;в) ;

21. а) ; б) ; в) ;

22. а) ;б) ; в) ;

23. а) ; б) ; в) ;

24. а) ; б) ; в) ;

25. а) ; б) ; в) ;

26. а) ; б) ; в) ;

27. а) ; б) ;в) ;

28. а) ; б) ; в) ;

29. а) ; б) ; в) ;

30. а) ; б) ; в) .