
- •I. Неопределенный интеграл
- •1. Таблица основных неопределённых интегралов
- •2. Основные свойства неопределённого интеграла
- •3. Замена переменной в неопределенном интеграле
- •Решение.
- •4. Интегрирование по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •II. Определенный интеграл
- •1. Формула Ньютона-Лейбница
- •III. Несобственные интегралы
- •1. Несобственный интеграл I рода.
- •2. Несобственный интеграл II рода.
- •IV. Геометрические приложения определенного интеграла
- •1. Вычисление площадей плоских фигур
- •2. Вычисление длины дуги
- •3. Вычисление объёмов тел
- •Задание 1.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6.
- •Задание 7.
- •Задание 8.
- •Задание 9.
- •Задание 10
- •Задание 11.
- •Задание 12.
- •Задание 13.
- •Задание 14.
- •Задание 15.
- •Задание 16.
- •Задание 17.
- •Задание 18.
- •394026 Воронеж, Московский просп., 14
2. Несобственный интеграл II рода.
Пусть
функция f(x)
определена на [a; b)
и
![]() (или = – ).
Несобственный интеграл второго рода
функции f(x)
на [a; b
определяется равенством
(или = – ).
Несобственный интеграл второго рода
функции f(x)
на [a; b
определяется равенством
![]() .
.
Если
существует конечный предел в этом
равенстве, то говорят, что интеграл
![]() сходится, в противном случае – расходится.
сходится, в противном случае – расходится.
Аналогично
определяется несобственный интеграл
II рода для случаев
![]() и
и
![]() .
Если же f(x)
неограниченна в любой окрестности
некоторой внутренней точки
.
Если же f(x)
неограниченна в любой окрестности
некоторой внутренней точки
![]() ,
то полагают
,
то полагают
 .
.
Пример 26. Вычислить интегралы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение. а) Рассматривается несобственный интеграл 2-го рода, так как подынтегральная функция терпит разрыв на правом конце промежутка интегрирования. На основании определения
![]() если этот предел
конечен. Имеем:
если этот предел
конечен. Имеем:

б)
![]()

![]() .
.
в)
![]()
![]() ,
,
значит, интеграл расходится.
Формулировки признаков сходимости для несобственных интегралов II рода по существу ничем не отличаются от формулировок признаков сходимости для несобственных интегралов I рода. Для применения этих признаков полезно пользоваться тем, что
![]() ,
,
![]()
![]()
Пример 27. Исследовать на сходимость интегралы:
а)
![]() ;
б)
;
б)
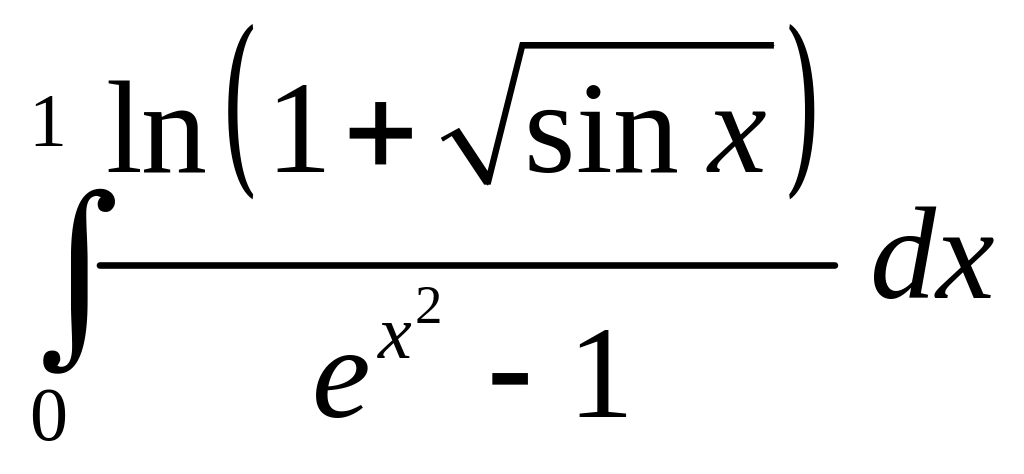 ; в)
; в)
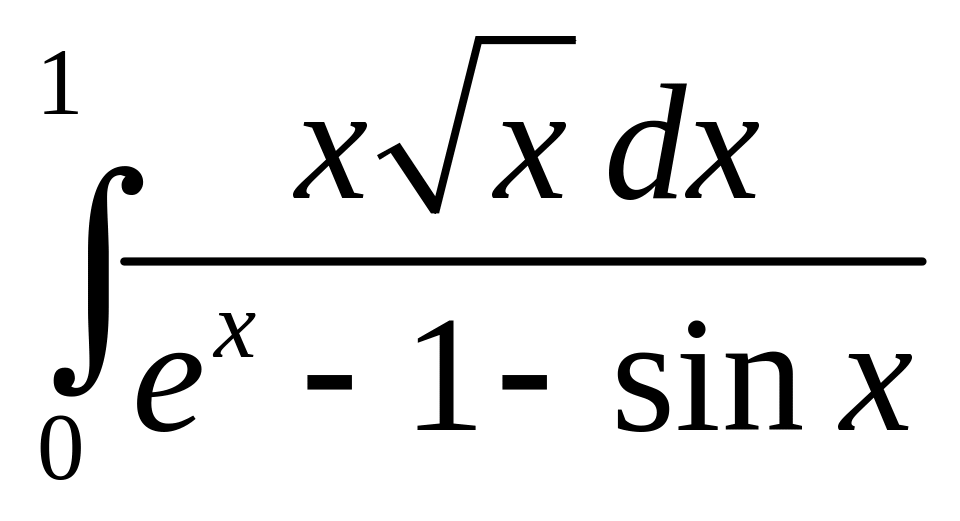 .
.
Решение.
а)
![]() .
Подынтегральная функция
.
Подынтегральная функция
![]() в промежутке [2; 3] имеет особую точку x
= 2. Множитель
в промежутке [2; 3] имеет особую точку x
= 2. Множитель
![]() стремится к 1/2 при
стремится к 1/2 при
![]() .
Поэтому естественно ожидать, что наша
функция в окрестности точки x
= 2 ведёт себя как
.
Поэтому естественно ожидать, что наша
функция в окрестности точки x
= 2 ведёт себя как
![]() ;
проверим это:
;
проверим это:
![]() .
.
Следовательно,
согласно второму признаку сходимости,
интегралы
![]() и
и
![]() ведут себя одинаково в смысле сходимости.
Но второй интеграл сходится (p
= 1/2 < 1), поэтому сходится и наш
интеграл.
ведут себя одинаково в смысле сходимости.
Но второй интеграл сходится (p
= 1/2 < 1), поэтому сходится и наш
интеграл.
б)
Функция
![]() имеет на промежутке [0; 1] одну особую
точку x = 0. Функции
имеет на промежутке [0; 1] одну особую
точку x = 0. Функции
![]() и
и
![]() являются бесконечно малыми величинами
при
являются бесконечно малыми величинами
при
![]() .
Известно, что
.
Известно, что
![]()
![]() ,
x2 при
.
Поэтому
,
x2 при
.
Поэтому
![]()
![]() при
при
![]() .
А так как
.
А так как
![]() расходится (p = 3/2 > 1 ), то
расходится и наш интеграл.
расходится (p = 3/2 > 1 ), то
расходится и наш интеграл.
в)
Разложим знаменатель (
![]() ) подынтегральной функции
) подынтегральной функции
![]() по формуле Тейлора в окрестности особой
точки
по формуле Тейлора в окрестности особой
точки
![]() функции
функции
.
![]()
![]() .
.
Следовательно,
![]()
![]()
![]() .
.
Известно,
что
![]() сходится, следовательно, сходится и
наш интеграл.
сходится, следовательно, сходится и
наш интеграл.
IV. Геометрические приложения определенного интеграла
1. Вычисление площадей плоских фигур
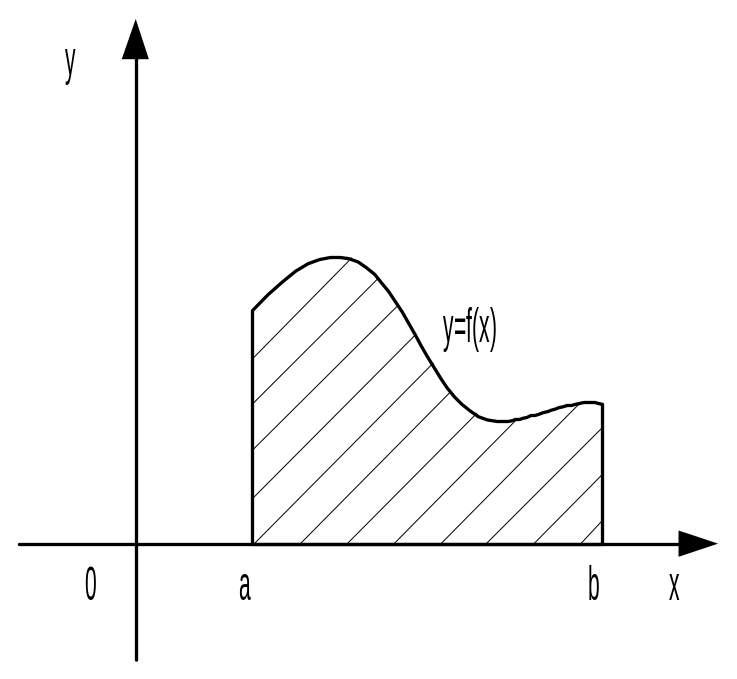
Площадь
криволинейной трапеции, ограниченной
графиками функций x
= a, x
= b, y
= 0, y = f(x)
( f(x)
0 при
x
[a; b]),
находится по формуле
![]() .
.
Рис.1.
Если фигура (D)
ограничена графиками функций x
= a, x
= b, y
= f(x),
y = g(x),
f(x)
g(x),
при x
[a; b],
то площадь S фигуры (D)
находится по формуле
![]() .
.
Рис.2.
Для определения площадей фигур, ограниченных сверху и снизу заданными кривыми f(x) и g(x), прежде чем применять формулу для нахождения площади часто бывает необходимо определить пределы интегрирования, т.е. абсциссы точек пересечения кривых f(x) и g(x). Они находятся как решения уравнения f(x) = g(x). Если корни этого уравнения (в порядке возрастания) х1 и х2, то х1 – нижний предел интегрирования, а х2 – верхний предел.
Пример 28. Найти площадь S фигуры (D), ограниченной линиями y = –x2 + 2x + 2 и y = 2x + 1.
Решение. Найдём абсциссы точек пересечения графиков функций, для чего решим уравнение: –x2 + 2x + 2 = 2x + 1; x2 – 1 = 0; x1 = –1, x2 = 1. Для всех точек x из отрезка [-1; 1] –x2 + 2x + 2 2x + 1. Поэтому
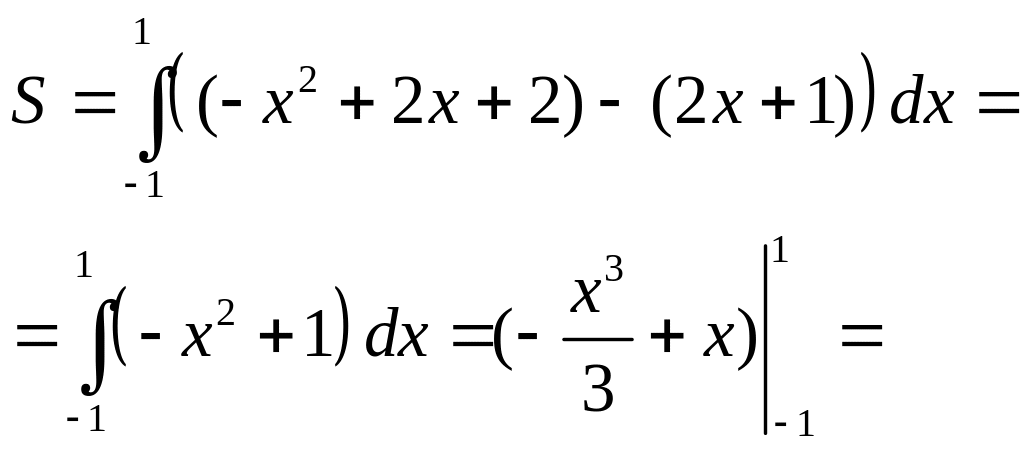
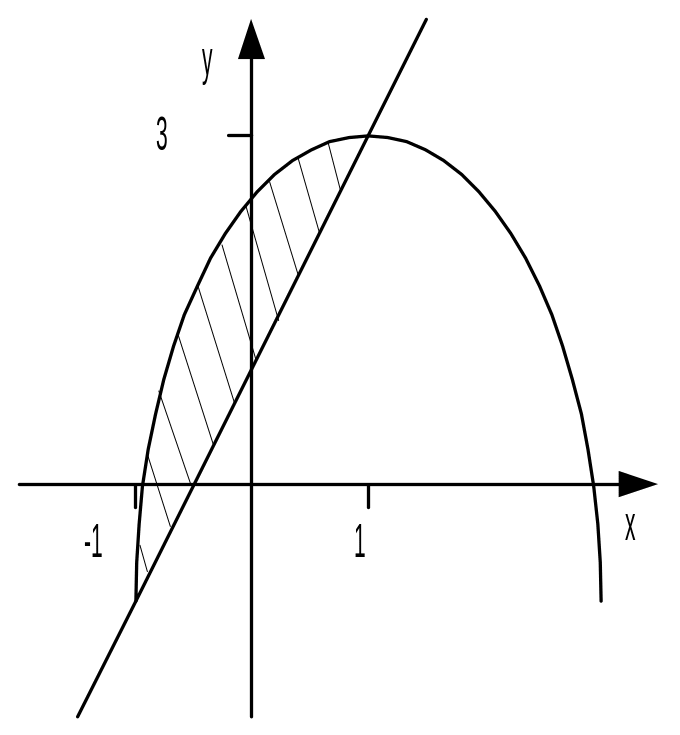
![]() .
.
Рис.3.
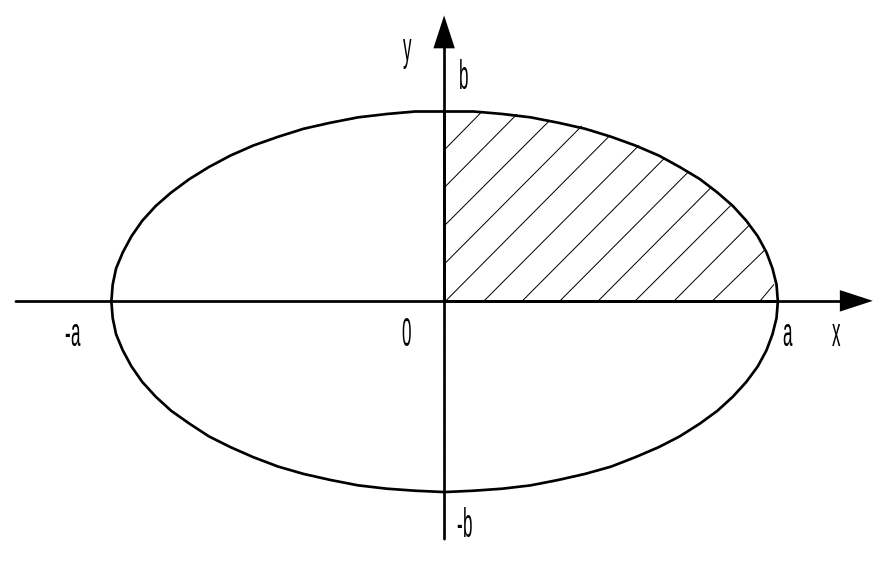 Пример 29.
Найти площадь фигуры, ограниченной
эллипсом
Пример 29.
Найти площадь фигуры, ограниченной
эллипсом
![]() .
.
Рис.4.
Решение.
Эллипс имеет две оси симметрии:
координатные оси 0х и 0у. Поэтому площадь
S фигуры равна
учетверённой площади S1
части (D1) фигуры,
расположенной в первой четверти
(заштриховано). Фигура (D1)
ограничена сверху линией
![]() , снизу – осью 0х, слева – осью 0у.
Поэтому
, снизу – осью 0х, слева – осью 0у.
Поэтому


Отсюда находим S = 4S1 = ab.
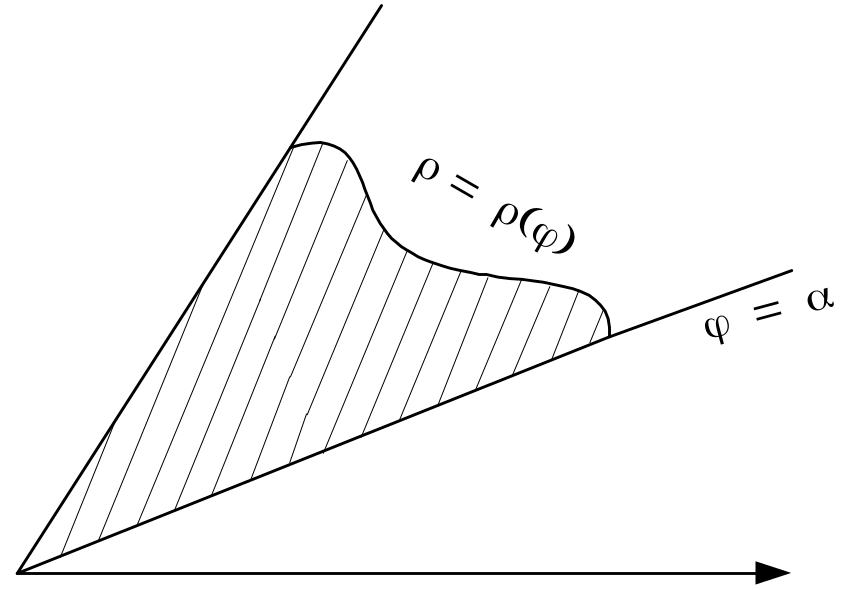 Площадь S
криволинейного сектора, ограниченного
графиком функции
Площадь S
криволинейного сектора, ограниченного
графиком функции
![]() и лучами
и лучами
![]() и
и
![]() в полярной системе координат, находится
по формуле
в полярной системе координат, находится
по формуле
 .
.
Рис.5.
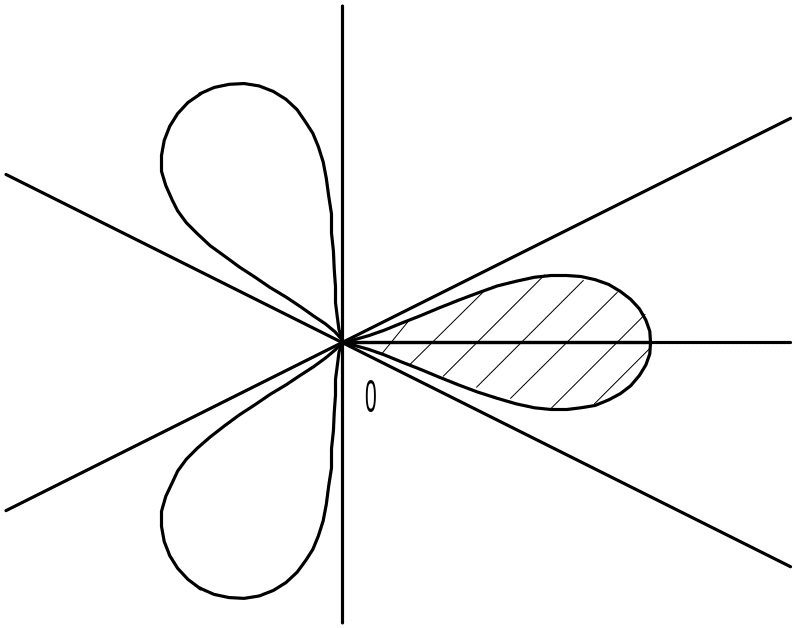
Пример
30. Найти площадь S
фигуры, ограниченной линией, заданной
в полярной системе координат уравнением
![]() .
.
Решение.
Начнём с изображения линии. Так как
![]() ,
то нам нужно сначала решить неравенство
,
то нам нужно сначала решить неравенство
![]() .
Имеем
.
Имеем
![]() ,
,
![]()
![]()
 ,
,
![]() .
.
При
n = 0:
![]() ;
;
при
n = 1:
![]() ;
;
при
n = 2:
![]() ;
Рис. 6.
;
Рис. 6.
при
n = 3:
![]() – этот угол является повторением угла,
соответствующего значению n
= 0. Рассмотрение других значений приводит
к уже полученным углам на плоскости.
Рассмотрим рисунок. Наша фигура ограничена
тремя лепестками. Её площадь S
равна 3S1, где S1
– площадь одного лепестка (заштриховано).
– этот угол является повторением угла,
соответствующего значению n
= 0. Рассмотрение других значений приводит
к уже полученным углам на плоскости.
Рассмотрим рисунок. Наша фигура ограничена
тремя лепестками. Её площадь S
равна 3S1, где S1
– площадь одного лепестка (заштриховано).
Имеем
![]()
 .
.
Отсюда находим S = 3S1, = .
