
- •I. Неопределенный интеграл
- •1. Таблица основных неопределённых интегралов
- •2. Основные свойства неопределённого интеграла
- •3. Замена переменной в неопределенном интеграле
- •Решение.
- •4. Интегрирование по частям
- •5. Интегрирование рациональных дробей
- •6. Интегрирование иррациональных выражений
- •7. Интегрирование тригонометрических функций
- •II. Определенный интеграл
- •1. Формула Ньютона-Лейбница
- •III. Несобственные интегралы
- •1. Несобственный интеграл I рода.
- •2. Несобственный интеграл II рода.
- •IV. Геометрические приложения определенного интеграла
- •1. Вычисление площадей плоских фигур
- •2. Вычисление длины дуги
- •3. Вычисление объёмов тел
- •Задание 1.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6.
- •Задание 7.
- •Задание 8.
- •Задание 9.
- •Задание 10
- •Задание 11.
- •Задание 12.
- •Задание 13.
- •Задание 14.
- •Задание 15.
- •Задание 16.
- •Задание 17.
- •Задание 18.
- •394026 Воронеж, Московский просп., 14
7. Интегрирование тригонометрических функций
В зависимости от вида подынтегральной функции можно применять для упрощения тригонометрического выражения различные способы.
Для
интегралов вида
![]() :
:
а) если хотя бы одно из чисел т,п – нечетное (например, m = 2k + 1), то
![]() .
.
Пример 14.
![]()
б) если т и п – четные, положительные, то степени понижаются сведением к двойному углу по формулам
![]()
Пример 15.
![]()
![]()
![]() в) Если т,п
– четные и хотя бы одно из них отрицательно
(или если т
и п
– отрицательные числа одинаковой
четности), то используем соотношения
в) Если т,п
– четные и хотя бы одно из них отрицательно
(или если т
и п
– отрицательные числа одинаковой
четности), то используем соотношения
![]()
Пример
16.
![]()
![]()
Пример
17.
![]()
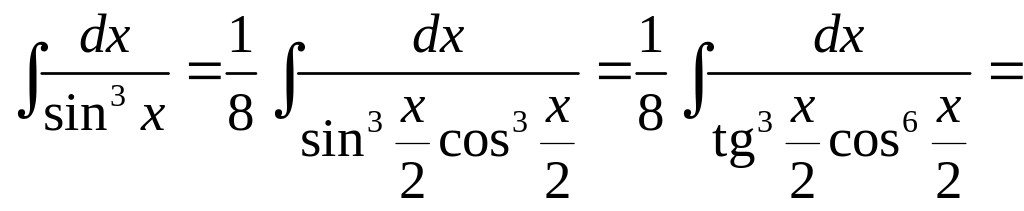
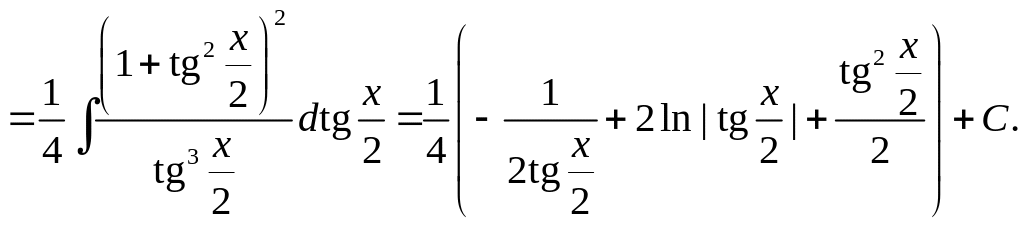
Интегралы вида
![]()
приводятся к табличным с помощью формул
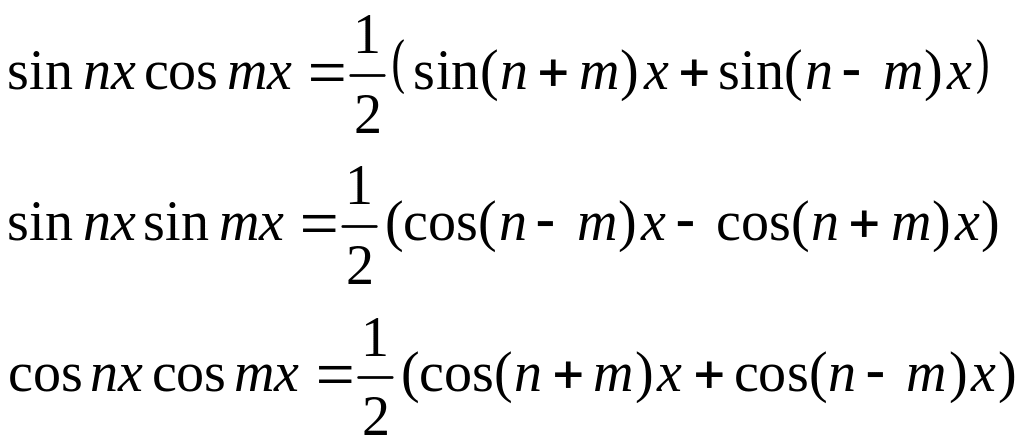
Пример
18.
![]()
![]() Интегралы вида
Интегралы вида
![]() ,
где R
– рациональная функция, приводятся к
интегралам от рациональных функций
новой переменной t
в общем случае с помощью подстановки
,
где R
– рациональная функция, приводятся к
интегралам от рациональных функций
новой переменной t
в общем случае с помощью подстановки
![]() ,
откуда
,
откуда
![]() .
В случае четности R
по sin
x
и cos
x:
R(-sin
x,
-cos
x)
= R(sin
x,
cos
x)
используем подстановку t
= tg
x,
откуда
.
В случае четности R
по sin
x
и cos
x:
R(-sin
x,
-cos
x)
= R(sin
x,
cos
x)
используем подстановку t
= tg
x,
откуда
![]() .
.
Пример
19.
![]() .
.
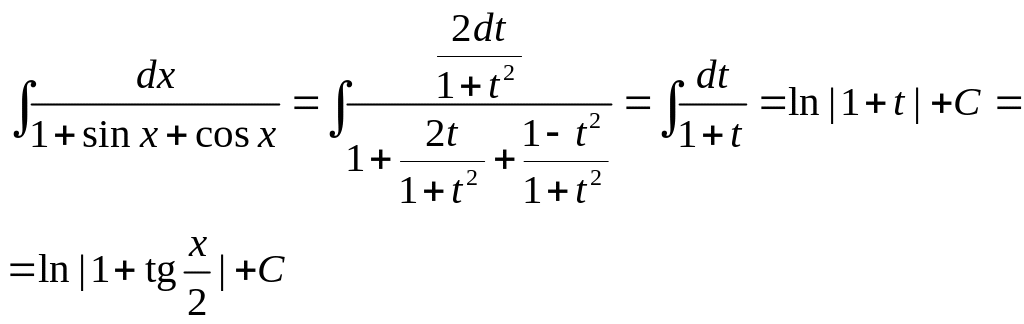
При вычислении интеграла применена подстановка .
Пример
20.
![]()
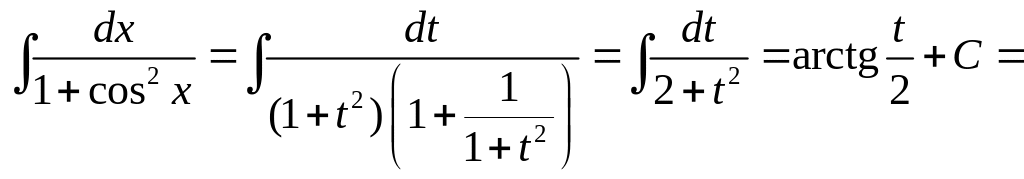
![]()
Здесь использовалась замена t = tg x .
II. Определенный интеграл
1. Формула Ньютона-Лейбница
Для вычисления определенных интегралов от непрерывных функций с конечными пределами необходимо, пользуясь известными методами интегрирования, получить первообразную от интегрируемой функции и, применяя формулу Ньютона-Лейбница
![]()
найти разность значений первообразной при подстановке вместо переменной верхнего и нижнего пределов интегрирования.
Пример
21. Найти
![]() .
.
Решение.
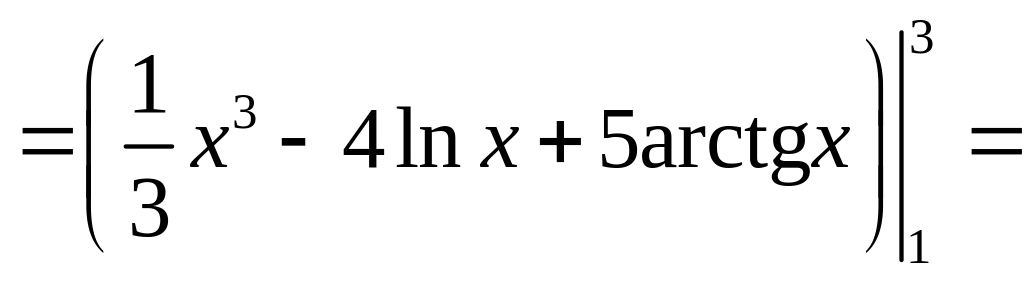
![]()
![]() .
.
Пример
22. Вычислить интеграл
![]() .
.
Решение. Воспользуемся формулой замены переменной в определенном интеграле:

и
применим подстановку
![]() т.е. x
= t².
Определим новый промежуток интегрирования:
х
= 4 при t
= 2; х
= 9 при t
= 3. Следовательно,
т.е. x
= t².
Определим новый промежуток интегрирования:
х
= 4 при t
= 2; х
= 9 при t
= 3. Следовательно,
![]() Пример 23.
Вычислить
Пример 23.
Вычислить
![]() .
.
Решение.
Воспользуемся формулой интегрирования
по частям в определенном интеграле
![]()
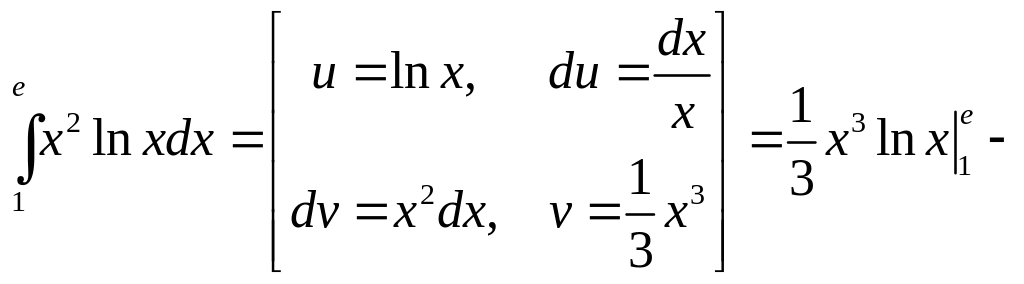
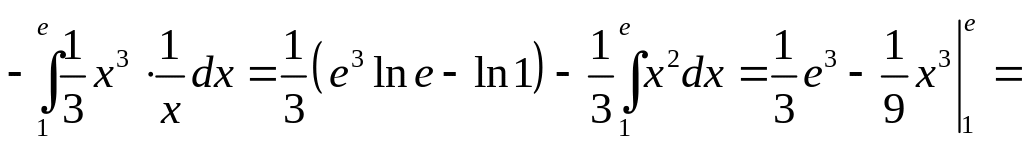
![]() .
.
III. Несобственные интегралы
1. Несобственный интеграл I рода.
Пусть
функция f(x)
определена на
![]() и интегрируема на отрезке [a;
b] для любого b
> a. Несобственный
интеграл первого рода определяется
равенством
и интегрируема на отрезке [a;
b] для любого b
> a. Несобственный
интеграл первого рода определяется
равенством
![]() .
.
Если существует конечный предел в этом равенстве, то интеграл называется сходящимся, в противном случае – расходящимся.
Аналогично
определяются несобственные интегралы
![]() и
и
![]() :
:![]() ,
,
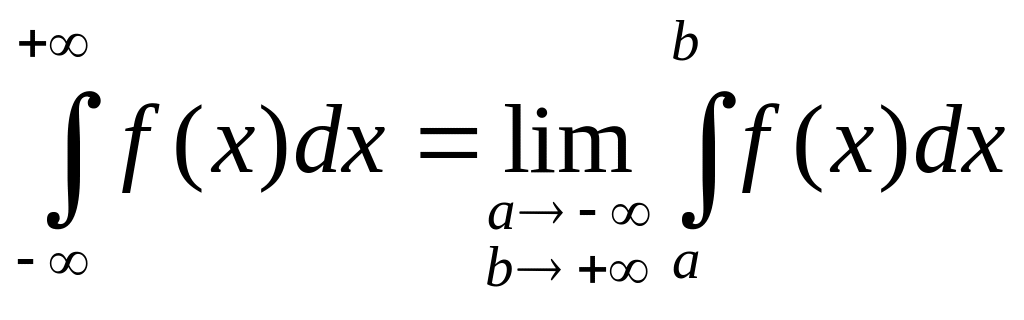 .
.
Пример 24. Вычислить
а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение.
а)
![]()
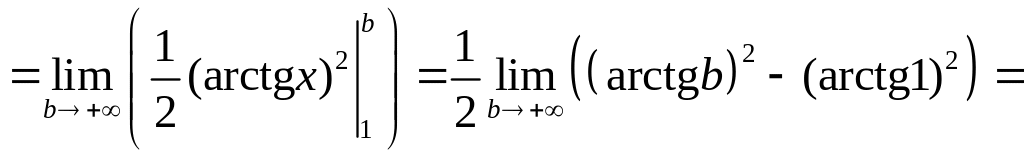
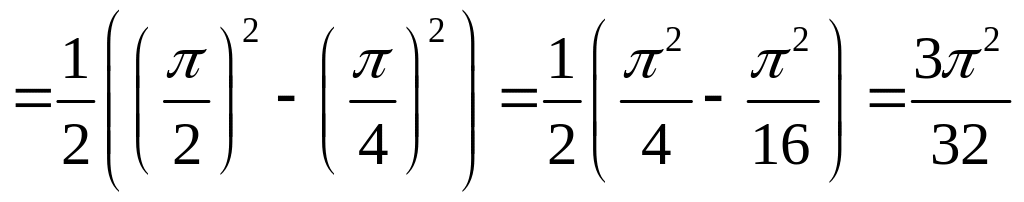 .
.
б)
![]()
![]() ,
,
и интеграл расходится;
в)
![]()
![]() .
.
Для исследования вопроса сходимости несобственного интеграла часто оказывается полезным следующий факт (a > 0):
![]()
Аналогичное
утверждение справедливо для интеграла
![]() ,
,
b
< 0, и![]() ,
a > c.
,
a > c.
Теорема
(первый признак сходимости). Пусть
f(x)
и g(x)
определены на
,
для любого b>a
f(x),
g(x)
интегрируемы на
![]() и
и
![]()
![]() .
Тогда
.
Тогда
если
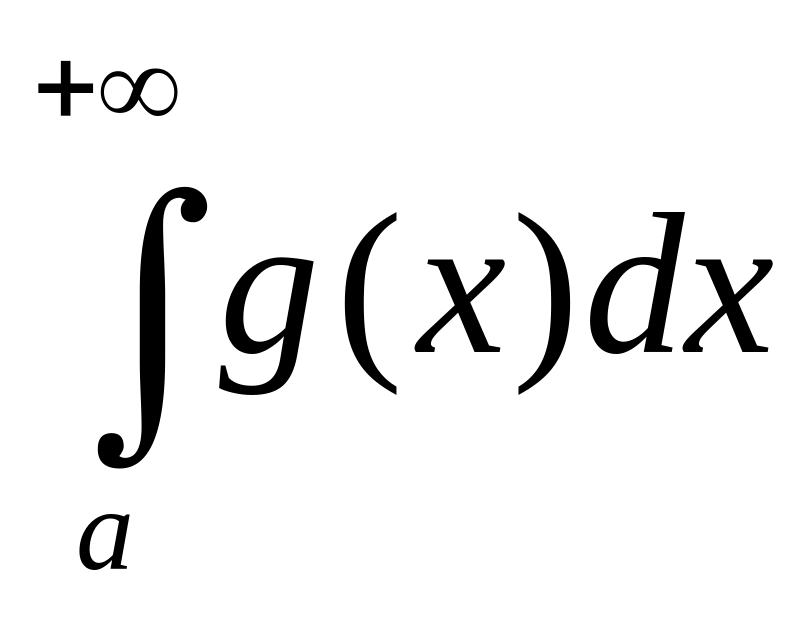 сходится, то сходится и
сходится, то сходится и
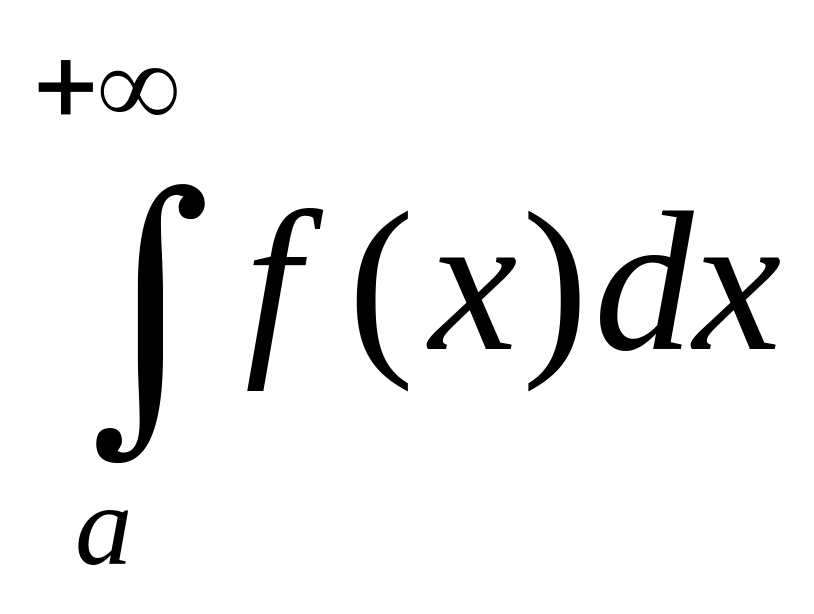 ;
;если расходится, то расходится и .
Теорема
(второй признак сходимости). Пусть
f(x)
и g(x)
определены на
,
![]() и пусть существует конечный предел
и пусть существует конечный предел
![]() .
Тогда интегралы
,
ведут себя одинаково в смысле сходимости
(т.е. одновременно сходятся или расходятся).
.
Тогда интегралы
,
ведут себя одинаково в смысле сходимости
(т.е. одновременно сходятся или расходятся).
Теорема.
Если
![]() сходится, то сходится и
(в таком случае говорят, что
сходится абсолютно).
сходится, то сходится и
(в таком случае говорят, что
сходится абсолютно).
Аналогичные утверждения справедливы для несобственного интеграла .
Пример 25. Исследовать на сходимость интегралы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение.
а) Применим
теорему сравнения. В нашем случае при
х ≥ 1
справедливо неравенство
![]() .
Рассмотрим
.
Рассмотрим
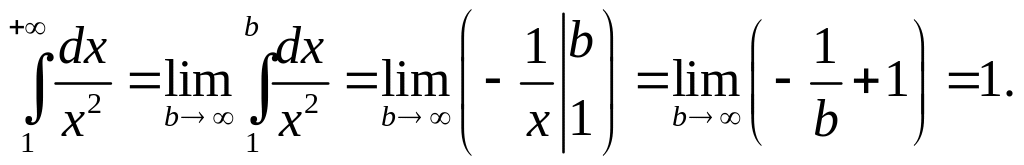 Так как
Так как
![]() сходится, то на основании теоремы
сравнения несобственный интеграл
сходится.
сходится, то на основании теоремы
сравнения несобственный интеграл
сходится.
б)
![]() является иррациональной функцией;
степень числителя равна 3/2 (числитель
можно представить как
является иррациональной функцией;
степень числителя равна 3/2 (числитель
можно представить как
![]() ),
степень знаменателя равна 2. Рассмотрим
вспомогательную функцию
),
степень знаменателя равна 2. Рассмотрим
вспомогательную функцию
![]() .
Докажем, что существует конечный предел
.
Докажем, что существует конечный предел
![]() ,
не равный 0. Действительно,
,
не равный 0. Действительно,
![]()
![]() .
Поэтому
.
Поэтому
![]() ,
,
![]() ведут себя одинаково в смысле сходимости.
А так как
ведут себя одинаково в смысле сходимости.
А так как
![]() расходится, то расходится и
.
расходится, то расходится и
.
в)
Обозначим
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Интеграл
.
Интеграл
![]() сходится (доказывается это как и выше:
сходится (доказывается это как и выше:
![]() ,
,
![]() сходится и можно воспользоваться вторым
признаком сходимости).
сходится и можно воспользоваться вторым
признаком сходимости).
