Ответы и указания

1. Экстремалями являются окружности .

2. Интервал не зависит от пути интегрирования. Вариационная задача лишена смысла.

3. В классе непрерывных функций экстремум не достигается.

4. Экстремалями являются гиперболы .

_5. .

_6. .

_7. .

_8. .

_9. .

_10. .

_11. , , откуда z легко находится.

12. .

_13. .

_14. .

_15. .

_16. .

_17. .

_18.

3. Условные экстремумы

3.1 Условный экстремум с интегральными связями

Вернёмся к функционалу и предположим, что функция y(x) берется не произвольной, а должна помимо граничных условий , удовлетворят дополнительному условию вида

(20)

(g-заданное число).

Тогда и вариация должна удовлетворять дополнительному условию, полученному линеаризацией (20):

.

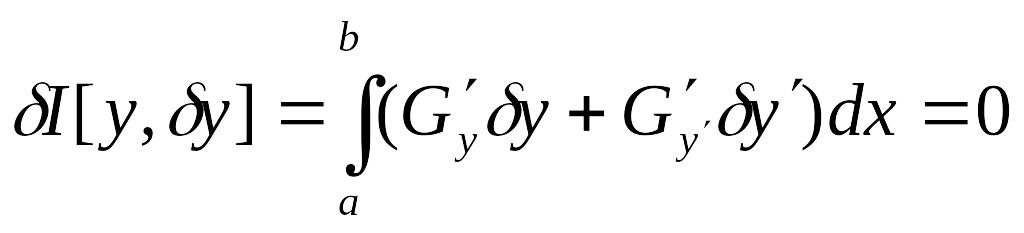Пусть функция реализует экстремум рассматриваемого функционала при заданных граничных условиях и связи (20). Тогда можно поступить следующим образом. Разобьём отрезок [a, b] на большое число равных частей длины , обозначим . Заменим интеграл интегральной суммой, а производную на разделённую разность. Приходим к следующей задаче на условный экстремум: найти экстремум величины

при заданных значениях и при условии

.

Таким образом, мы приходим к задаче на уловный экстремум с функциями конечного числа переменных . Согласно теории такого экстремума, следует написать условия безусловного экстремума для функции .

Возвращаясь к интегралам, получаем, что для отыскания функции , реализующей условный экстремум, следует написать уравнение Эйлера для функции

(21)

Общее решение этого уравнения содержит две произвольные постоянные и параметр , которые находятся из двух граничных условий и уравнения связи (20). Параметр (множитель Лагранжа), как показано в математическом анализе, равен .

Если имеется несколько условий вида (20)

,

то вместо (21) надо воспользоваться функцией

.

Пример11. Максимизировать функционал при граничных условиях и условии .

Решение. Согласно сказанному выше, нужно решить уравнение Эйлера для функции . Т.к. в неё не входит явно х, то можно воспользоваться первым интегралом (16’) . Имеем

Найдём из этого уравнения :

Отсюда

Разделяем переменные и интегрируем:

Получаем уравнение окружностей. Постоянные и определяются из граничных условий и заданной связью, т.е. из всех дуг окружностей надо выбрать ту, которая имеет заданную длину L.

Вариационные задачи с интегральными связями широко распространены. В ряде случаев требуется распорядиться определёнными ресурсами, чтобы получить максимальную выгоду. Если при этом возможная линия определяется произвольной функцией, то для её отыскания получается вариационная задача, в которой задание ресурсов, определяют интегральные связи.

3.2. Условный экстремум с конечными или дифференциальными связями

Для определённости рассмотрим функционал с тремя искомыми функциями .

(22)

Пусть на них наложена конечная (голономная) связь

, (23)

где h(x) – заданная функция. Тогда для вариаций этих функций имеем очевидное соотношение

.

Пусть надо решить задачу об экстремуме функционала (22) при конечной связи (23) и граничных условиях

,

удовлетворяющих уравнению связи, т.е.

. Это – условия согласования граничных условий со связью.

Далее можно рассуждать, как в п. 3.1, но тогда вместо (20’) появятся соотношения

(23’)

В сему правила отыскания условного экстремума надо для каждой левой части (23’) взять свой множитель Лагранжа, т.е. искать безусловный экстремум для функции

.

Возвращаемся к интегралам. Получается, что для отыскания функций , реализующих условный экстремум, следует написать систему уравнений для функции

с фиксированной (т.е. не варьируемой) но неизвестной заранее функций (функциональный множитель Лагранжа). Уравнения Эйлера вместе с уравнением связи (23) образуют систему из четырёх уравнений с четырьмя искомыми функциями . Произвольные постоянные, которые появятся при её интегрировании, определяются граничными условиями.

В качестве примера рассмотрим задачу С.А.Чаплыгина.

Пример12. Найти максимальную площадь, облетаемую самолётом за заданное время T при постоянном ветре.

Решение. Обозначим через v скорость ветра и выберем ось ОУ в направлении этой скорости (рис. 11). Через V обозначим скорость самолёта относительно воздуха. Тогда должно выполнятся соотношение

(а),

где точкой обозначена производная по времени.

Выражение для площади, ограниченной замкнутым контуром

имеет вид (в)

Получилась задача о максимизации интеграла (в) при дифференциальной связи (а). Согласно доказанному нужно составить систему уравнений Эйлера для функции .

Для этого воспользуемся уравнениями (19’), заменив в них

на x(t) , на y(t) и x на t :

.

Интегрируя по t, получаем первые интегралы:

или

Путём параллельного переноса осей координат всегда можно добиться чтобы : . Исключим r(t)

из этой системы, получим

Умножим обе части равенства на dt , получим

т.к. и

Подставим это значение dt в (а), получаем

Это – дифференциальное уравнение, связывающее только величины x и y. Оно является однородным относительно x и y.

Его можно решить подстановкой , но проще решить, переходя к полярным координатам . Подставляя в (с) , извлекая предварительно квадратный корень из обеих частей, получаем

.

Т.к. и , то

Обозначив , можно записать

Потенцируя, получаем По смыслу задачи . Поэтому данное уравнение определяет семейство Эллипсов с одинаковым эксцентриситетом , большая ось которых перпендикулярна направлению ветра.

Аналогичным образом рассматриваются дифференциальные (неголономные) связи вида .

Здесь также к функциям F надо добавить – r(x)H. Отличие будет в том, что в систему уравнений Эйлера теперь войдёт не только но . Задача на экстремум функционала с конечными или дифференциальными связями называется также задачей Лагранжа.

Задачи для самостоятельного решения

1. Найти экстремали изопериметрической задачи.

при условии ; y(0)=0; y(1)=0.

2. Найти геодезические линии круглого цилиндра r=R.

Указание: решение удобно искать в цилиндрических координатах r,,z.

3. Найти экстремали изопериметрической задачи при условии ( a=const)

4. Написать дифференциальное уравнение экстремалей изопериметрической задачи об экстремуме функционала

при условии ;y(0)=0;y(x1)=0.

. Ответы

1. где - целое .

2. ;

3. где определяются из граничных условий и из изопериметрического условия .

4. .

Тривиальное решение не удовлетворяет изопериметрическому условию . Нетривиальные решения существуют лишь при некоторых значениях называемых собственными значениями. Следовательно, должно быть собственным значением. Одна произвольная постоянная общего решения уравнения Эйлера определяется из условия , другая - из изопериметрического условия.