2.5.3. Простейшие случаи интегрируемости уравнения Эйлера

1. F не зависит от : .

Уравнение Эйлера имеет вид , т.к. . (12)

Решение (относительно ) этого конечного уравнения не содержит произвольных постоянных, поэтому, вообще говоря, не удовлетворяет граничным условиям , .

Следовательно, решение рассматриваемой вариационной задачи, вообще говоря, не существует. Лишь в исключительных случаях, когда кривая проходит через граничные точки и , существует кривая, на которой может достигаться экстремум.

2. зависит лишь от : .

Здесь и уравнение Эйлера имеет вид . Отсюда или .

Если , то . Если же уравнение один или несколько действительных корней , то . Это решение содержится в двухпараметрическом семействе . Таким образом, в этом случае экстремалями являются всевозможные прямые линии.

Пример 4. Длина дуги .

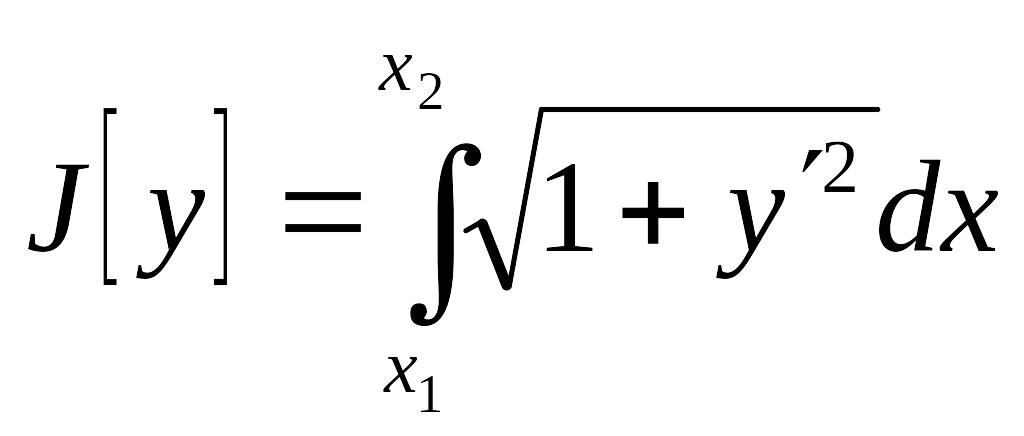Решение. Здесь тогда экстремали – прямые линии .

3. зависит лишь от и : . Из (15) следует, что уравнение Эйлера имеет вид

и, следовательно, имеет первый интеграл . Полученное уравнение первого порядка (относительно ) не содержит искомой функции.

Пример 5. Функционал 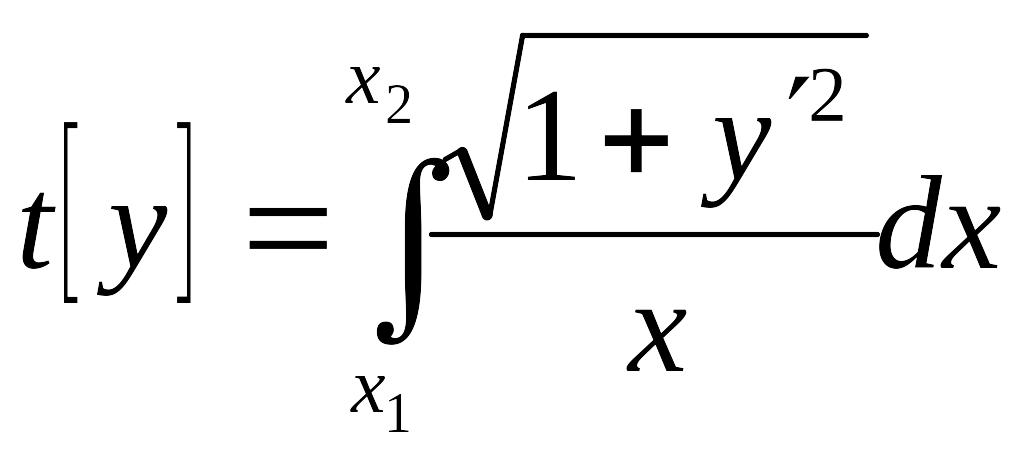определяет время, затрачиваемое на перемещение по кривой из одной точки в другую, если скорость движения . Действительно, из следует, что и .

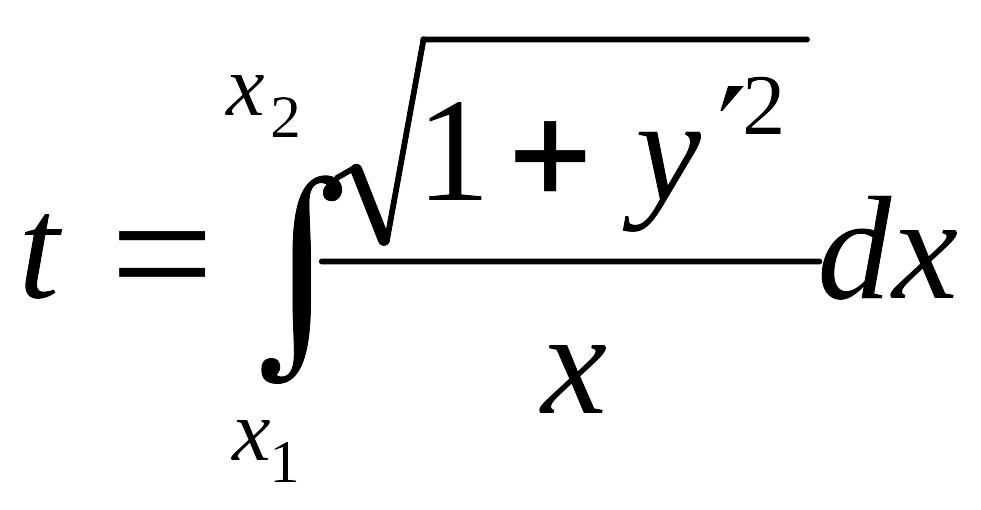Решение. Запишем первый интеграл уравнения Эйлера или .

Это уравнение проще всего решить, если ввести параметр, положив . Тогда

или , где .

;

. Таким образом,

; . Исключая , получим - семейство окружностей с центрами на оси ординат.

4. зависит лишь от и : . В этом случае в (16) отсутствует второе слагаемое

.

Умножим обе части этого уравнения на

.

Теперь это уравнение можно записать следующим образом:

.

Действительно,

.

Следовательно, уравнение Эйлера имеет первый интеграл

,

где - произвольная постоянная.

Пример 6. Определить кривую с заданными граничными точками, от вращения которой вокруг оси абсцисс образуется поверхность наименьшей площади (рис. 8).

Р ешение. Запишем выражение для площади поверхности вращения

.

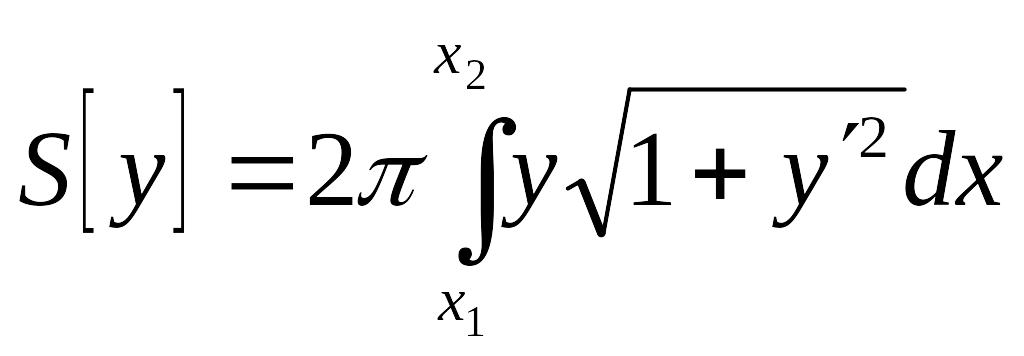Подынтегральная функция зависит только от и , следовательно, первый интеграл уравнений Эйлера имеет вид

.

В данном случае .

Приведем в левой части к общему знаменателю

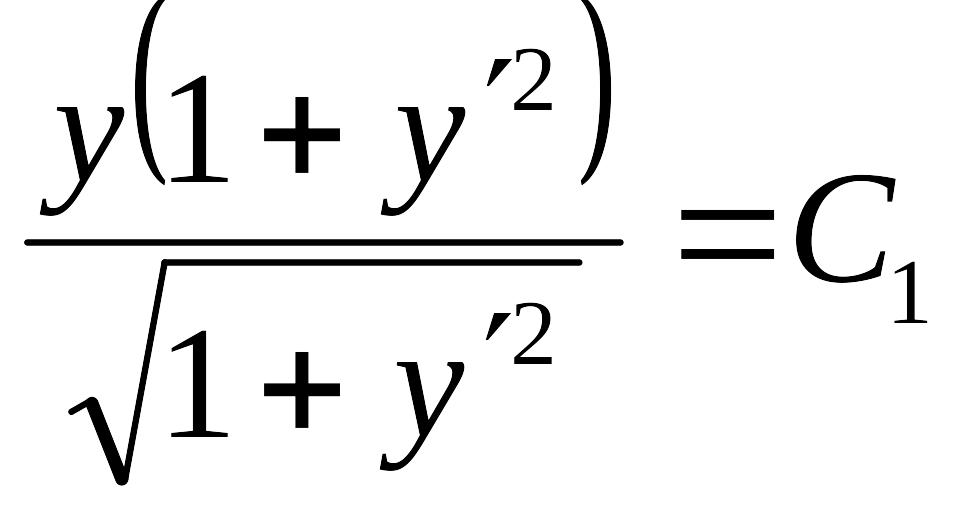или . Проще всего это уравнение интегрируется подстановкой , тогда из уравнения . Так как , то ; .

Следовательно, уравнение искомой линии в параметрической форме имеет вид

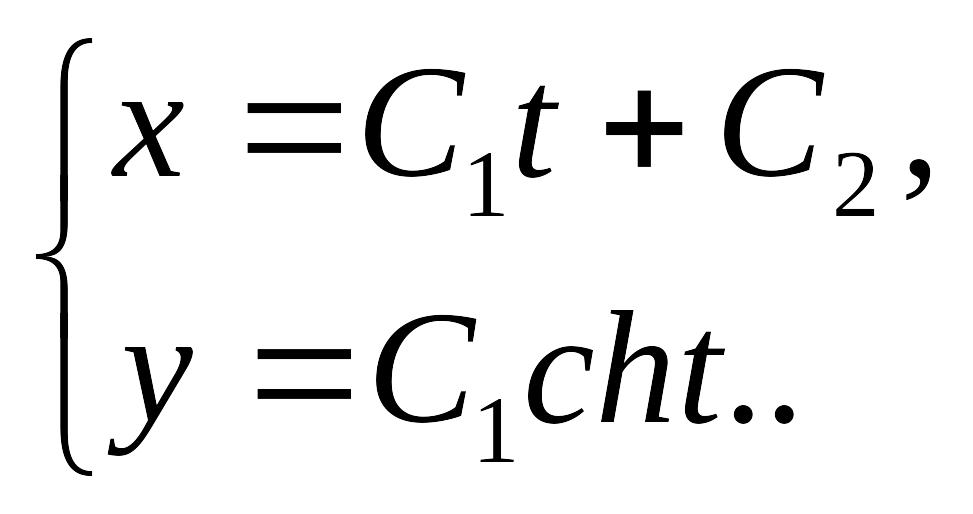
Исключая параметр , получим и . Это – семейство цепных линий, от вращения которых получаются поверхности, называемые катеноидами. Постоянные и определяются из условия прохождения искомой линии через заданные граничные точки. В зависимости от положения точек А и В может существовать одно, два или ни одного решения.

П ример 7. Определить кривую, соединяющую точки А и В, при движении по которой материальная точка скатывается из точки А в точку В в кратчайшее время (трением и сопротивлением среды пренебречь) (рис. 9).

Решение. Запишем закон сохранения энергии

, т.е. , откуда , , .

Следовательно, 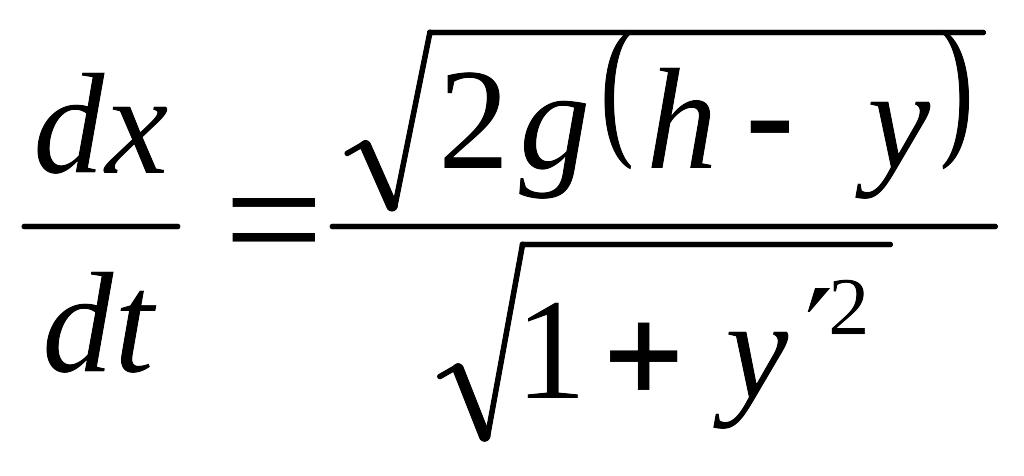, т.е. 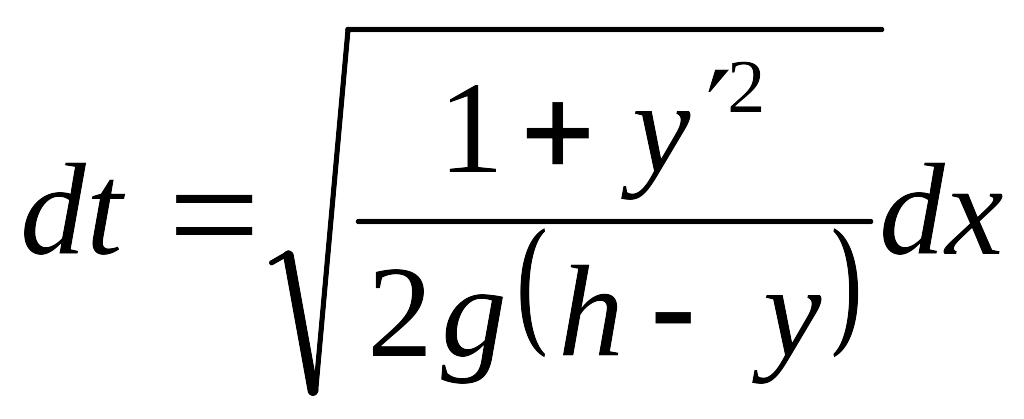. Поэтому .

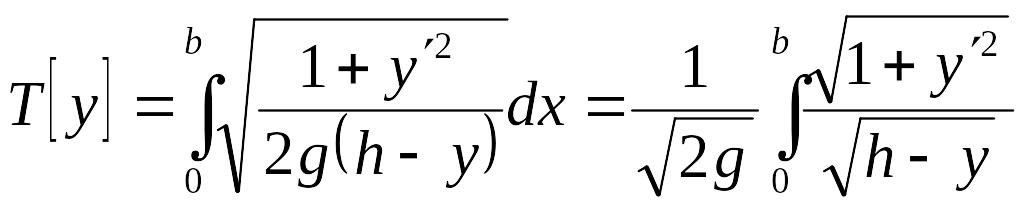Искомая функция должна удовлетворять граничным условиям , .

Полученный функционал не содержит явно , поэтому уравнение Эйлера имеет первый интеграл . В данном случае

.

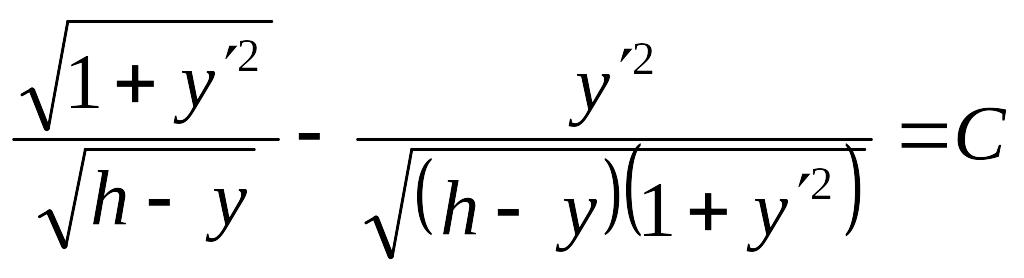Упростим левую часть.

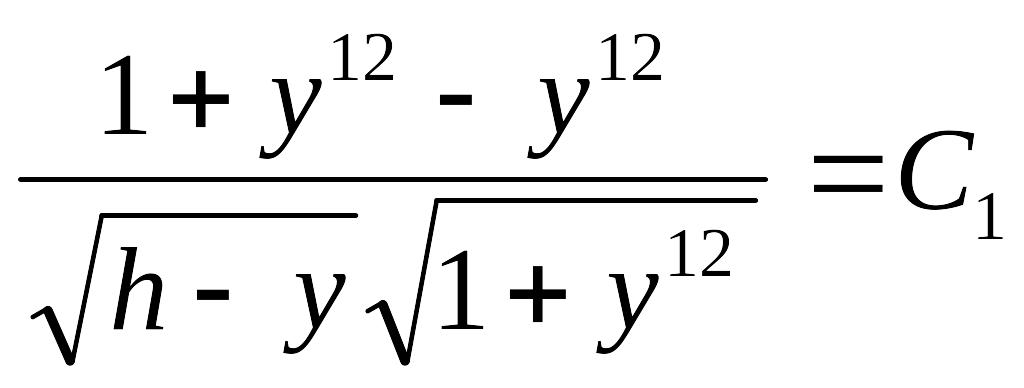или .

Полученное уравнение можно преобразовать к виду y’=f(y) и решить его. Однако лучше совершить искусственную подстановку .

Отсюда дифференцируя, получим . Возведем обе части уравнения в квадрат и воспользуемся подстановкой , отсюда или . Далее следуют преобразования

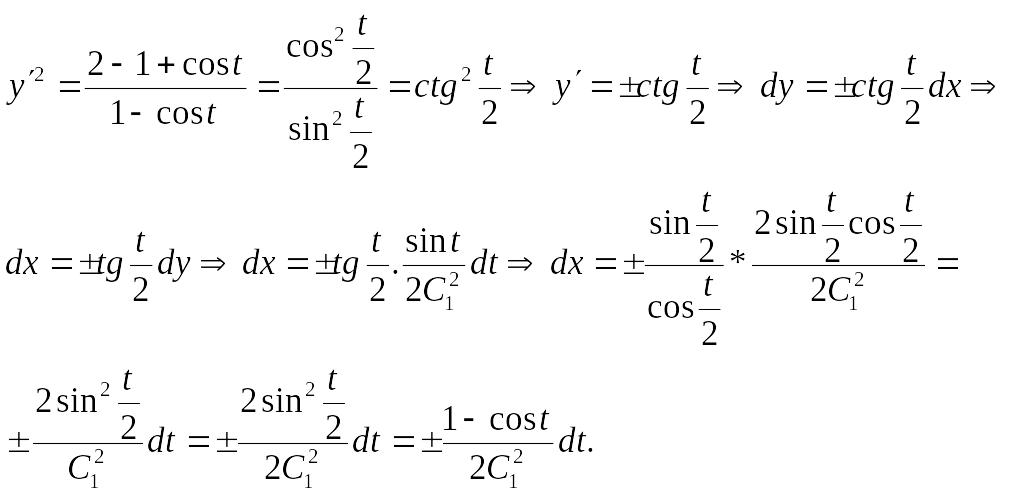
Следовательно, . (Знак можно не писать , т.к. t можно заменить на –t). Получим уравнение линии в параметрической форме

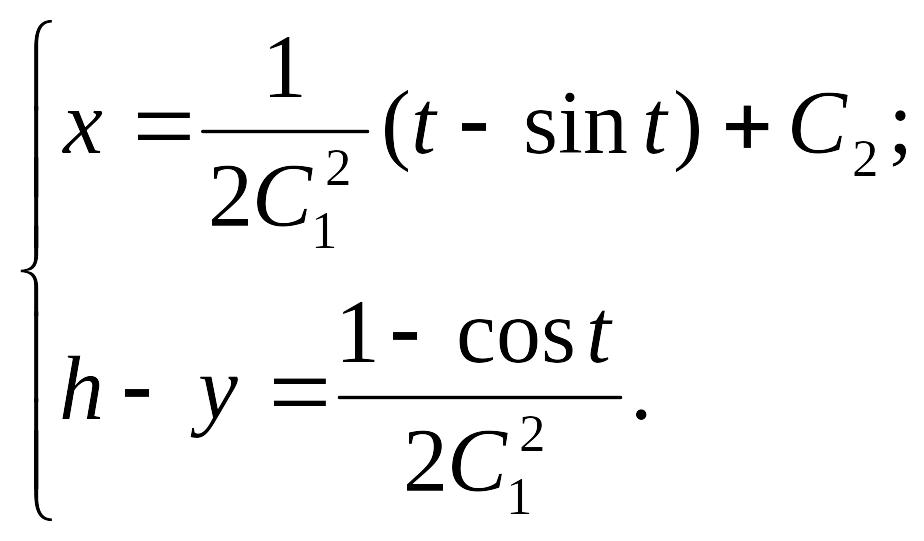
Так как линия должна пройти через точку (0;h) при t=0, то из первого уравнения видно, что =0. Получаем

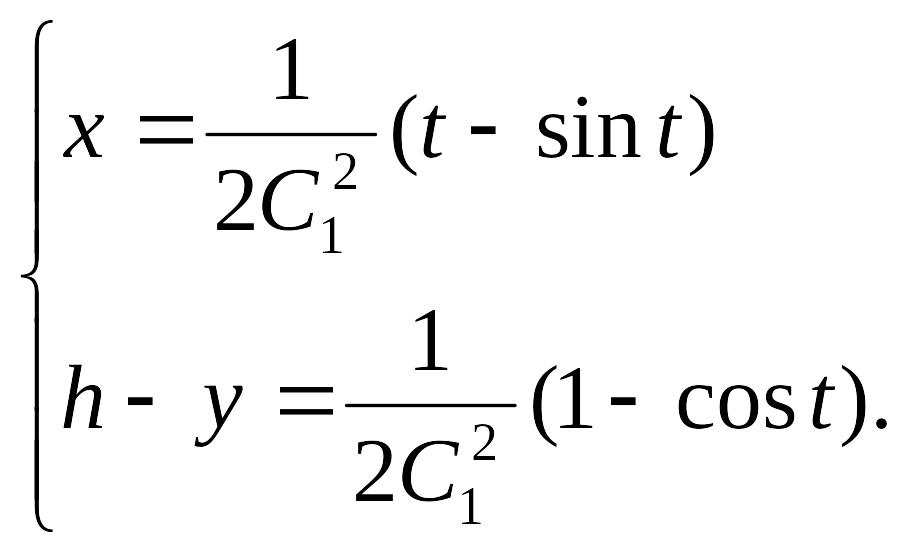
Эти уравнения определяют “перевёрнутую” циклоиду (семейство циклоид), получаемую при качении круга

По прямой y=h (рис.9).

Рис. 9

Значение R выбирается так, чтобы удовлетворить второму граничному условию, а именно, чтобы циклоида прошла через точку (b,0). Подставляя эти координаты в уравнения и, исключая t, можно получить трансцендентное уравнение для R.

Замечание. Если , тогда искомая линия частично проходит ниже точки финиша. Если трасса достаточно длинна, то выгодно сначала заглубить её, чтобы точка набрала достаточную скорость, быстро прошла трассу, а у финиша уже поднялась на требуемую высоту.