2. Первая вариация и необходимое условие экстремума

2.1. Приращения (вариация) аргумента функционала

Вариация аргумента функционала вводится по аналогии с приращением аргумента функции f(x). А именно,

Определение 1. приращением или вариацией аргумента y(x) функционала называется разность между двумя функциями . При этом предполагается, что y(x) меняется произвольно в некотором классе функций.

Определение 2. Функционал называется непрерывным, если малому изменению y(x) соответствует малое изменение функционала .

Данное определение аналогично определению непрерывности функции f(x): малому изменению x, соответствует малое изменение функции f(x).

Здесь следует уточнить, какие изменения функции y(x), являющейся аргументом функционала, считаются малыми или когда кривые и считаются близкими.

Можно считать близкими функции и в том случае, если мал для всех значений x, для которых задаются функции и . Это значит, что соответствующие кривые близки по ординатам.

Однако при таком определении близости кривых часто встречаемые в приложениях функционалы вида

из-за наличия в подынтегральной функции аргумента очень редко будут непрерывными. Поэтому во многих случаях естественно считать близкими только те кривые, которые близки по ординатам и по направлению касательных в соответствующих точках, т.е. требуется, чтобы были малы модули разностей не только функций , но и производных . Иногда требуется малость модуля разностей производных более высоких порядков.

Поэтому вводят следующие определения близости кривых и .

Кривые и называются близкими, в смысле близости нулевого порядка, если модуль разности мал.

Кривые и близки в смысле близости первого порядка, если модули разностей и малы. Кривые , близки в смысле к-го порядка, если модули разностей ; ; …; малы.

Н а рис. 4 изображены кривые, близкие в смысле близости нулевого порядка, но не близкие в смысле близости первого порядка, так как ординаты у них близки, а направления касательных не близки. На рис. 5 изображены кривые, близкие в смысле близости первого порядка.

Из этих определений следует, что если кривые близки в смысле к-го порядка, то они тем более близки в смысле близости любого меньшего порядка.

2.2. Вариация функционала

Линейным функционалом называется функционал ,

удовлетворяющий следующим условиям:

и

где с – производная постоянная.

Примером линейного функционала является

Для функций: линейной функцией называется функция , удовлетворяющая следующим условиям:

и .

Линейная функция одной переменной имеет вид , где k-постоянная.

Вариация функционала при изучении нелинейных функционалов играет ту же роль, что понятие дифференциала при изучении нелинейных функций. Если приращение функции может быть представлено в виде

,

где не зависит от , а при , то функция называется дифференцируемой, а линейная по отношению к часть приращения называется дифференциалом функции . Разделив на и переходя к пределу при , получим, что и, следовательно,

.

Определение. Если приращение функционала

можно представить в виде

, (1)

где -линейный по отношению к функционал, -максимальное значение и при , то называется вариацией функционала и обозначается . Если для краткости обозначить второе слагаемое в (1) через , то

, (2)

Таким образом, вариация нелинейного функционала равна главной линейной части его приращения. Замена приращения на вариацию означает линеаризацию функционала при переходе от одной функции к другой, близкой функции .

Здесь -произвольная функция, мало уклоняющаяся от нуля и добавляемая к исходной функции для получения новой функции (рис. 6).

Пример 1. Дан функционал . Найти его вариацию.

Решение. При переходе от к функционал получит приращение

.

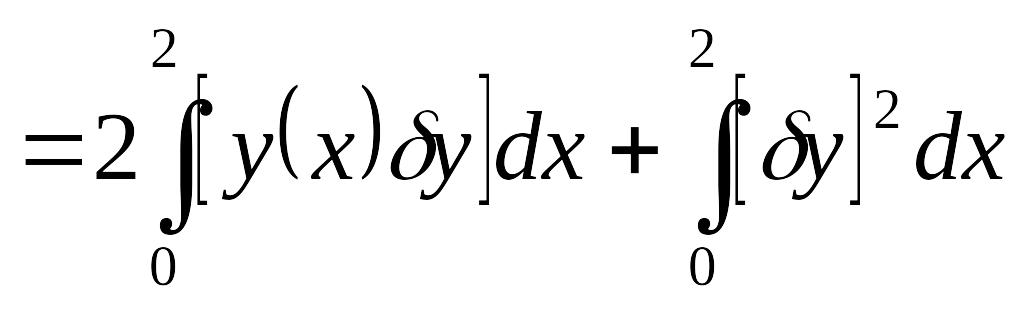При фиксированной функции функционал состоит из двух частей. Каждая из этих частей представляет собой функционал относительно . Первое слагаемое есть линейный функционал относительно , а второе слагаемое при малых имеет высший порядок малости. Таким образом,

.

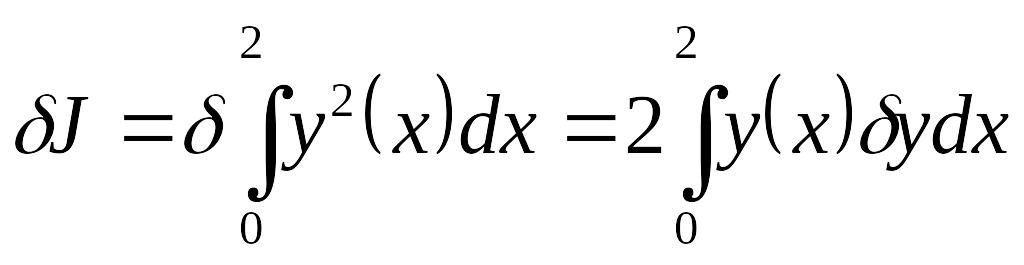В конкретных задачах вариация функционалов вычисляется с помощью формулы Тейлора. Так, для функционала вида

, (3)

где при интегрировании считается , имеет

. (*)

Т.к. высшего порядка, то подставляя в (*) и отбрасывая эти члены, получим

. (4)

Для функционала

(5)

аналогично получаем

, (6)

где можно понимать и как , и как , т.к. (производная от разности двух функций равна разности производных).

Действительно, высшего порядка.