3.1. Пример выполнения задачи № 1
Пусть
10
кН;
-20 кН;
30 кН*м;
-10 кН/м.
Р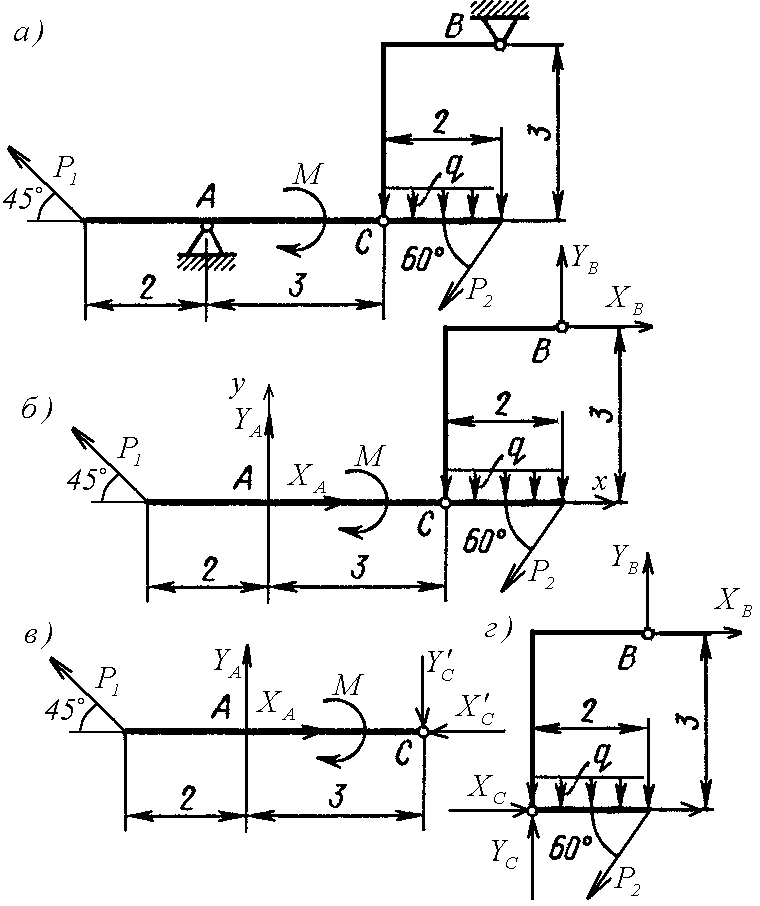
асчетная
схема системы приведена на рис. 1.1, а.
Рис. 1.1
Решение
1. Система сил, приложенных к конструкции плоская, поэтому для нее можно записать три уравнения равновесия.
Для упрощения вычислений рекомендуется разложить силы и на составляющие вдоль осей х и у и определить их проекции
-10*0,707=
-7,070 кН;
10*0,707=
7,070 кН.
-20*(-0,5)=
10 кН;
-20*(-0,866)=
17,332 кН.
Отбрасывая
опоры конструкции, заменяем их действие
на конструкцию реакциями
и
(рис. 1.1, б), которые раскладываем на
составляющие
и
,
и
.
Уравнения равновесия всей конструкции имеют вид
,
;
,
; (1.1)
,
.
2.
Уравнение равновесия моментов сил для
стержня
относительно точки С имеет вид
,
.
Из этого уравнения получаем
-(5*(10*0,707+30)/3=
-21,783 кН.
Из второго уравнения (1.1)получаем
-(-21,783+7,070-2*(-10)-
-20*0,866)= 12,033 кН.
Из третьего уравнения (1.1) получаем
= (5*12,033-30-2(-10)*4-7,070*2-17,332*5)/3= 3,1216 кН.
Из первого уравнения (1.1) получаем
-(3,1216-7,070-10)= 13,948 кН.
Полная реакция в шарнире A
25,866
кН.
Угол,
образуемый
с осью х
.
Полная реакция в шарнире В
12,431
кН.
Угол,
образуемый
с осью х
.
4.
Разъединяем конструкцию по шарниру С,
изображаем по отдельности ее части и
прикладываем к ним реакции
и
,
которые раскладываем на составляющие
и
,
и
.
5. Уравнения равновесия части конструкции, расположенной левее точки С в проекциях на ось х и у имеют вид
,
;
,
.
Из этих уравнений следует
13,948-7,070=
6,878 кН;
-21,783+7,070=
-14,703 кН.
Полная реакция в шарнире С
16,232
кН.
Угол,
образуемый
с осью х
.
6.
Уравнения равновесия стержня
в проекциях на ось х и у имеют вид
,
;
,
.
Из этих уравнений следует
-(3,1216-10)=
6,878 кН;
-12,033+2*(-10)+17,332=
-14,701 кН.
Полная реакция в шарнире С
=
16,232 кН.
Поскольку
и
,
реакция в шарнире С определена правильно.
Таблица результатов вычислений
Обозначение реакции |
Модуль |
Проекция на ось х |
Проекция на ось у |
Угол, образуемый с остью х в град |
|
25,866 |
13,948 |
-21,783 |
296,258 |
|
12,431 |
3,122 |
12,033 |
85,032 |
|
16,232 |
6,878 |
-14,701 |
287,855 |
4. Выбор вариантов исходных данных для
ЗАДАЧ 2 - 7
Информация для выполнения задач 2 - 7 определяется по последним трем цифрам номера N зачетной книжки студента. Пусть K, L и М три последних цифры номера N, перечисленные в порядке слева направо. Пусть, например, зачётная книжка имеет номер 10195. Тогда K= 1, L= 9, M= 5. Номер варианта числовых данных ко всем задачам, за исключением задачи 7, выбирается по последней цифре номера M. Более подробные инструкции по выбору исходной информации к задачам приведены в условиях каждой из задач.
5. Задача №2
Р
АСТЯЖЕНИЕ
И СЖАТИЕ СТУПЕНЧАТОГО СТЕРЖНЯ
С
Рис.
2.1
.
Требуется:
а) раскрыть статическую неопределимость системы;
б)
построить эпюры нормальных сил N
и нормальных напряжений
при
заданных значениях распределенной
нагрузки
и сосредоточенных сил;
в)
определить перемещение точки приложения
сосредоточенной силы
.
г)
построить эпюру температурных напряжений
при отсутствии нагрузок, если известно,
что температура стержня в процессе
работы изменилась на
;
Числовые данные к задаче 2 взять из таблицы 2.1, где все линейные величины даны в метрах, площади сечений стержней в см2, изменение температуры в градусах Кельвина, силы в кН.
Направления
распределенной нагрузки или сосредоточенной
силы определяются числом
.
При четном
сосредоточенная сила или распределенная
нагрузка направлены в соответствии с
данными таблицы 2.1 и рисунком 2.1. При
нечетном
направления этих нагрузок противоположны
направлениям, указанным на этом рисунке.
Таблица 2.1
№ п/п |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1,0 |
2 |
1 |
1,5 |
2 |
2 |
- |
- |
3 |
- |
- |
-20 |
1 |
0,9 |
3 |
0,5 |
1 |
3 |
- |
3 |
- |
- |
2 |
- |
+30 |
2 |
0,8 |
4 |
0,8 |
2 |
1,2 |
- |
- |
1 |
- |
- |
1 |
-40 |
3 |
0,7 |
5 |
2 |
1 |
3 |
1 |
- |
- |
2 |
- |
- |
+50 |
4 |
0,6 |
6 |
3 |
0,8 |
2 |
- |
3 |
- |
- |
3 |
- |
-30 |
5 |
0,5 |
7 |
1,5 |
2 |
1 |
- |
- |
2 |
- |
- |
2 |
+60 |
6 |
1,2 |
8 |
1,2 |
1 |
1,5 |
3 |
- |
- |
2 |
- |
- |
-40 |
7 |
1,1 |
9 |
0,6 |
1 |
1,8 |
- |
2 |
- |
- |
2 |
- |
+45 |
8 |
1,4 |
5 |
0,8 |
1,5 |
2 |
- |
- |
1 |
- |
- |
1 |
-55 |
9 |
1,5 |
4 |
2 |
1,5 |
0,8 |
2 |
- |
- |
3 |
- |
- |
+60 |
Если в соответствующей ячейке таблицы находится прочерк, то это указывает на отсутствие соответствующей силы или распределенной нагрузки.
Принять
1 м, значение модуля упругости для стали
равным
2,0*105
МПа, а коэффициент температурного
расширения равным
125*10-7
1/м. Площади участков стержня определять
по формулам,
.
Распределенные нагрузки и сосредоточенные
силы определять по формулам
,
.
Прочие исходные данные взять из табл.
2.1.