
- •230104 «Системы автоматизированного проектирования»,
- •230101 «Вычислительные машины,
- •§1. Возрастание и убывание функции.
- •§2. Экстремумы функции
- •§3. Выпуклость и вогнутость. Точки перегиба
- •§4. Асимптоты
- •§5. Построение графика функции
- •§6. Наибольшее и наименьшее значения
- •§7. Элементарные преобразования графиков
- •Задание 1.
- •Задание 2.
- •§1. Возрастание и убывание функции…………1
- •230104 «Системы автоматизированного
- •230101 «Вычислительные машины, комплексы,
- •394026 Воронеж, Московский просп., 14
§3. Выпуклость и вогнутость. Точки перегиба
Дифференцируемая функция y = f(x) называется выпуклой (вогнутой) или выпуклой вверх (вниз) на интервале (a; b), если она удовлетворяет следующему условию: для любых различных точек
x1,
x2(a;
b) часть графика функции
y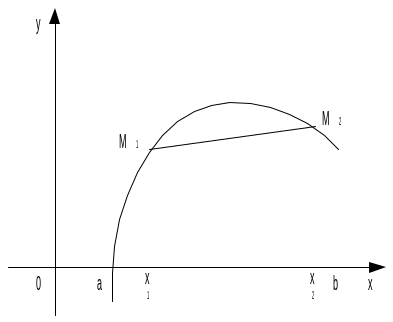 = f(x),
соответствующая интервалу (x1;
x2), расположена
выше (ниже) отрезка M1M2,
где M1(x1;
f(x1)),
M2(x2;
f(x2)).
= f(x),
соответствующая интервалу (x1;
x2), расположена
выше (ниже) отрезка M1M2,
где M1(x1;
f(x1)),
M2(x2;
f(x2)).
Т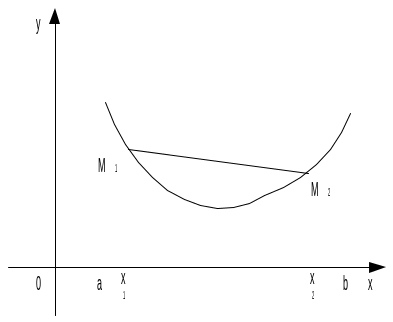 очка
графика функции, разделяющая выпуклый
и вогнутый участки графика, называется
точкой перегиба (часто точкой
перегиба называют абсциссу этой точки
графика функции).
очка
графика функции, разделяющая выпуклый
и вогнутый участки графика, называется
точкой перегиба (часто точкой
перегиба называют абсциссу этой точки
графика функции).
Теорема 4. Если для функции f(x)
, дважды дифференцируемой в (a;
b),
![]() (
(![]() )
при всех x(a;
b), то функция f(x)
является выпуклой (вогнутой) на (a;
b) .
)
при всех x(a;
b), то функция f(x)
является выпуклой (вогнутой) на (a;
b) .
Теорема 5. Пусть функция f(x)
дважды дифференцируема на (a;
b). Точка x0(a;
b) является точкой перегиба
в том и только в том случае, если
одновременно выполняются два условия:
1)
![]() ;
2) при переходе через точку x0
;
2) при переходе через точку x0
![]() меняет свой знак.
меняет свой знак.
В последней теореме при условии трижды дифференцируе-
мости
функции условие 2) можно заменить на
![]() .
.
Пример 3.1. Найти точки перегиба и интервалы выпуклости и вогнутости для функции .
Решение.
Найдем вторую производную
![]() .
.
Очевидно,
критические точки
![]() и
и
![]() не
существует). При переходе через точку
не
существует). При переходе через точку
![]()
![]() меняет знак. Значит
– точка перегиба. При переходе через
точку
меняет знак. Значит
– точка перегиба. При переходе через
точку
![]() знака не меняет, следовательно, в этой
точке перегиба нет.
знака не меняет, следовательно, в этой
точке перегиба нет.
Исследование удобно оформить в виде таблицы.
Интервал |
|
1 |
|
|
|
f(x) |
выпукла вверх |
|
выпукла вверх |
|
выпукла вниз |
|
<0 |
|
<0 |
0 |
>0 |
|
|
|
|
Точка перегиба |
|
Используя информацию из таблицы, уточним график функции.
Можно убедиться в том, что график функции не имеет асимптот.
Пример
3.2.
Найти точки перегиба и интервалы
выпуклости и вогнутости для функции
![]()
Решение.
Найдем вторую производную
![]()
Производная
![]() нигде в нуль не обращается. Приравнивая
к нулю знаменатель дроби, получаем
нигде в нуль не обращается. Приравнивая
к нулю знаменатель дроби, получаем
![]() ,
откуда
.
В точке
вторая производная не существует (
,
откуда
.
В точке
вторая производная не существует (![]() ).
Исследуем знак второй производной слева
и справа от точки
).
Исследуем знак второй производной слева
и справа от точки
![]() для
для
![]() .
Точек перегиба нет,
.
Точек перегиба нет,
![]() интервал вогнутости.
интервал вогнутости.
Задачи для самостоятельного решения.
Найти
интервалы выпуклости, вогнутости и
точки перегиба графика функции
![]() :
:
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]()
6.
При каких значениях a
и b
точка (1,3) является точкой перегиба
кривой
![]() ?
?
Ответы: 1. График функции всюду вогнут;
2.
![]() выпуклый,
выпуклый,
![]() вогнутый, (2,0)- точка перегиба;
вогнутый, (2,0)- точка перегиба;
3. График функции всюду вогнут;
4.
![]() выпуклый,
выпуклый,
![]() вогнутый, М(-1, 1-
вогнутый, М(-1, 1-![]() -
точка перегиба;
-
точка перегиба;
5.
![]() выпуклый,
выпуклый,
![]() вогнутый,
вогнутый,
![]() -
точка перегиба;
-
точка перегиба;
6.
![]()
§4. Асимптоты
Прямая (L) называется асимптотой графика функции (или просто асимптотой функции), если расстояние d(M; (L)) от точки М на графике функции y = f(x) до прямой (L) стремится к 0 при неограниченном удалении точки М от начала координат.
Различают два вида асимптот: вертикальные и наклонные.
Прямая x = x0 является вертикальной асимптотой, если по крайней мере один из односторонних пределов f(x0 – 0),
f(x0 + 0) равен - или +.
Например, прямая
![]() является вертикальной асимптотой
графиков функций
является вертикальной асимптотой
графиков функций
![]() и
и
![]() ,
так как
,
так как
![]() и
и
![]() .
График функции
.
График функции
![]() имеет бесконечно много вертикальных
асимптот, а именно, каждая прямая
имеет бесконечно много вертикальных
асимптот, а именно, каждая прямая
![]() ,
является вертикальной асимптотой.
,
является вертикальной асимптотой.
Пример 4.1. Найти вертикальные асимптоты функции
![]() .
.
Решение.
Точки разрыва нашей функции
![]() .
Проверим, являются ли прямые
и
.
Проверим, являются ли прямые
и
![]() вертикальными асимптотами. Имеем
вертикальными асимптотами. Имеем
![]() ,
,
![]() .
Согласно определению, прямая x=1
является
вертикальной асимптотой. Аналогично,
прямая
является вертикальной асимптотой.
.
Согласно определению, прямая x=1
является
вертикальной асимптотой. Аналогично,
прямая
является вертикальной асимптотой.
Наклонная асимптота y = kx + b соответствует случаю
x – или x + . Коэффициенты k и b при x + находятся из равенств
![]() ,
,
![]()
(то же при x – ). Если же не существует одного из пределов или один из этих пределов равен – или + , то у функции отсутствует наклонная асимптота при x + (то же при x – ).
Если
![]() ,
то асимптоту
,
то асимптоту
![]() называют горизонтальной.
называют горизонтальной.
Пример 4.2.
Найти наклонные асимптоты функции
![]() .
.
Решение. По формулам (3) имеем
![]() ,
,
![]() .
Следовательно, график нашей функции
имеет две асимптоты
.
Следовательно, график нашей функции
имеет две асимптоты
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Пример
4.3. Найти
асимптоты графика функции
![]()
Решение.
Функция определена при
![]() Так
как
Так
как
![]() ,
то
прямая
является вертикальной асимптотой. Так
как
,
то
прямая
является вертикальной асимптотой. Так
как
![]() ,
имеем
,
имеем
![]()
Следовательно, наклонной асимптоты нет.
Пример
4.4. Найти
асимптоты графика функции
![]()
Решение.
Функция определена при
![]() Так
как
Так
как
![]() и
и
![]() ,
то
прямые
и
,
то
прямые
и
![]() являются вертикальными асимптотами.
Находим наклонные асимптоты. При
,
получаем
являются вертикальными асимптотами.
Находим наклонные асимптоты. При
,
получаем
![]()

следовательно,
правой наклонной асимптотой является
прямая
![]() Аналогично,
при
,
имеем
Аналогично,
при
,
имеем
![]() .
.
Таким
образом, левой наклонной асимптотой
является прямая
![]()
Замечание.
Исследование упрощается, если учесть
четность функции, а значит симметрию
графика функции относительно оси
![]() .
.
Задачи для самостоятельного решения.
Найти асимптоты графиков функций:
1.
![]() 2.
2.
![]() 3.
3.
![]() ;
;
4.![]() 5.
5.
![]()
Ответы:
1.
![]() 2.
2.
![]() 3.
3.
![]() -правая,
-правая,
![]() -
левая; 4.
-
левая; 4.
![]() -
левая;
-
левая;
5.
![]()
