Примеры решения задач из типового расчета
Пример 1.
Используя
формулы Крамера решить систему
уравнений
Решение.
Главный определитель данной системы
,
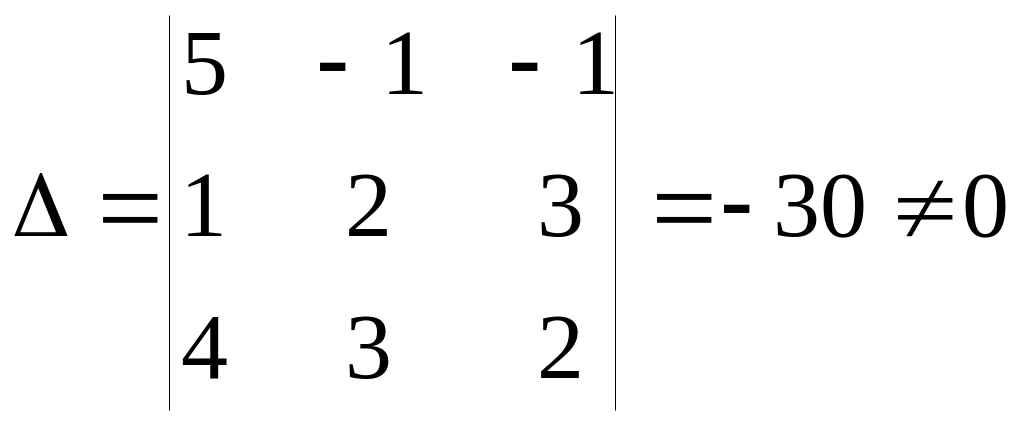поэтому, система имеет единственное
решение, определить которое возможно
после вычисления вспомогательных
определителей
,
и
:
=
,
=
,
=
.
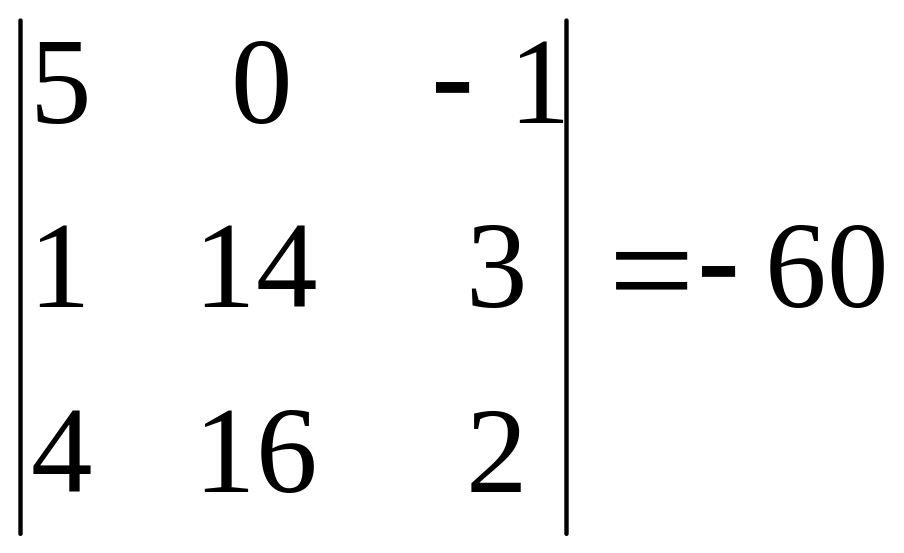По
формулам Крамера:
,
,
.
Задача 2. Даны три точки А(4;2), В(-1;-3), С(6;1). См. задания задачи 2.
Решение.
а)
Векторы
,
имеют координаты
,
и их длины
,
.
б) Косинус угла между векторами , определяется формулой:
.
в)
Проекция вектора
на
:
.
г)
Изобразим на плоскости векторы
,
,
,
.
Рис. 18
Задача 3. Даны три точки А(4;2), В(-1;-3), С(6;1). См. задания задачи 3.
Решение.
Д
ля
определения уравнений сторон АВ, АС
воспользуемся формулой
,
тогда уравнение стороны АВ:
,
т.е.
,
а уравнение стороны АС:
,
т.е.
.
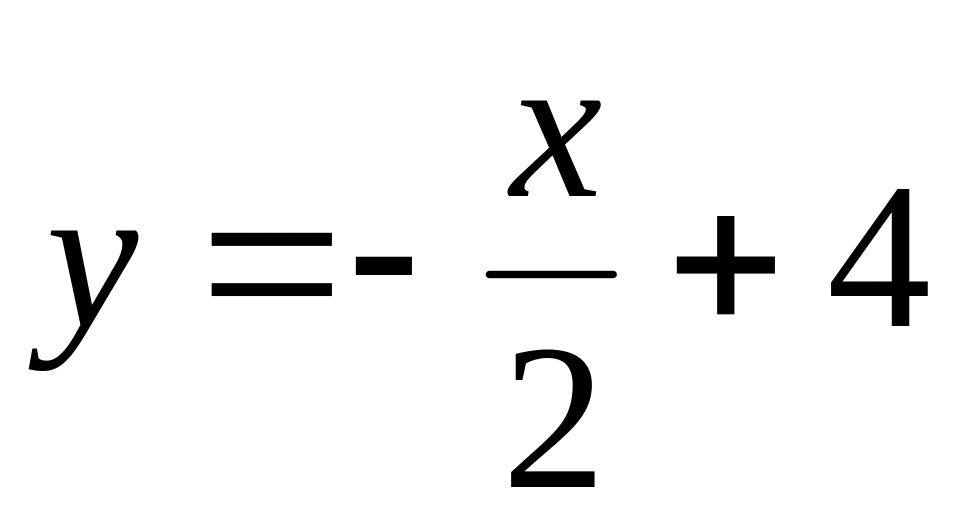Угловые коэффициенты прямых
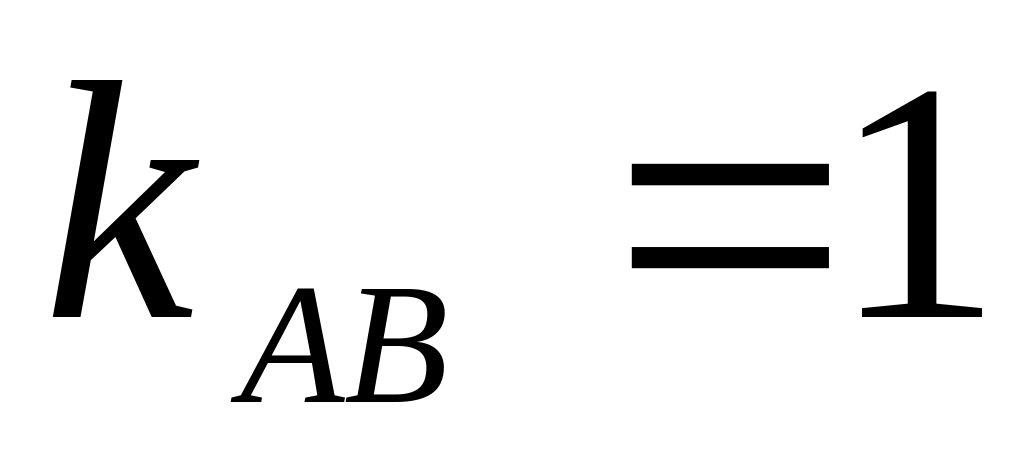и
,
тогда угол между ними определяется из
формулы
.
Т.к. из чертежа видно, что угол
при вершине
А
тупой, то
.Д
Рис.19
ля определения высоты АН, заметим, что она перпендикулярна стороне ВС, тогда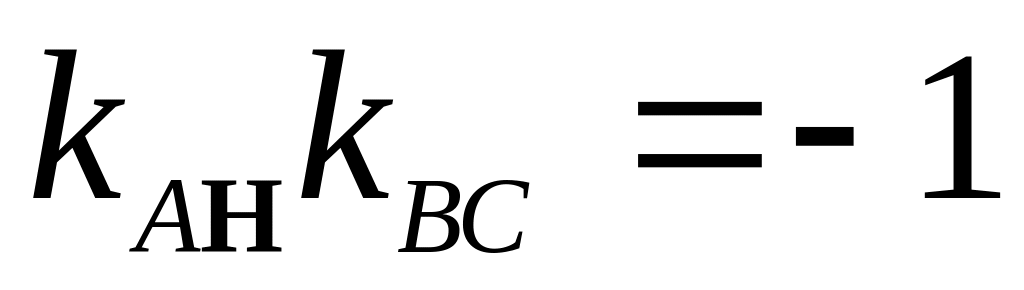
.
Определим уравнение стороны ВС:
,
поэтому
.
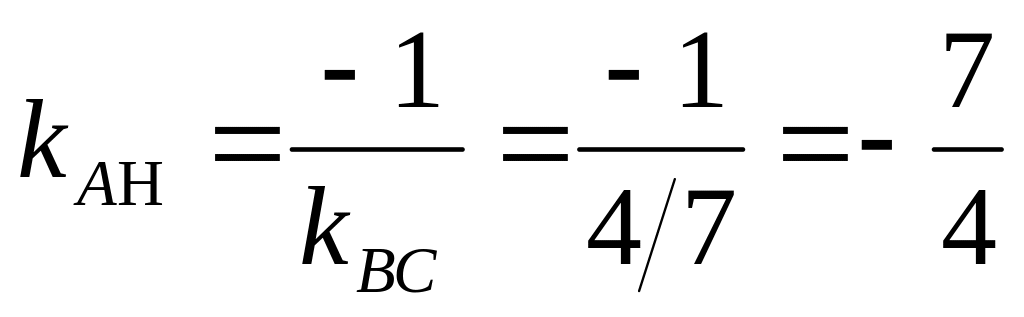Уравнение высоты, проходящей через
точку А, можно определить,
воспользовавшись уравнением
,
в которое подставим координаты точки
А и угловой коэффициент. Итак,
уравнение высоты АН имеет вид
.
Для определения длины высоты приведем
уравнение ВС к общему виду
и воспользуемся формулой
,
тогда
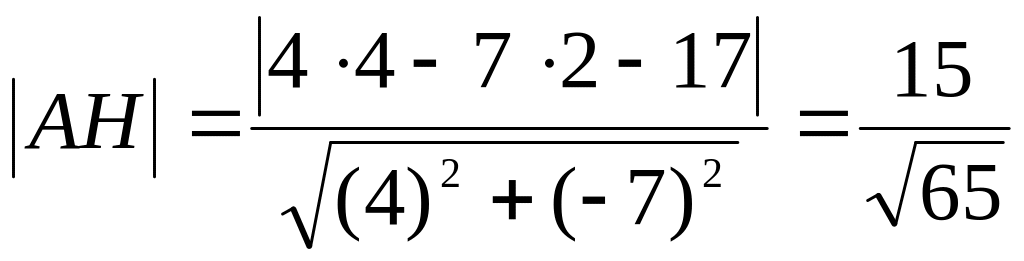.Заметим, что точка М есть середина ВС, поэтому
,
.
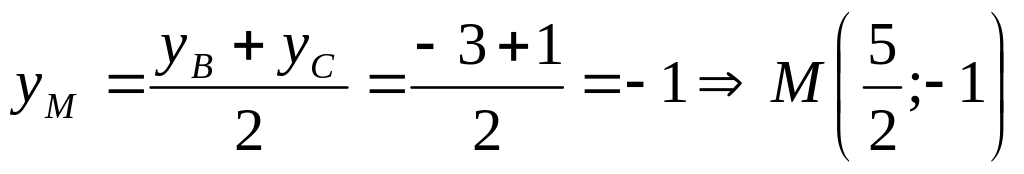Соответственно, уравнение медианы АM
имеет вид
,
т.е.
.Площадь треугольника
.
Длина высоты
определена в пункте 2. Определим длину
стороны ВС по формуле
.
Итак,
.Центр описанной окружности, находится в точке пересечения серединных перпендикуляров сторон (задание для самостоятельной работы).
Искомая прямая l проходит через точку А(4;2) параллельно ВС, поэтому
.
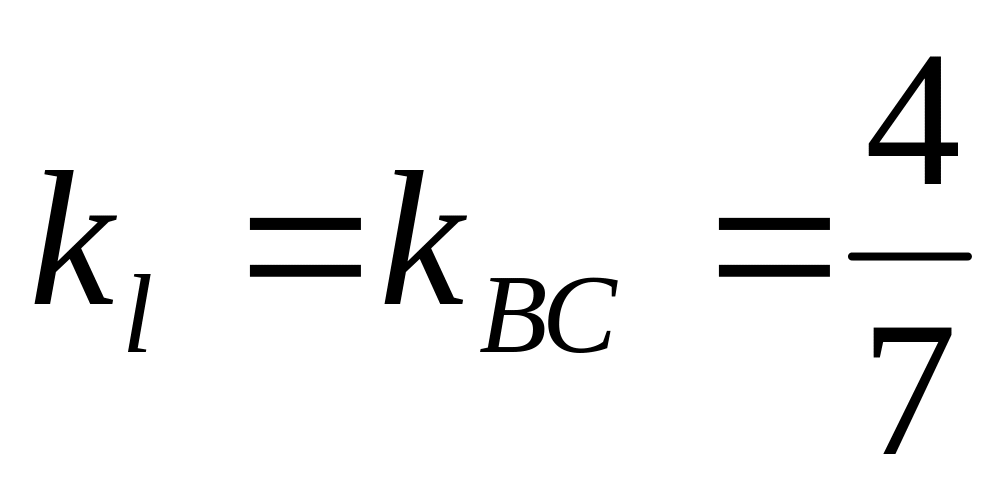Воспользуемся уравнением
:
,
получим уравнение прямой l:
.
Задача 4. Пирамида ABCD задана вершинами А(1;2;-3), В(2;-4;1), С(-3;-5;-1), D(-2;0;5). См. задания задачи 4.
Решение.
1) Воспользуемся уравнением плоскости
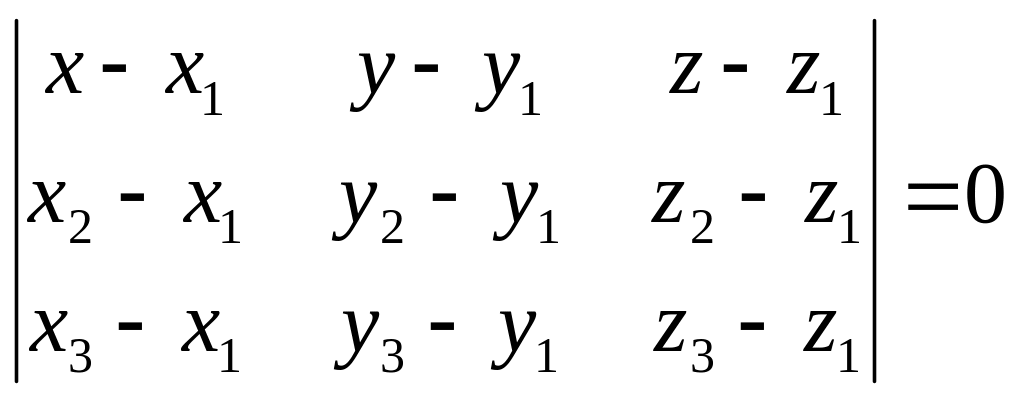и составим уравнение грани
,
.
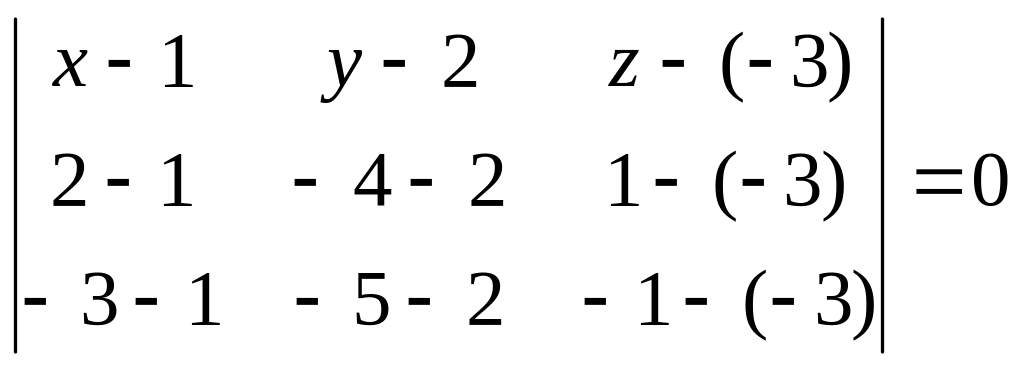Раскрыв определитель, получаем общее
уравнение плоскости, содержащей точки
,
и
:
,
нормальный вектор которой
.
Аналогично
получено уравнение грани
с нормальным вектором
.
Угол
между плоскостями равен углу между их
нормальными векторами
и
плоскостям, т.е.
.
Воспользуемся уравнениями прямой
и составим уравнения прямой
:
,
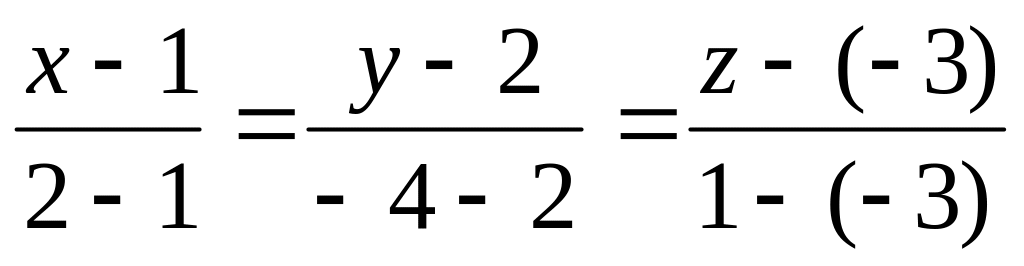
направляющий вектор которой
.
Аналогично получен вектор
.
Угол между прямыми
,
равен углу между векторами
и
:
,
т.е.
.
3) Угол между
плоскостью АВС с нормальным вектором
и прямой
с направляющим вектором
определяется формулой
,
значит
.
4) Длина высоты
пирамиды, опущенной из точки D(-2;0;5)
равна расстоянию от точки D
до плоскости ABC (
)
и определяется формулой
.
5) Площадь грани
равна площади треугольника с заданными
вершинами и вычисляется по формуле
,
где
,
.
Заметим, что:
,
где
,
тогда
.
Итак,
(кв.ед.).
6) объем пирамиды
вычисляется по формуле
,
где площадь основания пирамиды
,
высота пирамиды
найдена в п. 4.
Таким образом,
(куб.ед.).
Задача 5. Привести
уравнение кривой
к каноническому виду и построить кривую
в системе координат xOy.
Решение. Выделим в левой части уравнения кривой полные квадраты по каждой из переменной:
Т
Рис.20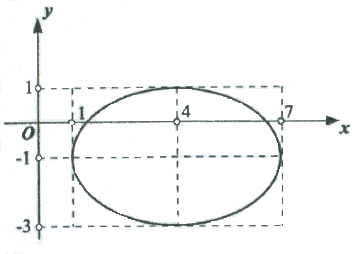
Делим обе его части на 36:
Введем замену переменных
,
,
получим уравнение кривой
,
которое является уравне-нием эллипса
с полуосями
,
и центром в точке
.
(Рис. 20).
Задача 6. Определить
типы поверхностей по их уравнениям и
изобразить поверхности схематически
в системе координат Oxyz:
a)
,
б)
.
Решение.
a)
Запишем уравнение в виде:
,
разделив обе его части на (-36). Сравнивая
это уравнение с каноническими уравнениями
второго порядка, видим, что это уравнение
конуса, ось которого – Ox
(рис.21).
б) Заданное уравнение не содержит переменной y, поэтому оно задает цилиндр в направлении оси Oy, направляющей линией которого является парабола – это параболический цилиндр (см. рис.22).
Рис. 21 Рис. 22
Пример
7. Найти производную функции
.
Решение. Функция является произведением функций, одна из которых сложная:
Пример
8. Исследовать функцию
и построить ее график.
Решение.
1. Областью
определения данной функции, которая
является многочленом, будет вся числовая
ось
.
2. Найдем точки пересечения графика с осями координат:
с осью Oy
(при x=0):
;
с осью Ox
(при y =0):
и
.
3. Функция не является периодической, см. п.2.
Функция не является ни четной, ни нечетной, т к.
,
т.е.
и
.
3. Найдем точки возможного экстремума функции, определив при каких x обращается в ноль или не определена первая производная функции:
,
тогда
при
и при
.
4. Найдем точки возможного перегиба функции, определив при каких x обращается в ноль или не определена вторая производная функции:
,
тогда
при
.
5. Составим таблицу,
в которую будут включены все критические
точки:
,
,
.
Далее будут проверены достаточные
условия существования перегиба и
экстремума в данных точках.
|
|
-2 |
|
-1 |
|
0 |
|
|
|
4
|
|
2
|
|
0
|
|
|
|
0
|
|
|
|
0
|
|
|
max |
|
|
|
min |
|
|
|
|
|
|
0
|
|
|
|
|
|
|
перегиб |
|
|
|
Д
ля
построения графика:
укажем в системе координат все точки определенные в п. 2 и в п. 5.;
н
Рис.23
а каждом из промежутков
,
,
и
построим график функции, руководствуясь
таблицей и точками графика
,
,
,
.
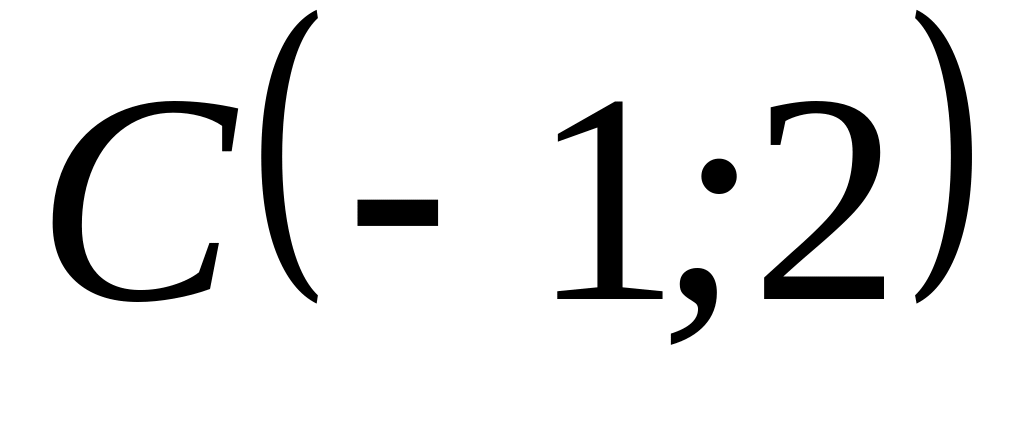Пример
9. Составим уравнение касательной и
нормали к графику функции
в точке с абсциссой
.
Решение.
Значение функции
в точке с абсциссой
равно
,
а значение производной
в той же точке
равно
.
Поэтому уравнения
касательной
и уравнение нормали
имеют, соответственно, вид
(касательная) и
(нормаль).