Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Файл:

Аналитическая геометрия. Дифференциальное исчисление. методические указания и задания по математике. Дементьева А.М., Акчурина Л.В.doc

Скачиваний:

Добавлен:

30.04.2022

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Задания к типовому расчету №1 Системы линейных уравнений. Аналитическая геометрия

Задача 1. Решить систему уравнений а) методом Гаусса; б) методом Крамера.

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.

Задача 2. Даны три точки А, В и С найти: а) координаты векторов , и их длины; б) найти косинус угла между векторами , ; в) найти проекцию вектора на ; г) построить на координатной плоскости векторы , , , .

1.	А(4;-3),	В(2;4),	С(-1;2);	16.	А(-6;2),	В(2;3),	С(1;-4);
2.	А(-3;-2),	В(5;1),	С(1;-4);	17.	А(-3;-4),	В(-1;3),	С(4;1);
3.	А(1;5),	В(-3;2),	С(1;3);	18.	А(-1;-3),	В(-6;2),	С(2;3);
4.	А(-3;-2),	В(-1;4),	С(4;2);	19.	А(5;3),	В(-4;2),	С(3;-4);
5.	А(-5;1),	В(-1;2),	С(-3;-2);	20.	А(4;-3),	В(-3;-4),	С(-1;4);
6.	А(1;-4),	В(5;-1),	С(-2;3);	21.	А(-4;-4),	В(3;3),	С(5;-2);
7.	А(1;-2),	В(4;1),	С(0;4);	22.	А(-6;-1),	В(5;2),	С(-1;1);
8.	А(-1;-4),	В(4;1),	С(-1;2);	23.	А(-1;-5),	В(1;-3),	С(-2;6);
9.	А(-3;2),	В(2;3),	С(-1;-4);	24.	А(-4;1),	В(4;-1),	С(1;-2);
10.	А(-1;3),	В(4;1),	С(0;-3);	25.	А(-1;5),	В(6;1),	С(1;-1);
11.	А(4;0),	В(-1;-3),	С(-2;-6);	26.	А(-6;-2),	В(-1;8),	С(6;1);
12.	А(-4;0),	В(2;3),	С(1;-2);	27.	А(-3;3),	В(5;6),	С(1;-4);
13.	А(-3;1),	В(2;2),	С(0;-2);	28.	А(-4;4),	В(-1;-5),	С(4;-2);
14.	А(4;2),	В(-2;3),	С(1;-2);	29.	А(2;2),	В(-4;3),	С(-1;-6);
15.	А(5;1),	В(1;6),	С(-2;0);	30.	А(-3;-4),	В(6;1),	С(2;-6).

Задача 3. Для треугольника АВС (координаты вершин которого заданы в задаче 2) определить:

уравнения сторон АВ, АС и угол между ними;
уравнение и длину высоты АН, опущенной из вершины А;
уравнение медианы АМ;
площадь треугольника;
центр описанной окружности, построить треугольник в системе xOy, указать центр и окружность на чертеже (задание для самостоятельного изучения).
уравнение прямой l проходящей через точку А, параллельно ВС.

Задача 4. Для пирамиды заданной вершинами определить:

уравнения граней 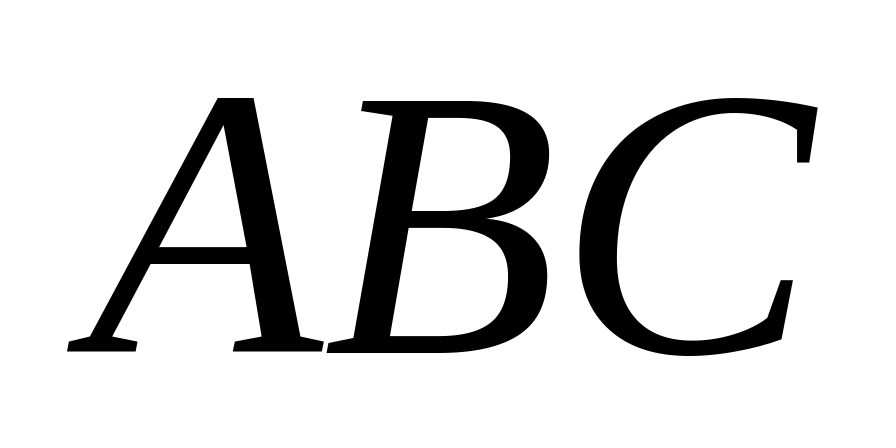, 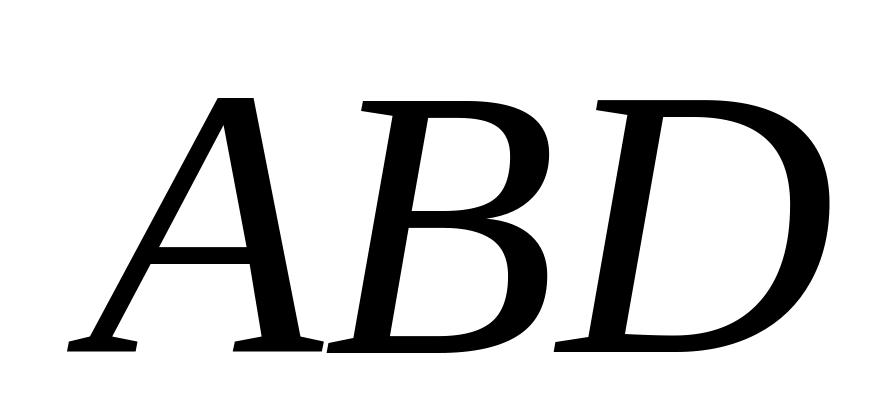и косинус угла между ними;
уравнения ребер 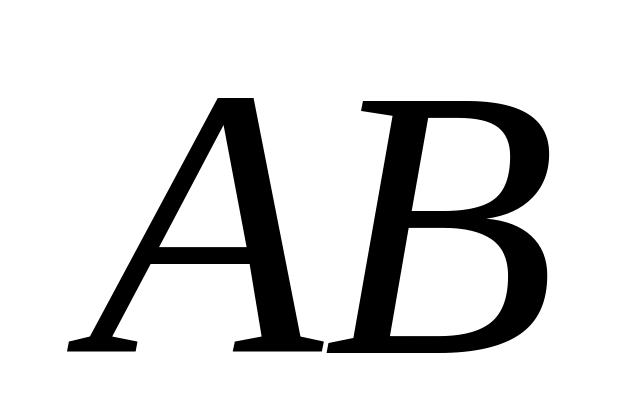, и косинус угла между ними;
синус угла между гранью 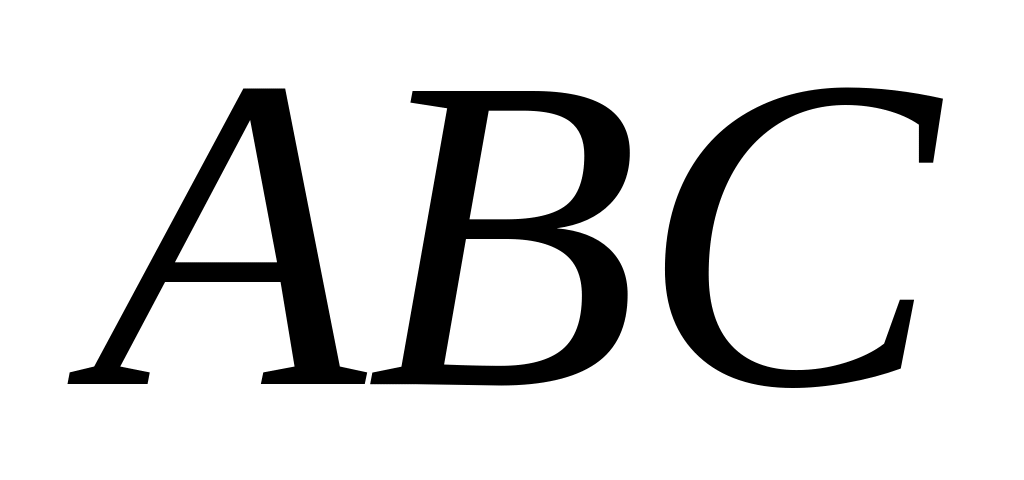и ребром ;
длину высоты пирамиды, опущенной из точки ;
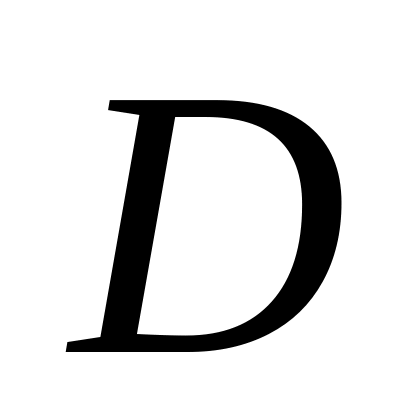площадь грани ;
объем пирамиды.

Варианты:

1.	(4,2,5),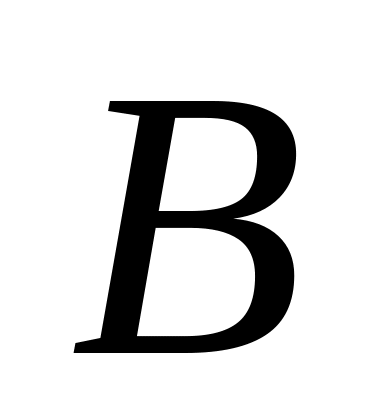	(0,7,2),	(0,2,7),	(1,5,0);
2.	(4,4,10),	(4,10,2),	(2,8,4),	(9,6,4);
3.	(4,6,5),	(6,9,4),	(2,10,10),	(7,5,9);
4.	(3,5,4),	(8,7,4),	(5,10,4),	(4,7.8);
5.	(10,6,6),	(-2,8,2),	(6,8,9;),	(7,10,3);
6.	(1,8,2),	(5,2,6),	(5,7,4),	(4,10,9);
7.	(6,6,5),	(4,9,5),	(4,6,11),	(6,9,4);
8.	(7,2,2),	(5,7,7),	(5,6,8),	(8,10,7);
9.	(8,6,4),	(10,5,5),	(5,3,1),	(2,3,7);
10.	(7,7,3),	(6,5,8),	(3,5,8),	(8,4,1);
11.	(3,5,4),	(5,8,3;),	(1,9,9),	(6,4,8);
12.	(9,5,5),	(-3,7,1),	(5,7,8),	(6,9,2);
13.	(0,7,1),	(4,1,5),	(4,6,3),	(3,9,8);
14.	(6,1,1),	(4,6,6),	(4,2,0),	(1,2,6);
15.	(2,4,3),	(4,7,2),	(0,8,8),	(5,8,1);
16.	(8,4,4),	(-4,6,0),	(4,6,7),	(5,8,1);
17.	(-1,6,0),	(3,0,4),	(3,5,2),	(0,1,5);
18.	(5,0,1),	(3,5,5),	(3,1,-1),	(2,8,7);
19.	(1,-1,2),	(-3,4,-1),	(-3,-1,4),	(-2,2,3);
20.	(1,3,2),	(3,6,1),	(-1,7,7),	(4,2,6);
21.	(-2,5,-1),	(2,4,4),	(2,4,1),	(1,7,6);
22.	(4,-1,1),	(2,1,3),	(2,4,1),	(4,7,0);
23.	(0,2,1),	(2,5,0),	(-2,6,6),	(3,1,5);
24.	(6,2,2),	(-6,4,2),	(2,4,5),	(3,6,-1);
25.	(-3,4,-2),	(1,-2,2),	(1,3,0),	(0,6,5);
26.	(1,4,7),	(-2,4,1),	(-4,0,2),	(8,-1,5);
27.	(1,5,0),	(0,2,7),	(0,7,2),	(4,2,5);
28.	(9,6,4),	(2,8,4),	(4,10,2),	(3,4,10);
29.	(7,5,9),	(2,7,10),	(6,9,4),	(4,6,5);
30.	(4,7,8),	(5,10,4),	(8,7,4),	(3,5,4);

Задача 5. Определить вид кривой приведением их уравнений к каноническому виду. Построить кривые в системе xOy.

а) х²-4у²=20,

b) 3х²+5у²-х-2=0,

c) у²+3х-2=0.

а) 3х²-у²+у-4=20,

b) 5х²+6у²=60,

c) 4х²-х+у =0.

а) -х²+3у²=9,

b) 5х²+4у²-у=0,

c) 3х²+у-2=0.

а) х²+2у²+х-у+7=0,

b) -2х²+7у²=28,

c) 2у²-х+1=0.

а) 2х²+4у²+х=0,

b) -3х²+2у²+2у=5,

c) х²-х-у+2=0.

а) х²-2у²+х-7=0,

b) х²-5у+2=0,

c) х²+2у²+х+у=0.

а) 5х²+9у²-30х-18у=20,

b) 7х²-9у²-2=0,

c) у²-4х=2.

а) 4х²+7у²-8х-у=20,

b) 2х²+2у-х =0,

c) х²+х- у²=0.

а) у²+6х-4=0,

b) 16х²+25у²+32х-10у=284,

c) 2х²-7у²-х=2.

а) х-2у²-2у+1=0,

b) 4х²+3у²-8х+12у-32=0,

c) 5х²-4 у²+2у=0.

а) 3х²-у²+у-4=20,

b) 16х²+9у²-64х+54у-161=0

c) у²-5х+2у=0.

а) х-2у²+12у-14=20,

b) х²+9у²-2х-6у=0,

c) 9х²+90х-16у²+32у=367.

а) у²+х+у=2,

b) 4х²-3у²+4х+1=0,

c) х²-х+ у²+ у=1.

а) 16х²-9у²-64х+-18у=199,

b) 4х²+у²+4х-4=0,

c) х- у²-у=0.

а) 7х²-5у²-14х-20у =22,

b) х+у²-2у+1=0,

c) х²+9у²-6у-2=0.

а) 3х²+2х-у=2,

b) 3х²-2у²-у+1=0,

c) 36х²-36х+36у²-24у-23=0.

а) 2х²-3у²-2у=0,

b) у²+4у-2х+2=0,

c) 4х²+4х+3у²=1.

а) 3х²-у²+7у+10=0,

b) 2х²+3у²-5х=0,

c) х²+6х+5у-6=0.

а) 2х²+х+3у=0,

b) 2х²-у²-у+7=0,

c) 4х²-8х+9у²+36у+4=0.

а) х²-9у²+2х+36у=44,

b) х²+4у²-3х-4у=0,

c) у²+х+2у+1=0.

а) 3х²-у²+2у-3=0,

b) 2х²-8х+3у+19=0,

c) 4х²-4х+у²=0.

а) 4х²-у²+2х=3,

b) -у²+х+2у=60,

c) х²-4х+4у²-8у-8=0.

а) 4х²-8х+7у²-у=20,

b) 5х²-4у²=10,

c) х+у²-4у+2 =0.

а) х²-2х+у=2,

b) х²-3у²+6х+5=0,

c) х²+4х+3у²-2=0.

а) 2х²-у²-8у-9=0,

b) -у²+х-4у+15=0,

c) 4х²+3у²+18у+15=0.

а) 4х²-у²+2х=3,

b) -у²+6х+2у=11,

c) 3х²-2х+2у²=0.

а) 2у²-у+х=0,

b) х²+2у²-3х+1=0,

c) х²-4х-у²-5=0.

а) 4х²-у²-2у=0,

b) 5х²+у²+х-6=0,

c) х²-4х+у =0.

а) 4х²-х-у=5,

b) 2х²+3у²=12,

c) -х²-х+3у²-2=0.

а) 2х²+4у²-1=0,

b) 5х²-3у²+у=0,

c) 3х+у²-2=0.

Задача 6. Определить типы поверхностей по их уравнениям и изобразить поверхности схематически в системе координат Oxyz.

1.	a) x²-3y²+z²=1, b) 3x²+y=0;	2.	a) x²+6y²+24z²=96, b) y²-4z²=4;	3.	a) x²+3y²+4z²=12, b) 4x²- z²+1=0;
4.	a) x²+2y²-2z=0, b) 9x²+4z²=36;	5.	a) x²-y=-9z², b) 8x²+11z²=88;	6.	a) 4x²-8y²+z²+24=0, b) 5x²+y²=5;
7.	a) -x²-4y²+8=z, b) 2x²+3z=0;	8.	a) -5x²-y²+4z²+60=0, b) 7x²+5y²=35;	9.	a) 4x²-5y²-5z²+40=0, b) z²-4x+8=0;
10.	a) 7x²-3y²-z²=21, b) 5y²+8z²=40;	11.	a) -16x²+y²+4z²=32, b) 3y²+4z²=10;	12.	a) x²-8y²-8z²=0, b) 5x²-6z²=30;
13.	a) 2x²+3y²-z²=18, b) 3y²+z²=6;	14.	a) 4x²-6y²+3z²=0, b) 3x²-8y²=228;	15.	a) x²+4z²=2y, b) 2y²-5z²=10;
16.	a) 6x²-y²+3z²=12, b) 2x²+6y²=12;	17.	a) 3x²+12y²+4z²=48, b) 3x²+5z=15;	18.	a) 6x²+y²+6z²=18, b) x²= -3z;
19.	a) -3x²+6y²-z²=18, b) x²-9y²=9;	20.	a) 2x²+3y²-z²=36, b) 6y²+5z²=30;	21.	a) 4x²-y²-6z²=-1, b) 3y²+z²=6;
22.	a) -x²-y²-z+4=0, b) 2x²+3z²=6;	23.	a) 3x²-y+4z²=0, b) 3x²+4z²=24;	24.	a) 9x²+6y²-6z²+16=0 b) y²+5z²=15;
25.	a) 10x²+6y²-15z=0, b) 5x²-7z²+35=0;	26.	a) 4x²+6y²+24z²=96, b) y²-4z²=4;	27.	a) 4x²+3y²=-12z, b) 3x²+6x+z=0;
28.	a) 3x²-4y²-2z²=-12, b) y²-2y+z=0;	29.	a) x²-y=-9z², b) 8x²+11z²=88;	30.	a) 2x²-3y²-5z²=30, b) y²=4z-2.

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в предмете Математика

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18.
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.