
- •Программа курса математики
- •Тема I. Векторная алгебра и аналитическая геометрия
- •Тема II. Дифференциальное исчисление
- •Основные понятия, формулы, правила Вычисление определителей
- •Системы линейных алгебраических уравнений
- •Векторная алгебра
- •Прямая на плоскости
- •Кривые второго порядка
- •Аналитическая геометрия в пространстве
- •Канонические уравнения поверхностей 2-го порядка
- •Дифференциальное исчисление
- •Задания к типовому расчету №1 Системы линейных уравнений. Аналитическая геометрия
- •Математический анализ
- •Примеры решения задач из типового расчета
- •Библиографический список
- •Оглавление
- •394006 Воронеж, ул. 20-летия Октября, 84
Прямая на плоскости
Составить уравнение
прямой
![]() на плоскости возможно:
на плоскости возможно:
если известны две точки
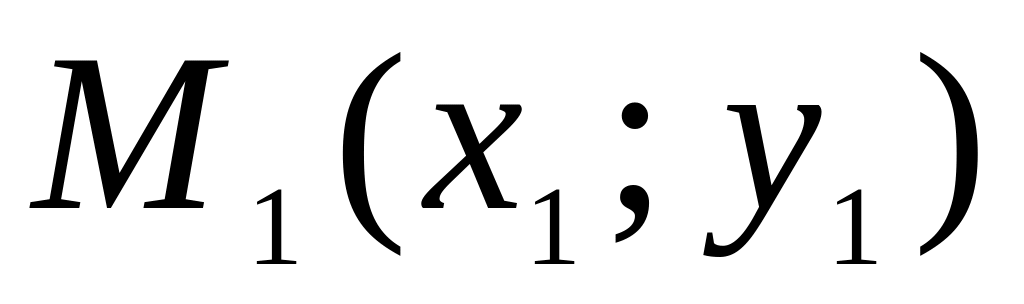 и
и
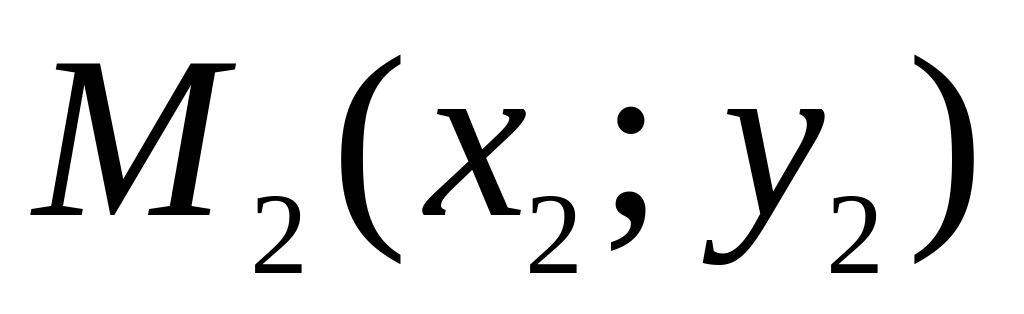 ,
лежащие на прямой
:
,
лежащие на прямой
:
![]() ;
;
если известна точка , лежащая на прямой, и прямая параллельна вектору
 :
:
 (
( -
направляющий вектор прямой);
-
направляющий вектор прямой);если известна точка
 ,
лежащая на прямой, и прямая перпендикулярна
нормальному вектору
,
лежащая на прямой, и прямая перпендикулярна
нормальному вектору
 :
:
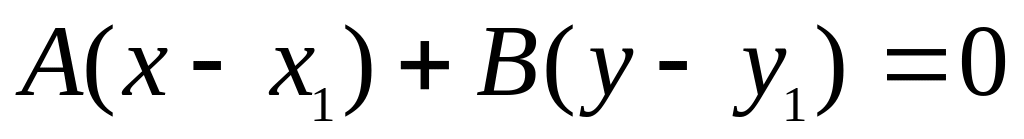 или
или
 (общее уравнение прямой);
(общее уравнение прямой);если известен угловой коэффициент прямой
 ,
где
– угол образуемый прямой с осью Ox:
,
где
– угол образуемый прямой с осью Ox:
 (уравнение
прямой с угловым коэффициентом).
(уравнение
прямой с угловым коэффициентом).
Угол
между прямыми (![]() )
)
![]() и (
и (![]() )
)
![]() определяется формулой
определяется формулой
![]() ,
где плюс соответствует острому углу, а
минус тупому. Отсюда:
,
где плюс соответствует острому углу, а
минус тупому. Отсюда:
![]() – условие параллельности прямых (
– условие параллельности прямых (![]() );
условие перпендикулярности прямых при
);
условие перпендикулярности прямых при
![]() имеет вид
имеет вид
![]() .
.
Расстояние от
точки
![]() до прямой
,
заданной уравнением
,
определяется по формуле
до прямой
,
заданной уравнением
,
определяется по формуле
![]() .
.
Кривые второго порядка
Кривыми второго порядка являются окружность, эллипс, гипербола, парабола, общее уравнение которых имеет вид
![]() .
.
Э ллипс
– это множество точек плоскости, сумма
расстояний от которых до двух фиксированных
точек
ллипс
– это множество точек плоскости, сумма
расстояний от которых до двух фиксированных
точек
![]() и
и
![]() (называемых фокусами), есть величина
постоянная:
(называемых фокусами), есть величина
постоянная:
![]() .
.
К
Рис.2. Эллипс![]() (см. рис. 2), где
(см. рис. 2), где
![]() -
полуоси эллипса, зная которые можно
определить координаты фокусов
-
полуоси эллипса, зная которые можно
определить координаты фокусов
![]() и
и
![]() ,
где
,
где
![]() .
Если
.
Если
![]() ,
то получается уравнение окружности
,
то получается уравнение окружности
![]() с центром в начале координат и радиусом
с центром в начале координат и радиусом
![]() .
.
Г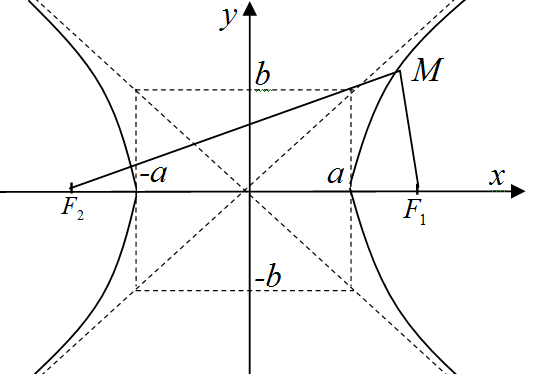 ипербола
– это множество точек
плоскости, модуль разности расстояний
от которых до двух фиксированных точек
ипербола
– это множество точек
плоскости, модуль разности расстояний
от которых до двух фиксированных точек
![]() и
и
![]() (называемых фокусами), есть величина
постоянная:
(называемых фокусами), есть величина
постоянная:
![]() .
.
К
Рис.3. Гипербола![]() (см. рис. 3), где
(см. рис. 3), где
![]() -
действительная и мнимая полуоси кривой,
зная которые можно определить
координаты фокусов
-
действительная и мнимая полуоси кривой,
зная которые можно определить
координаты фокусов
![]() ,
где
,
где
![]() .
Уравнение
.
Уравнение
![]() определяет гиперболу, у которой
определяет гиперболу, у которой
![]() -
действительная и мнимая полуоси, а
фокусы находятся в точках
-
действительная и мнимая полуоси, а
фокусы находятся в точках
![]() .
.
Прямые
![]() называются асимптотами гиперболы, к
ним приближаются ветви гиперболы при
называются асимптотами гиперболы, к
ним приближаются ветви гиперболы при
![]() .
Указанные асимптоты проходят по
диагоналям прямоугольника (см. рис. 3).
.
Указанные асимптоты проходят по
диагоналям прямоугольника (см. рис. 3).
П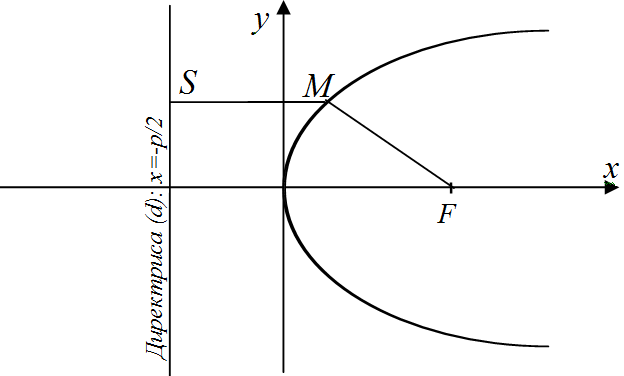 арабола
– это множество точек плоскости,
равноудаленных от фиксированной
точки
арабола
– это множество точек плоскости,
равноудаленных от фиксированной
точки
![]() (фокуса) и от прямой
(фокуса) и от прямой
![]() (директрисы):
(директрисы):
![]() ,
расстояние от фокуса до директрисы
равно
,
расстояние от фокуса до директрисы
равно
![]() .
.
Е
Рис.4. Парабола
![]() (см. рис. 4), где
- параметр параболы, зная который можно
определить коорди-наты фокуса
(см. рис. 4), где
- параметр параболы, зная который можно
определить коорди-наты фокуса
![]() и уравнение директрисы
и уравнение директрисы
![]() .
.
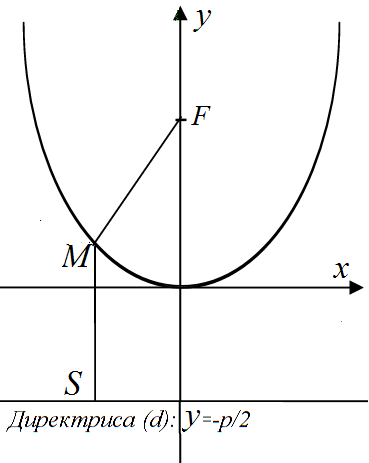
Е
Рис.5. Парабола![]() (см. рис. 5). Тогда координаты фокуса
(см. рис. 5). Тогда координаты фокуса
![]() и уравнение директрисы
и уравнение директрисы
![]() .
.
Аналитическая геометрия в пространстве
Составить уравнение плоскости возможно:
если известны три точки
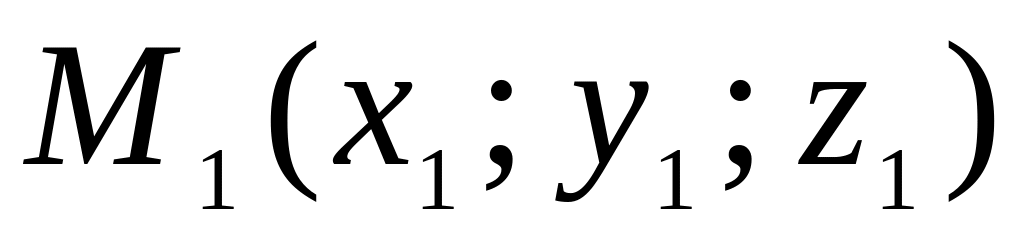 ,
,
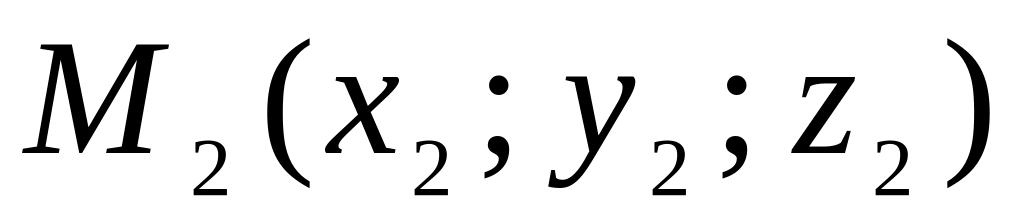 и
и
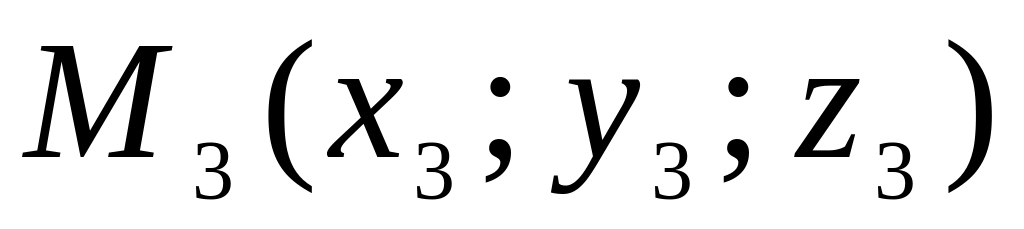 ,
которые принадлежат плоскости, но не
лежат на одной прямой:
,
которые принадлежат плоскости, но не
лежат на одной прямой:
 ;
;
если известен нормальный вектор
 плоскости и координаты точки
плоскости и координаты точки
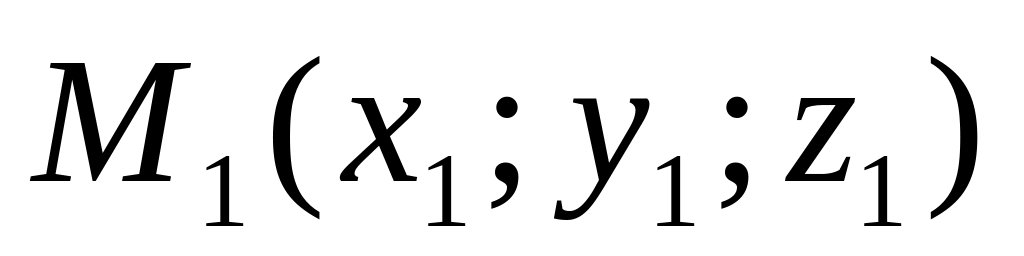 ,
принадлежащей плоскости:
,
принадлежащей плоскости:
 .
.
Раскрыв скобки в
последнем уравнении, получим общее
уравнение плоскости:
![]() .
.
Составить уравнения прямой возможно:
если известны две точки и , принадлежащие прямой:
 ;
;
если известны направляющий вектор прямой
 и координаты точки
,
принадлежащей прямой:
и координаты точки
,
принадлежащей прямой:
 .
.
Угол между
плоскостями
![]() и
и
![]()
равен углу между
их векторами нормали
![]() ,
,
![]() :
:
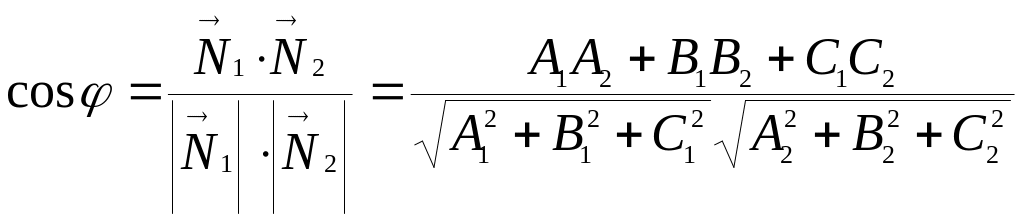 .
.
Угол между прямыми
![]() и
и
![]() равен углу между их направляющими
векторами
равен углу между их направляющими
векторами
![]() ,
,
![]() :
:
 .
.
Угол
![]() между плоскостью
между плоскостью
![]() и прямой
и прямой
![]() определяется формулой
определяется формулой
![]() .
.
Расстояние от
точки
до плоскости
определяется по формуле:
![]() .
.
