Вариант №6

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать матрицу поворота вокруг оси ОY на угол по часовой стрелке.

№5. .

№6. .

№7. .

№8. , .

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать на плоскости матрицу симметрии относительно оси ОX.

№5. .

№6. .

№7. .

№8. , .

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать матрицу линейного преобразования, при котором по оси ОZ происходит растяжение в 7 раз, а по оси ОX сжатие в 2 раза. Преобразование симметрично относительно плоскости YОZ.

№5. .

№6. .

№7. .

№8. ,

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2 .

№3. , .

№4. Написать матрицу поворота вокруг оси ОZ на угол против часовой стрелки.

№5. .

№6. .

№7. .

№8. ,

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать на плоскости матрицу симметрии относительно биссектрисы второго и четвертого координатных углов.

№5. .

№6. .

№7. .

№8. , .

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать матрицу линейного преобразования, при котором по оси ОX происходит растяжение в 3 раза, а по оси ОY сжатие в 5 раз. Преобразование на оси ОZ точки оставляет на месте.

№5. .

№6.

.

№7. .

№8. , .

№9. .

№10.

№11.

№12.

№1. , .

Найти матрицу из уравнения .

№2. .

№3. , .

№4. Написать матрицу поворота вокруг оси ОX на угол по часовой стрелке.

№5. .

№6. .

№7. .

№8. , .

№9. .

№10.

№11.

№12.
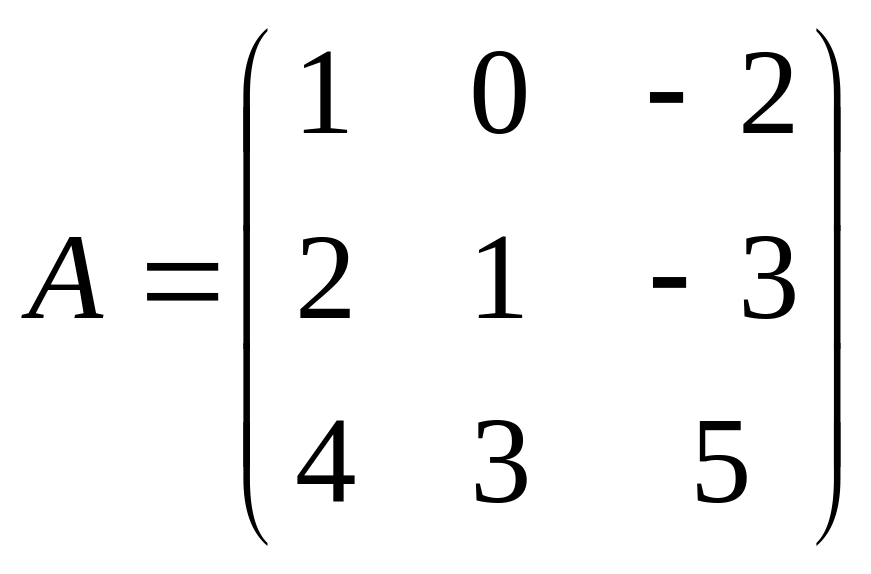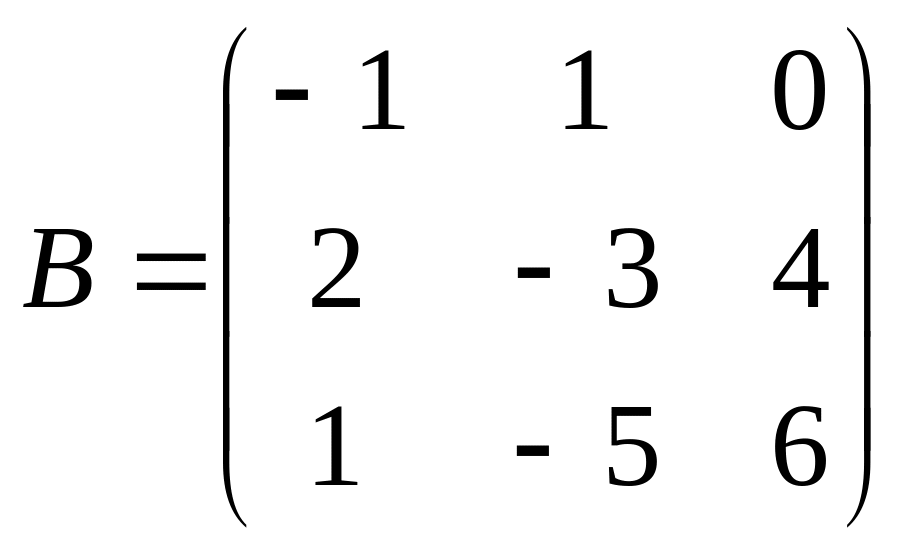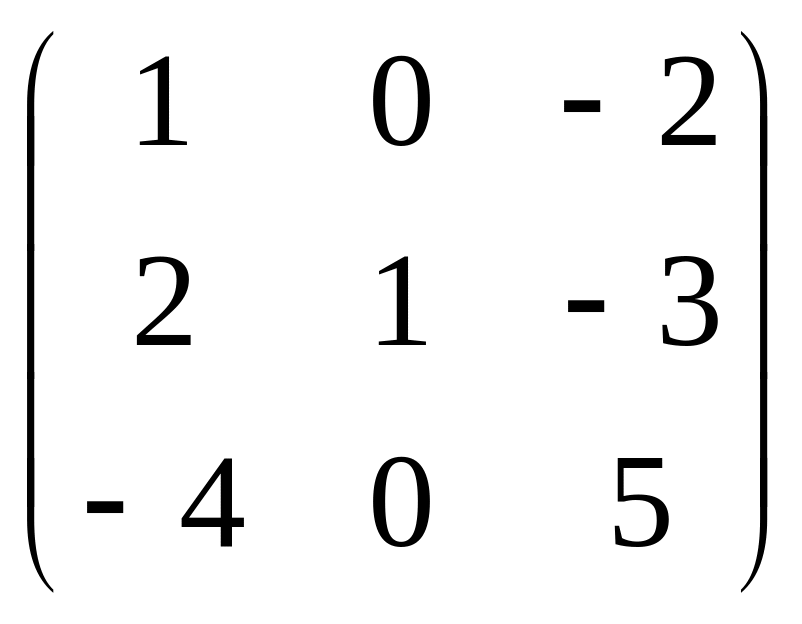
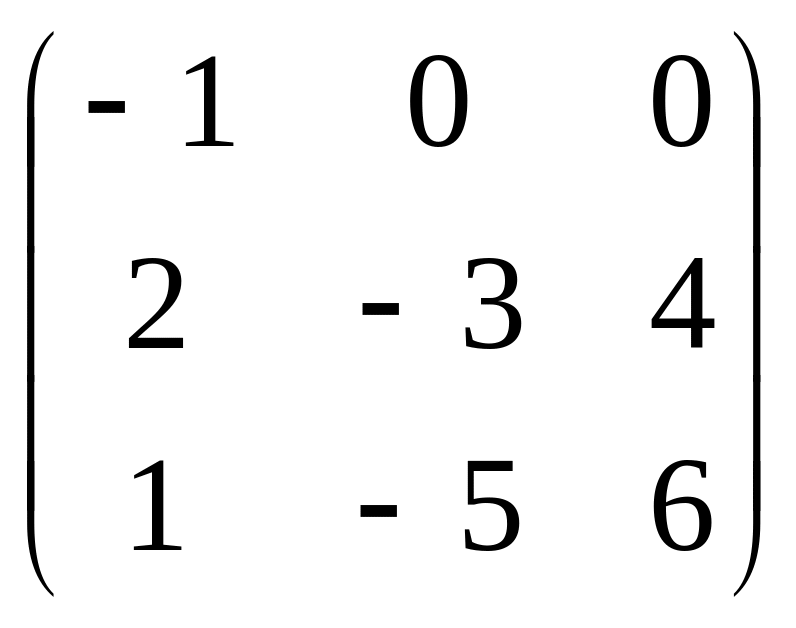
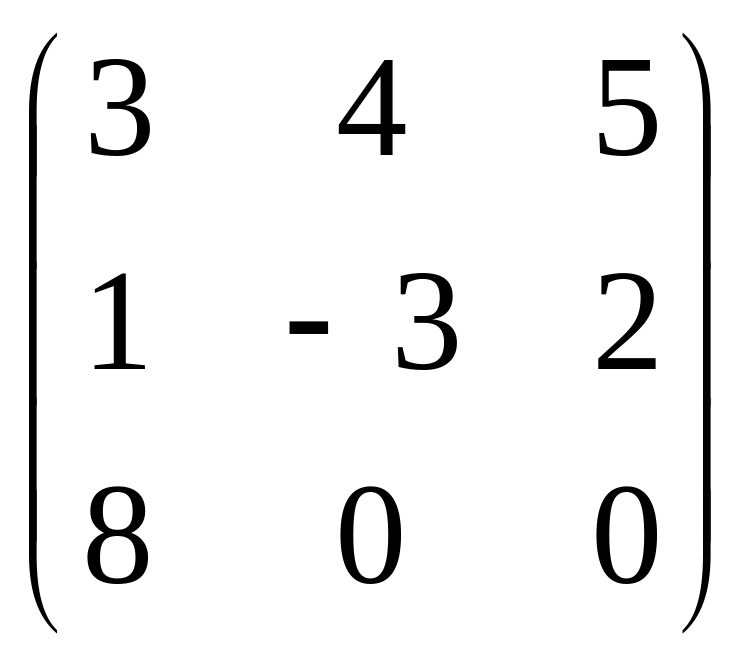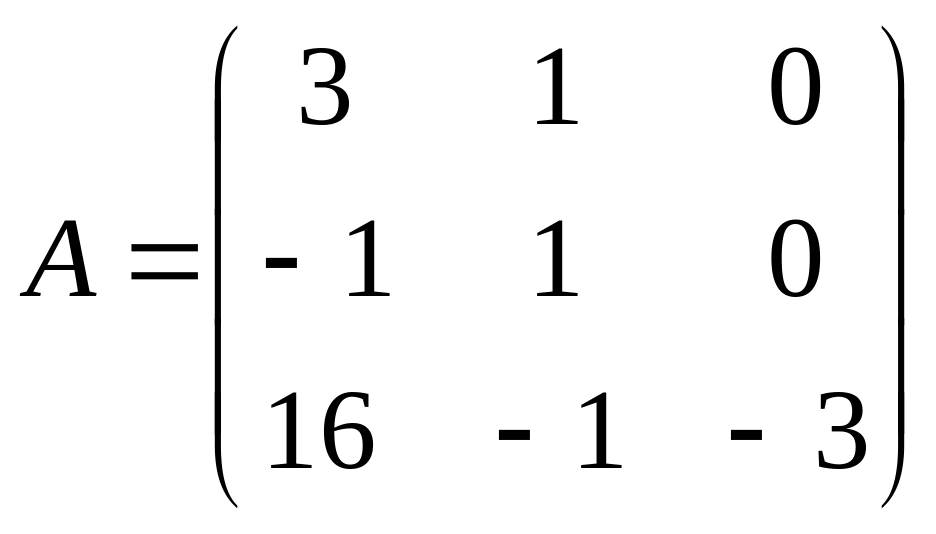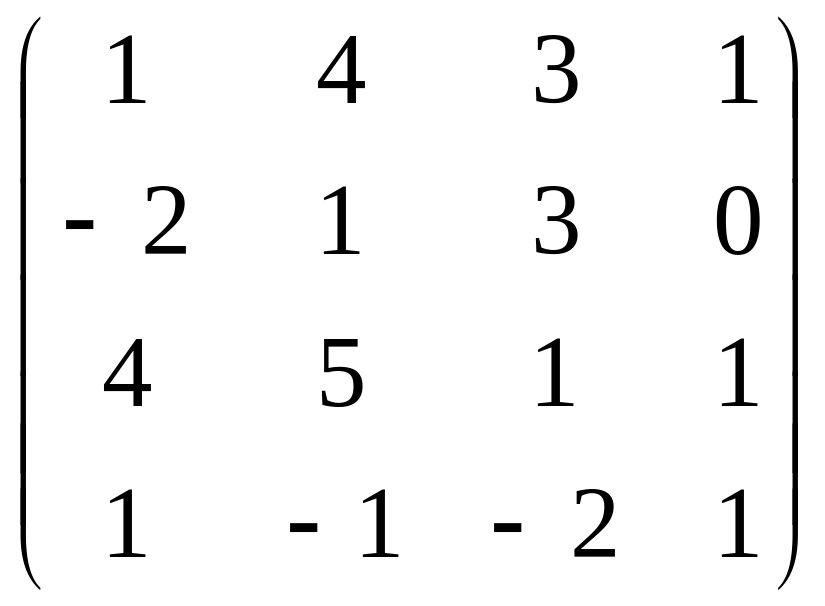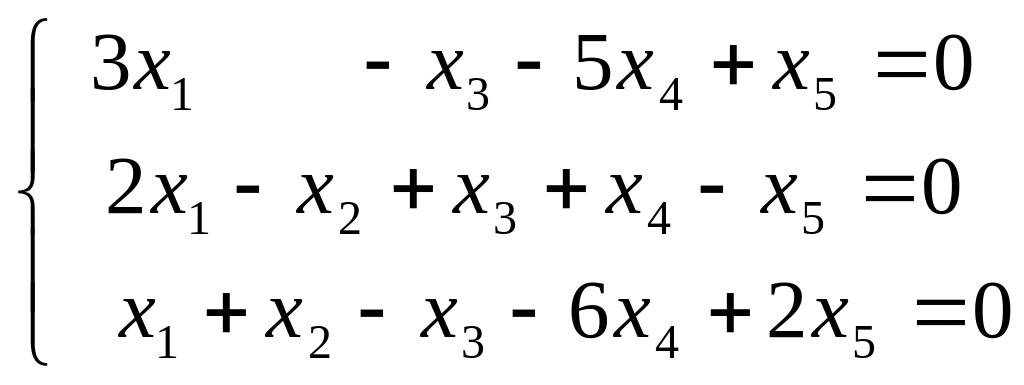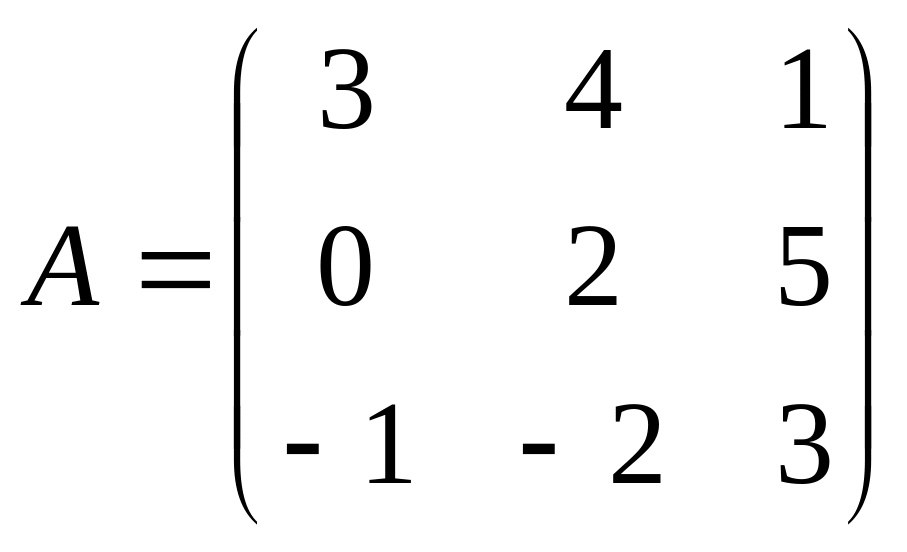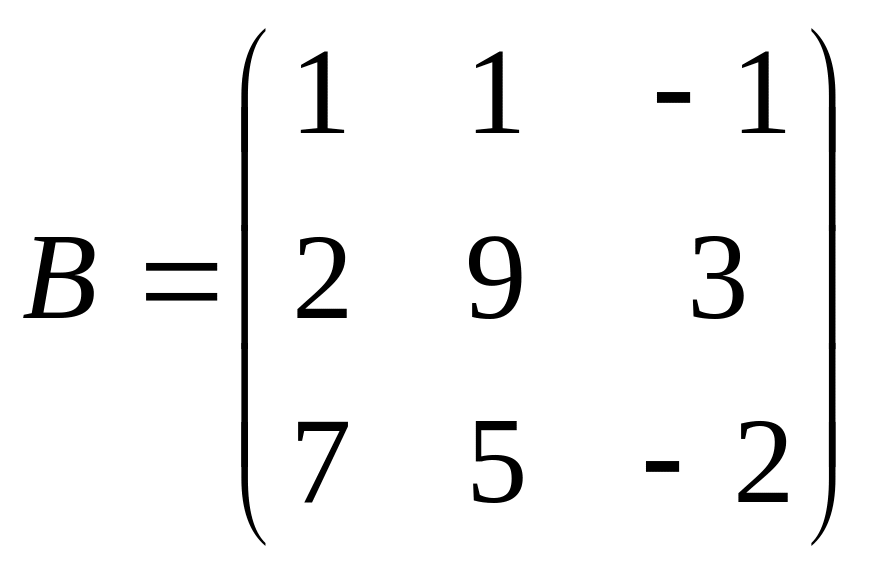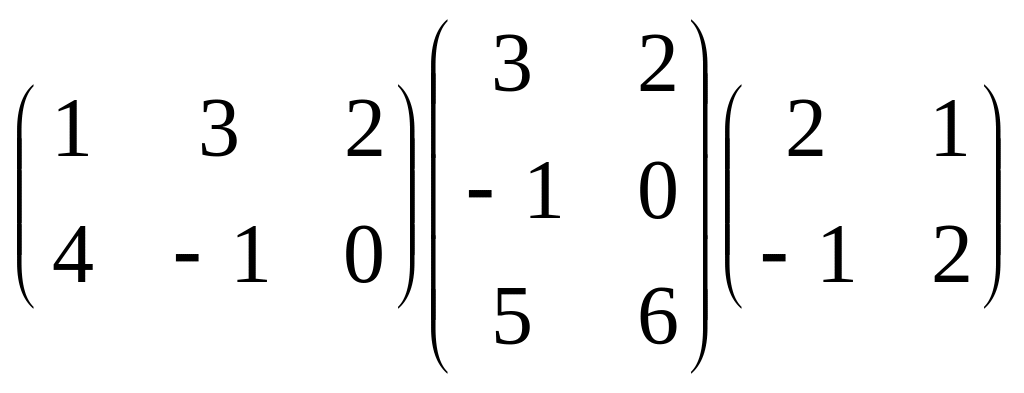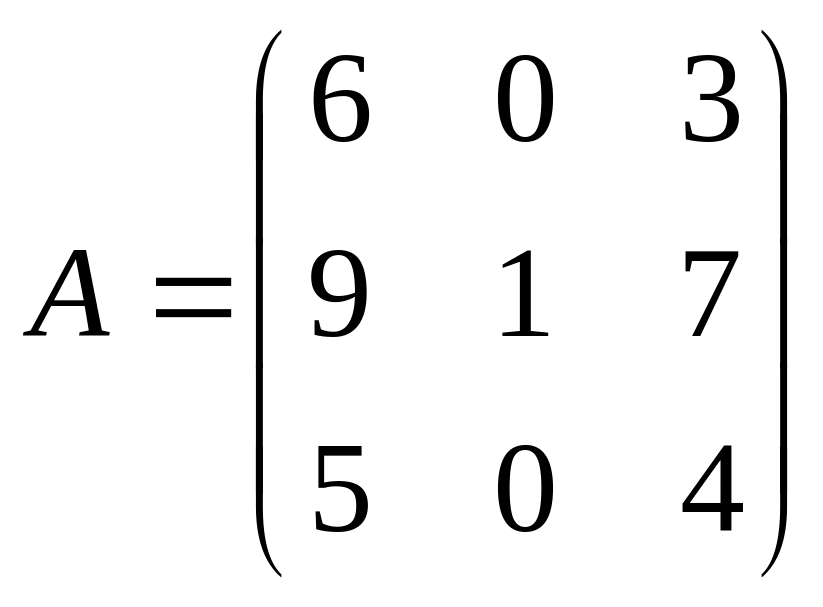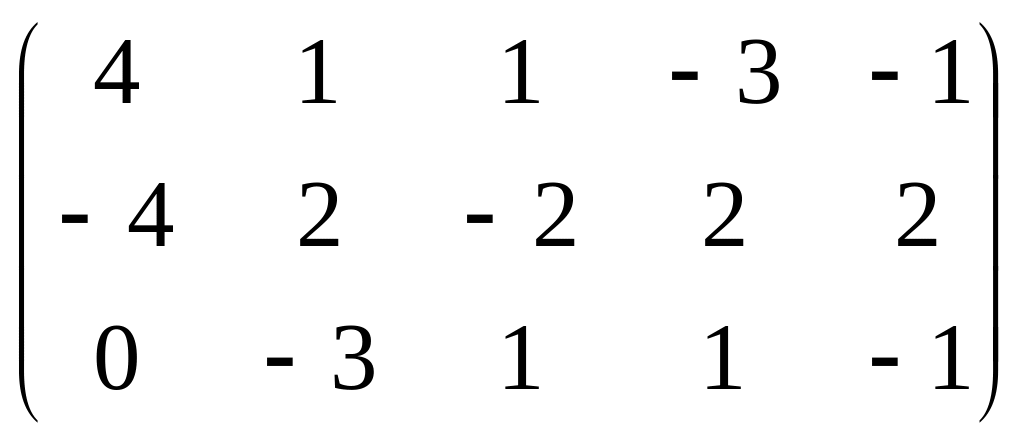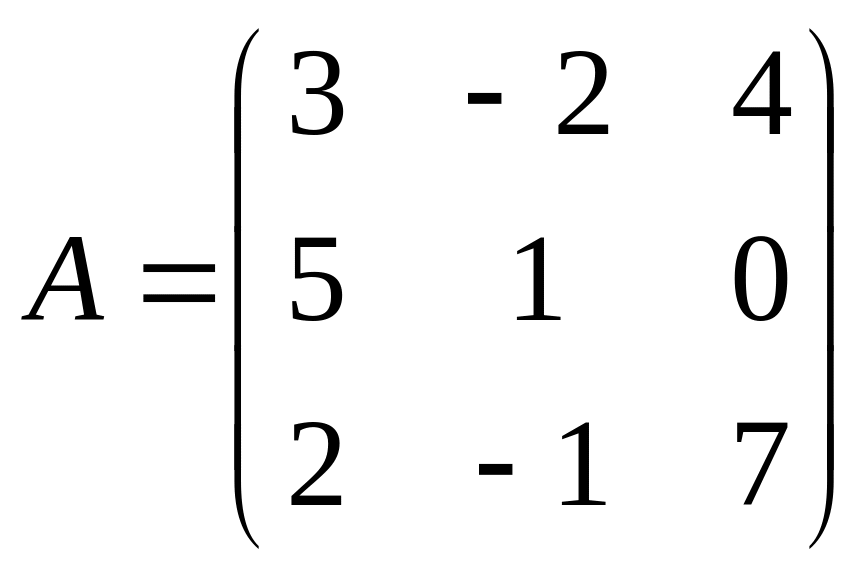
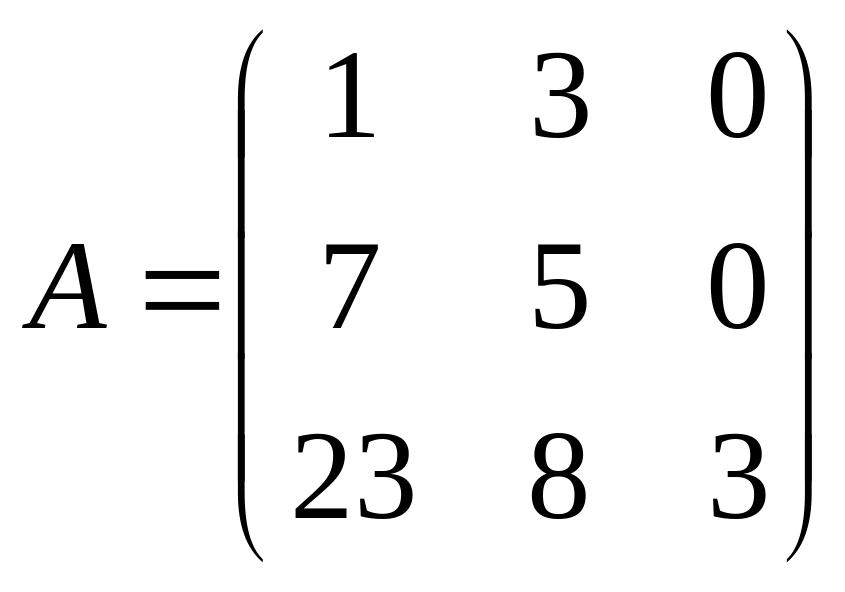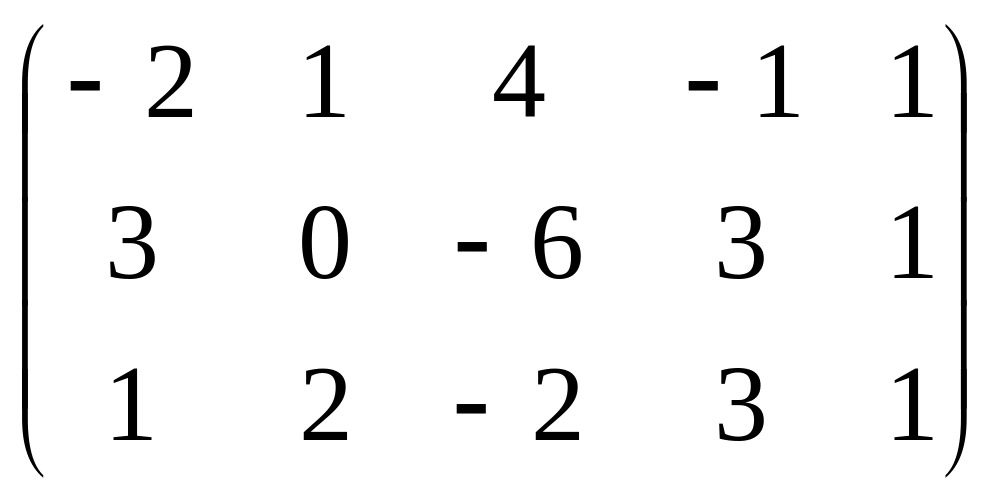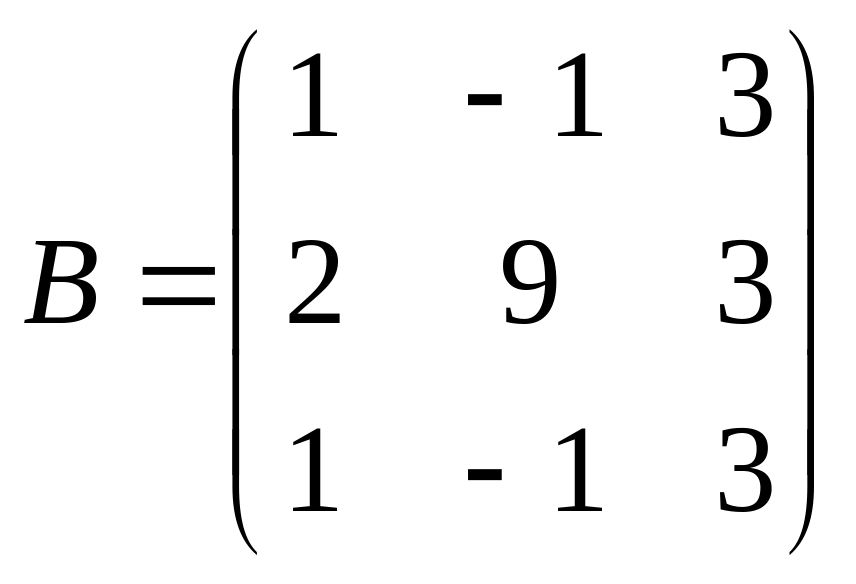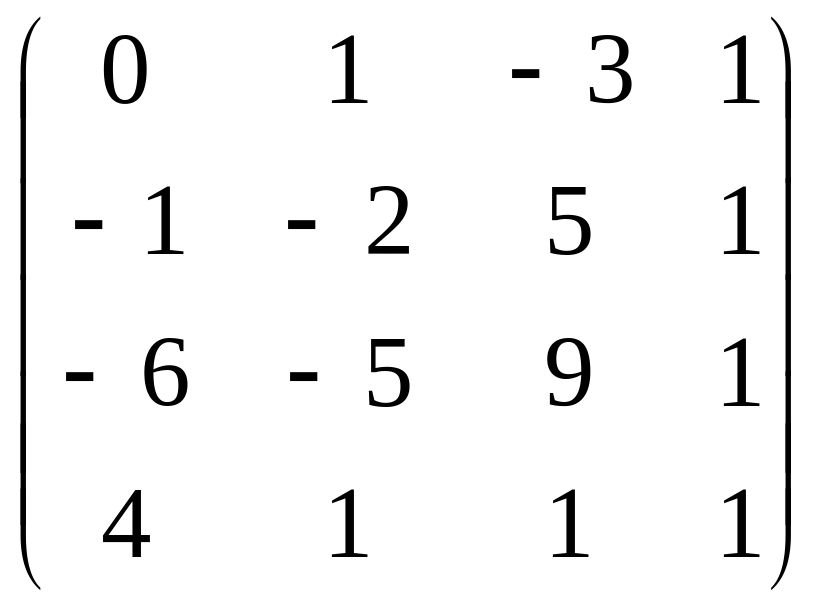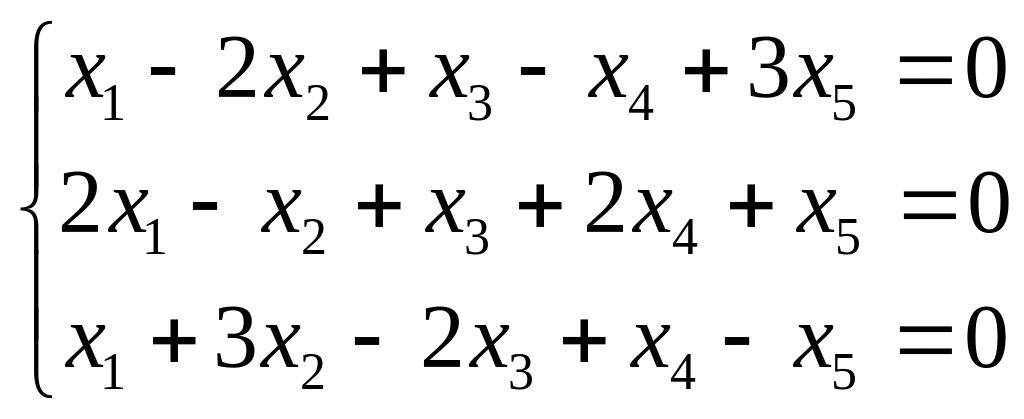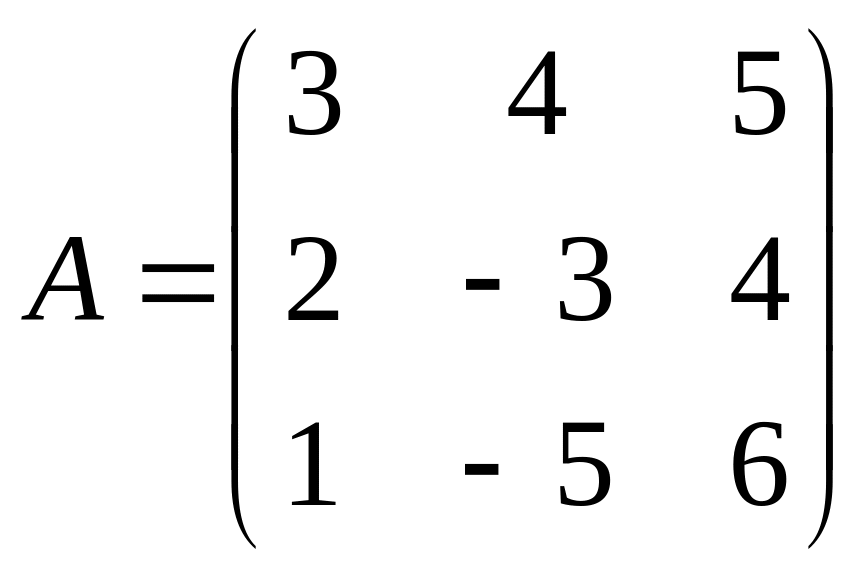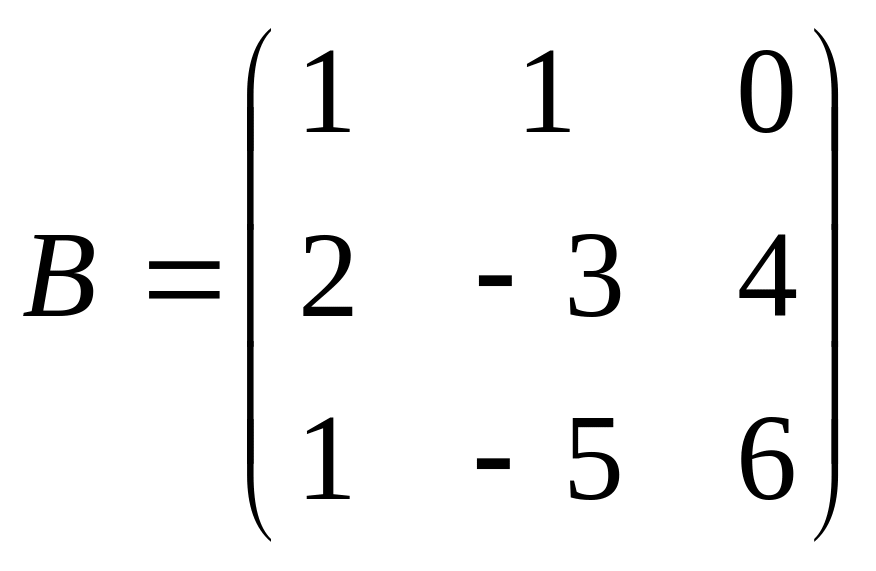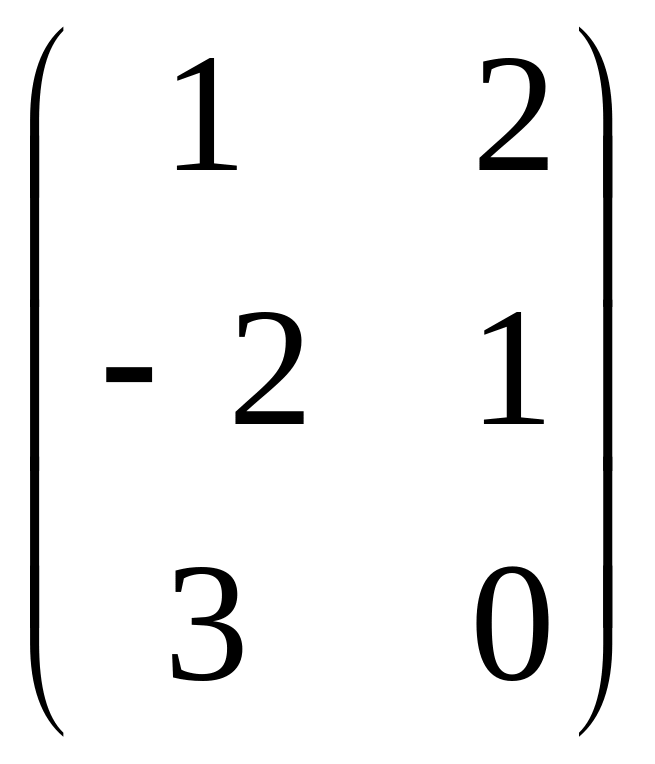
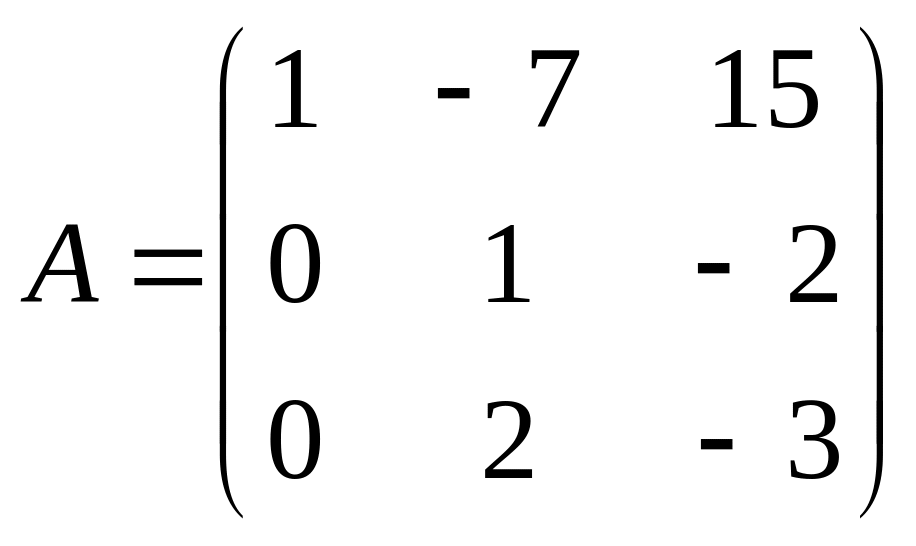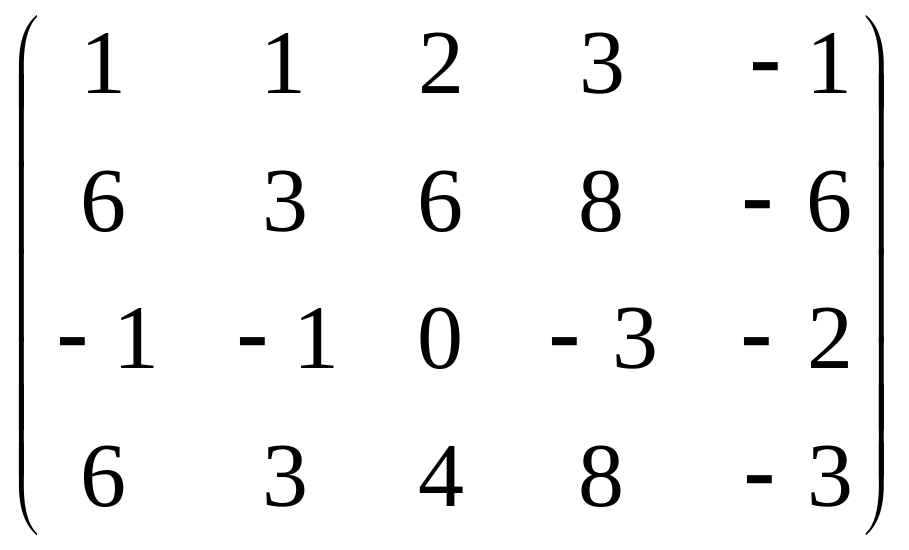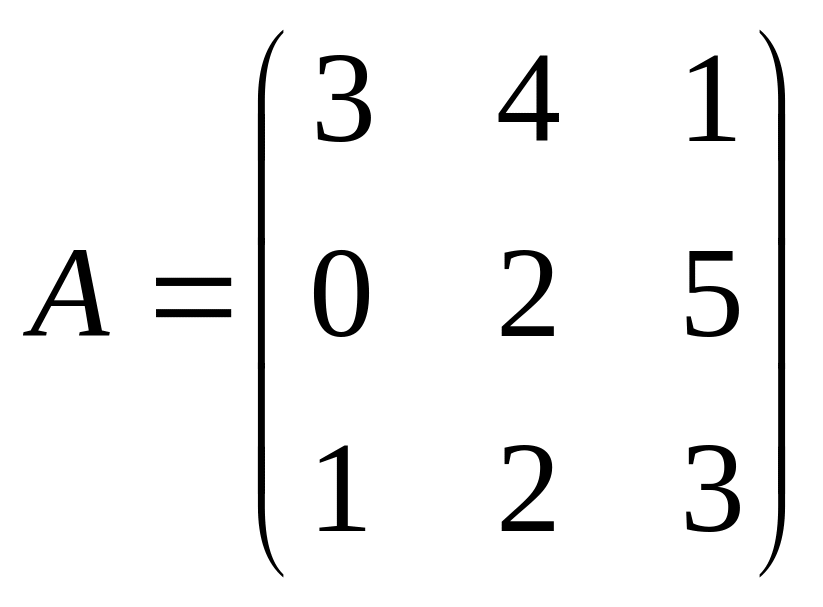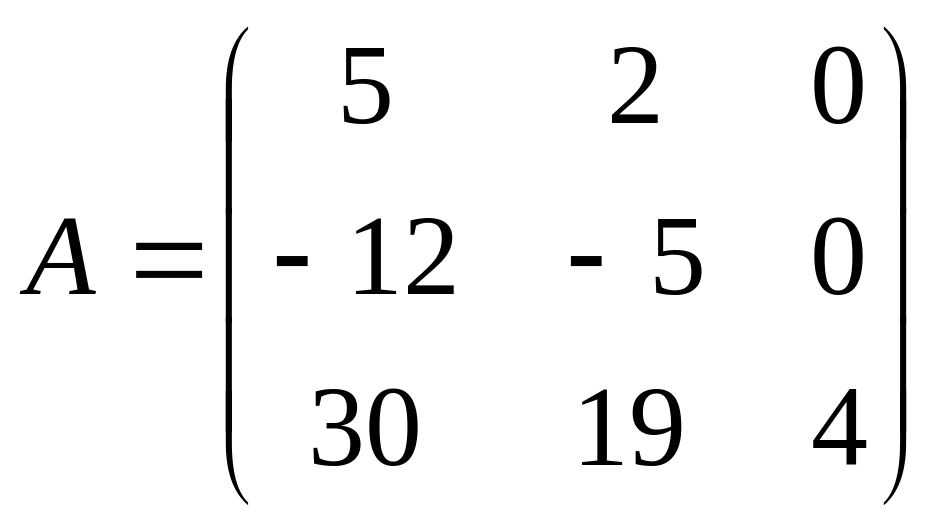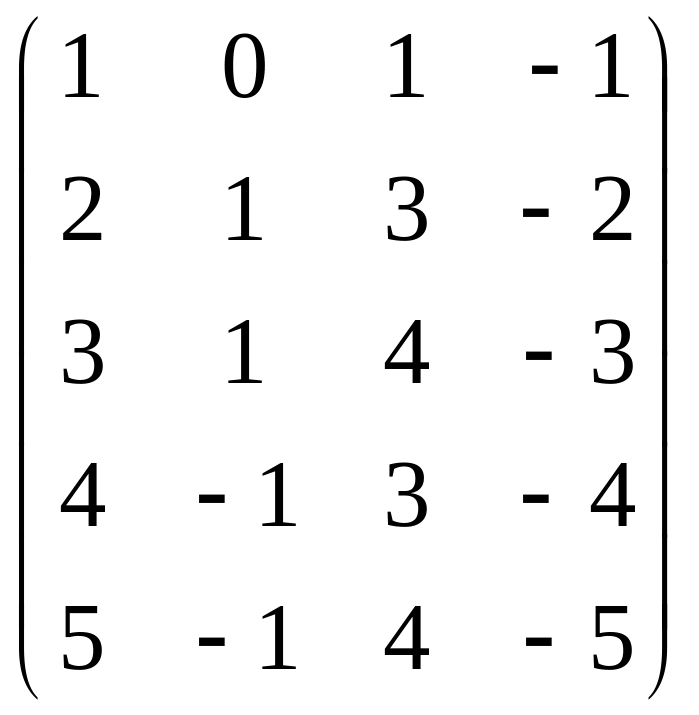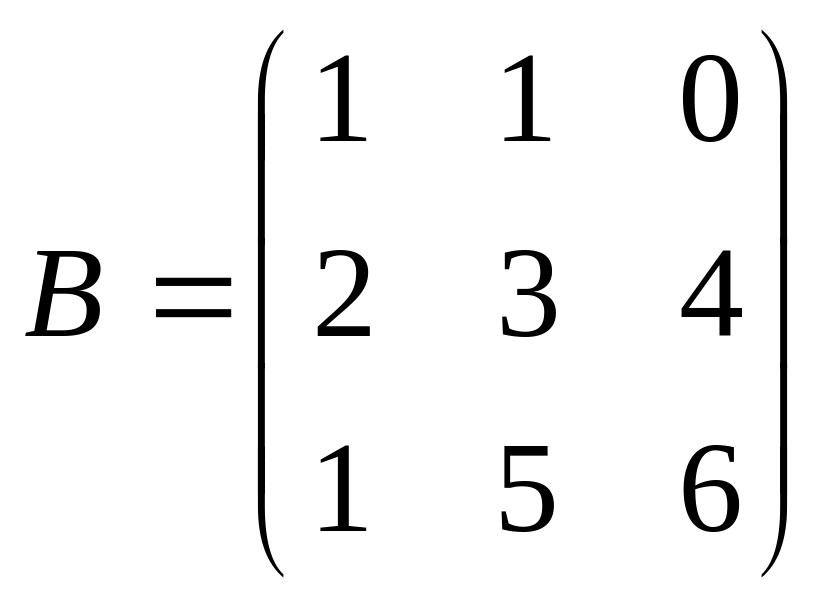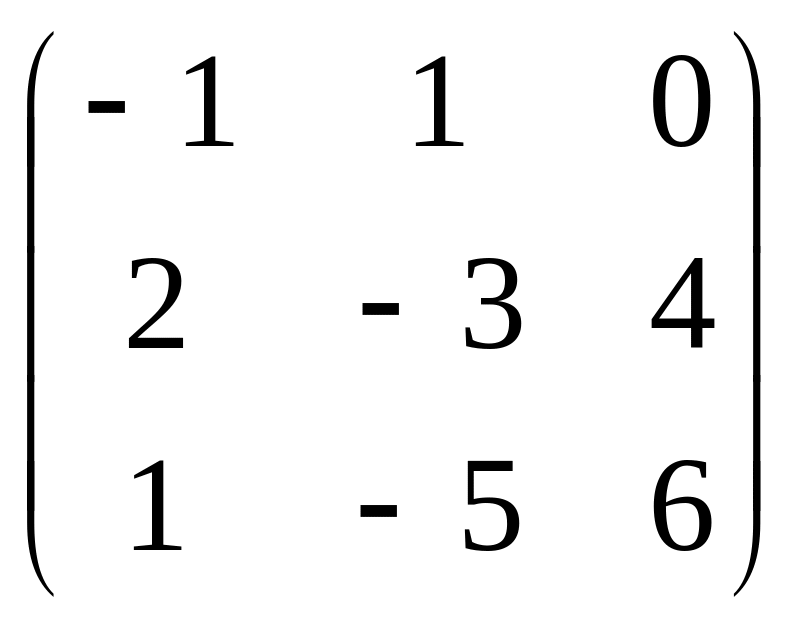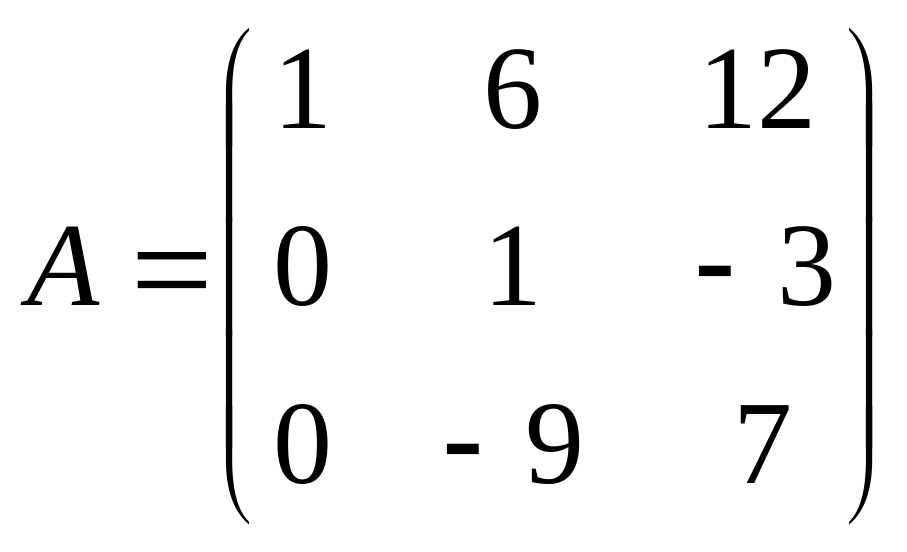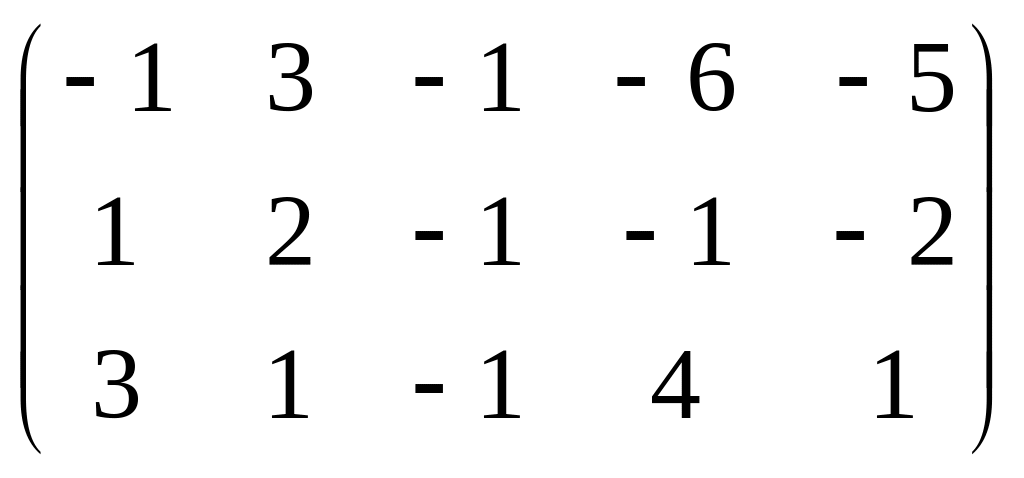