
- •Линейная алгебра
- •Введение
- •1. Операции над матрицами
- •2. Линейные преобразования и матрицы
- •Обратная матрица. Решение систем линейных уравнений матричным способом
- •Ранг матрицы. Решение систем линейных уравнений
- •Собственные числа и собственные векторы квадратной матрицы
- •Приведение квадратичной формы к каноническому виду
- •Решение однородных систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Характеристика задания
- •Варианты контрольных заданий
- •Вариант № 5
- •Вариант №6
- •Вариант № 7
- •Вариант № 8
- •Вариант №9
- •Вариант № 10
- •Вариант № 11
- •Вариант №12
- •Вариант № 13
- •Вариант № 14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Библиографический список
- •Оглавление
- •Линейная алгебра
- •394006 Воронеж, ул. 20-летия Октября, 84
Собственные числа и собственные векторы квадратной матрицы
Рассмотрим квадратную матрицу n
-го порядка
![]() ,
,
![]() и n-мерный вектор
и n-мерный вектор
![]() .
.
Если линейное преобразование (задаваемое
матрицей
)
ненулевого вектора
![]() ,
тождественно операции умножения вектора
на некоторый скаляр
,
тождественно операции умножения вектора
на некоторый скаляр
![]() ,
т.е.
,
т.е.
![]() (
(![]() ), (23)
), (23)
то скаляр называется собственным значением указанной матрицы, а вектор , соответствующий собственному значению , есть собственный вектор матрицы .
Для определения собственных значений запишем (23) в виде
![]() , (24)
, (24)
что дает однородную систему
![]() . (25)
. (25)
Для того чтобы однородная система (25) имела отличное от нуля решение и, следовательно, матрица имела хотя бы один отличный от нуля собственный вектор, необходимо, чтобы её основной определитель был равен нулю
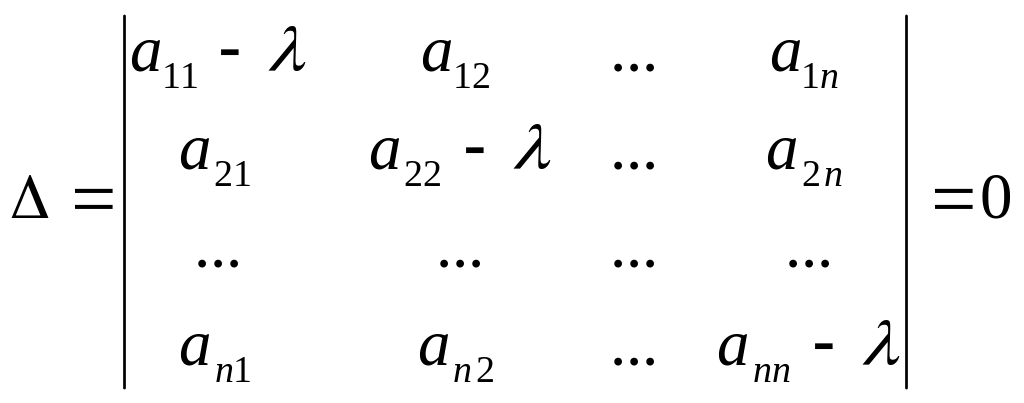 (т.е.
(т.е.
![]() ). (26)
). (26)
Этот определитель называется
характеристическим определителем
матрицы
,
а уравнение
![]() именуется характеристическим (вековым)
уравнением той же матрицы. Определитель
именуется характеристическим (вековым)
уравнением той же матрицы. Определитель
![]() представляет собой многочлен
-ой
степени относительно
.
представляет собой многочлен
-ой
степени относительно
.
Решив характеристическое уравнение
(26), находим собственные значения
![]() ,
среди которых могут быть кратные корни.
Далее для разных собственных чисел
,
среди которых могут быть кратные корни.
Далее для разных собственных чисел
![]() (с учетом кратности) составляются
однородные системы (25)
(с учетом кратности) составляются
однородные системы (25)
![]() ,
,
![]() (с нулевым определителем и бесчисленным
множеством ненулевых решений), решая
которые находят решения – соответствующие
собственные векторы.
(с нулевым определителем и бесчисленным
множеством ненулевых решений), решая
которые находят решения – соответствующие
собственные векторы.
Укажем некоторые основные свойства собственных значений и собственных векторов:
Собственный вектор матрицы определяется с точностью до постоянного множителя (если
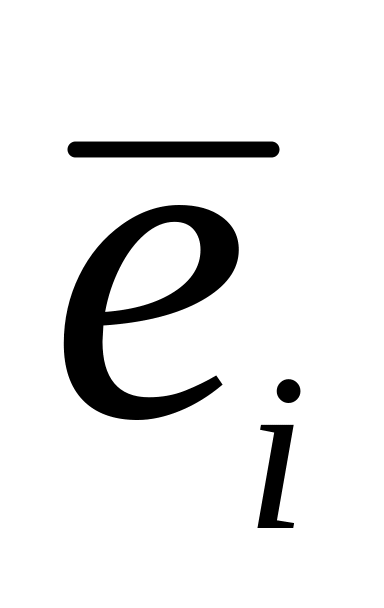 собственный вектор собственного
значения
собственный вектор собственного
значения
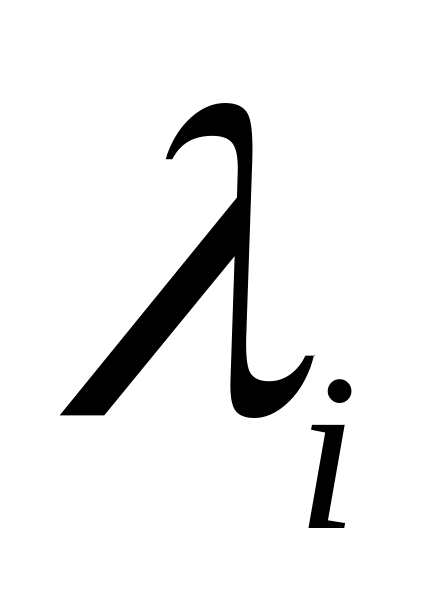 для всех
,
то
для всех
,
то
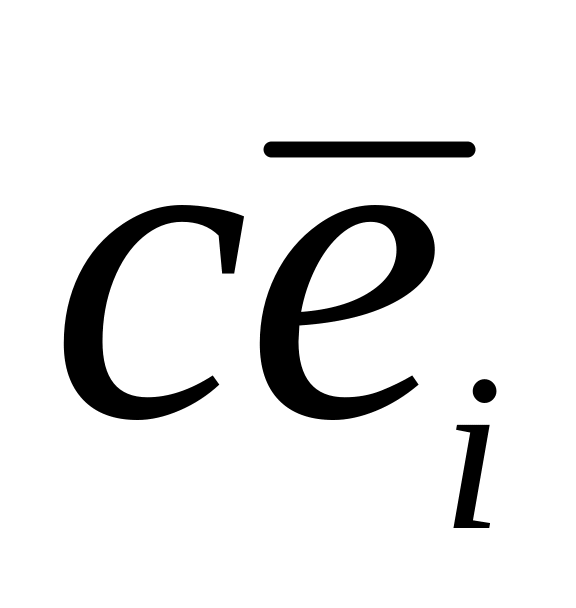 тоже собственный вектор с тем же
собственным значением).
тоже собственный вектор с тем же
собственным значением).Собственный вектор имеет единственное собственное значение (обратное утверждение не верно, у одного собственного значения может быть несколько собственных векторов).
Собственные векторы матрицы, принадлежащие различным собственным значениям, линейно независимы.
Симметрическая матрица (транспонирование которой ее не меняет) имеет только действительные собственные значения.
Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны.
Пример 14. Найти собственные значения
и собственные векторы квадратной матрицы
![]() .
.
Решение. Решать будем пошагово.
1) Выпишем характеристическое уравнение матрицы.
![]() .
.
У полученного квадратного уравнения
корни
![]() ,
,
![]() являются собственными значениями
матрицы
.
являются собственными значениями
матрицы
.
2) Собственные векторы определяются из
системы (25)
![]() .
.
Для собственного значения
получим систему![]() ,
которая эквивалентна одному уравнению
с двумя неизвестными
,
которая эквивалентна одному уравнению
с двумя неизвестными
![]() .
Положив
.
Положив
![]() ,
найдем из уравнения
,
найдем из уравнения
![]() ,
что дает собственный вектор
,
что дает собственный вектор
![]() .
.
Для собственного значения
![]() получим систему
получим систему![]() ,
которая эквивалентна одному уравнению
с двумя неизвестными
,
которая эквивалентна одному уравнению
с двумя неизвестными
![]() .
Положив
,
найдем из уравнения
.
Положив
,
найдем из уравнения
![]() ,
что дает собственный вектор
,
что дает собственный вектор
![]() .
.
Ответ: собственным значениям
![]() и
и
![]() соответствуют собственные векторы
соответствуют собственные векторы
![]() и
и
![]() .
.
Замечание. Для матрицы второго порядка у системы уравнений (26) для нахождения собственных векторов эти уравнения будут пропорциональными.
Пример 15. Найти собственные значения и собственные векторы соответствующие симметрической квадратной матрице третьего порядка
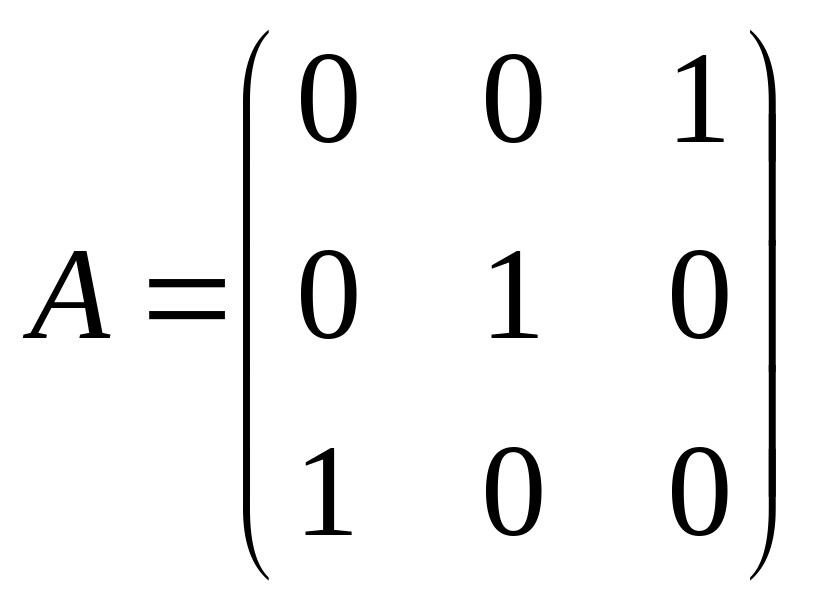 .
.
Решение. 1) Характеристическое уравнение матрицы имеет вид:
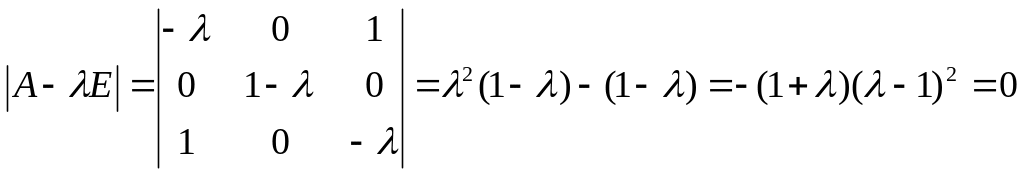 .
.
Его корни
![]() (простой),
(простой),
![]() (двукратный) являются собственными
значениями матрицы
.
(двукратный) являются собственными
значениями матрицы
.
2) Найдем собственные векторы, соответствующие собственным значениям.
Для собственного значения
![]() получим систему
получим систему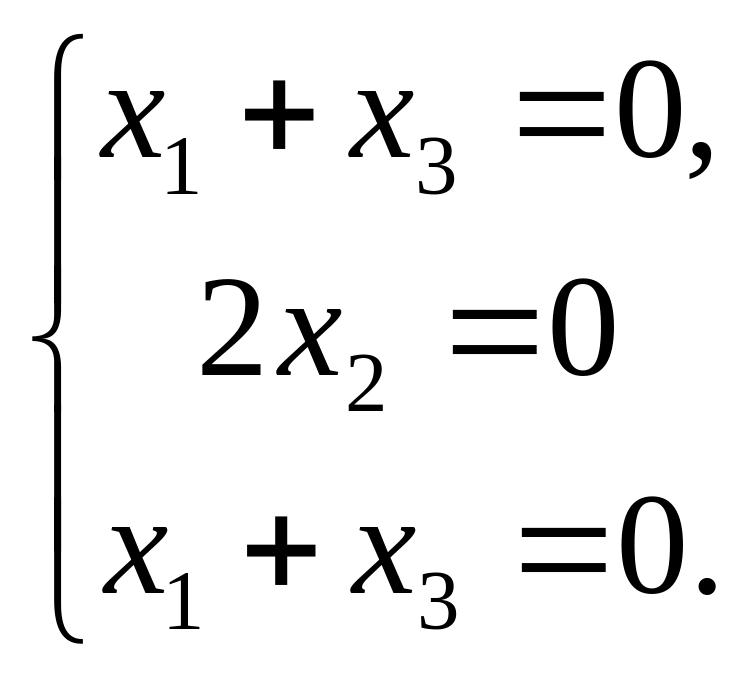 ,
которая эквивалентна двум уравнениям
,
которая эквивалентна двум уравнениям
![]() .
Очевидно, переменная
.
Очевидно, переменная
![]() .
Положив
,
найдем из первого уравнения
.
Положив
,
найдем из первого уравнения
![]() ,
что дает собственный вектор
,
что дает собственный вектор
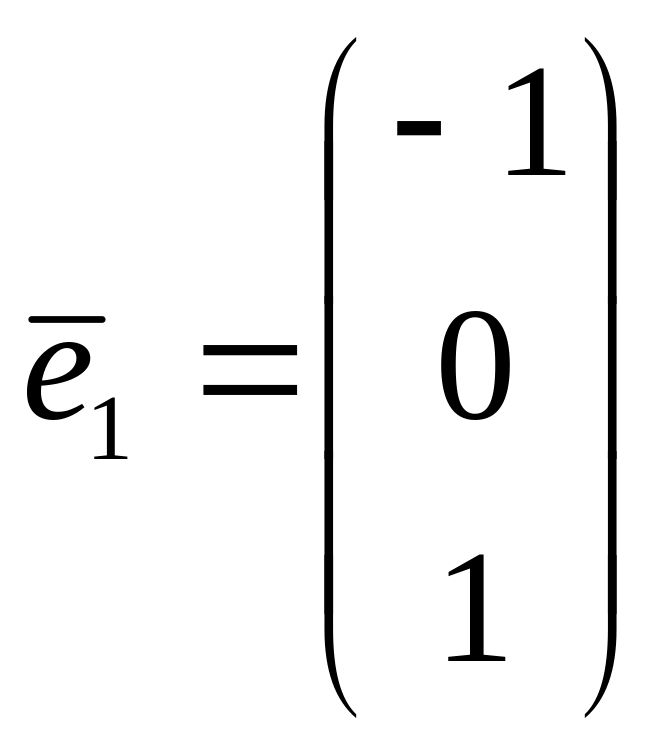 .
.
Для собственного значения
получим систему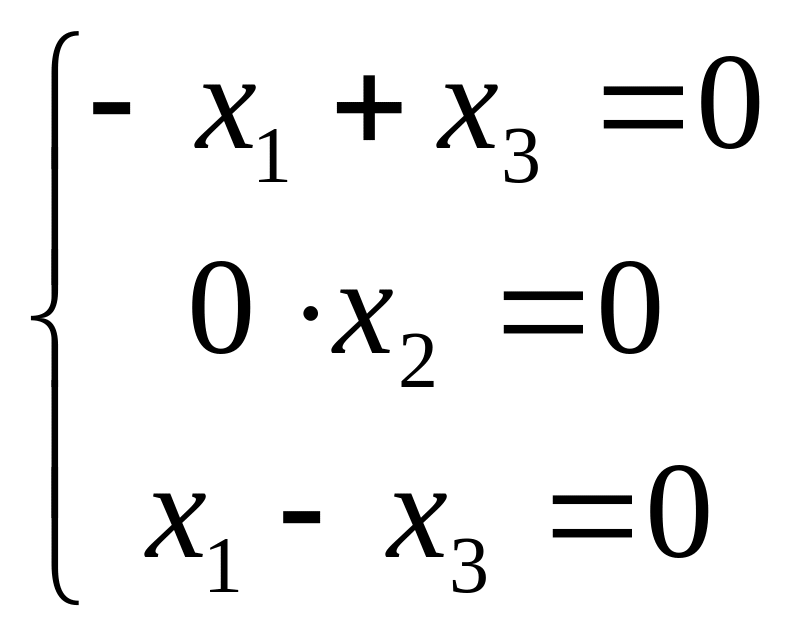 ,
которая эквивалентна двум уравнениям
,
которая эквивалентна двум уравнениям
![]() .
Очевидно, второе уравнение системы
обращается в тождество при всех значениях
.
Очевидно, второе уравнение системы
обращается в тождество при всех значениях
![]() .
Положив
.
Положив
![]() ,
найдем из первого уравнения
,
найдем из первого уравнения
![]() ,
что дает собственный вектор
,
что дает собственный вектор
![]() .
Поскольку свободных переменных две,
полагая
.
Поскольку свободных переменных две,
полагая
![]() ,
а
,
а
![]() и
и
![]() ,
а
,
а
![]() найдем два собственных вектора,
соответственно,
найдем два собственных вектора,
соответственно,
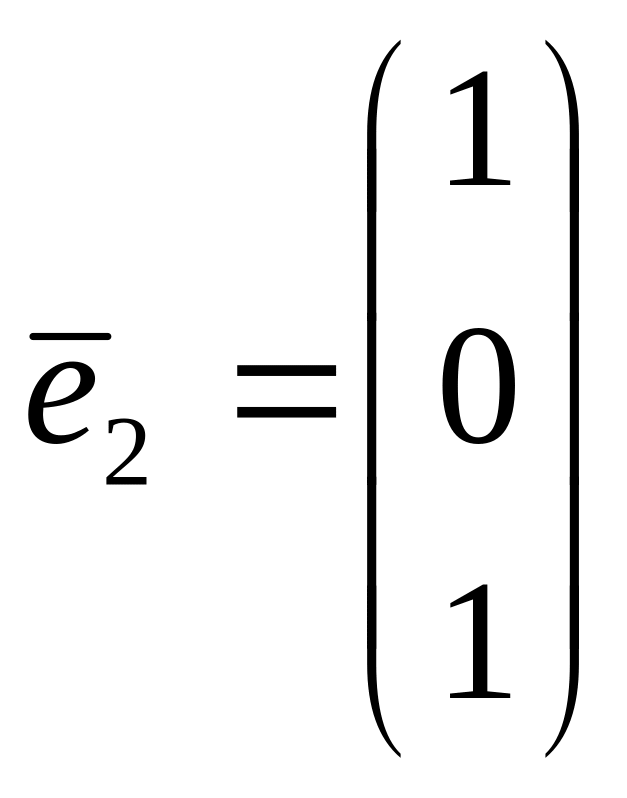 и
и
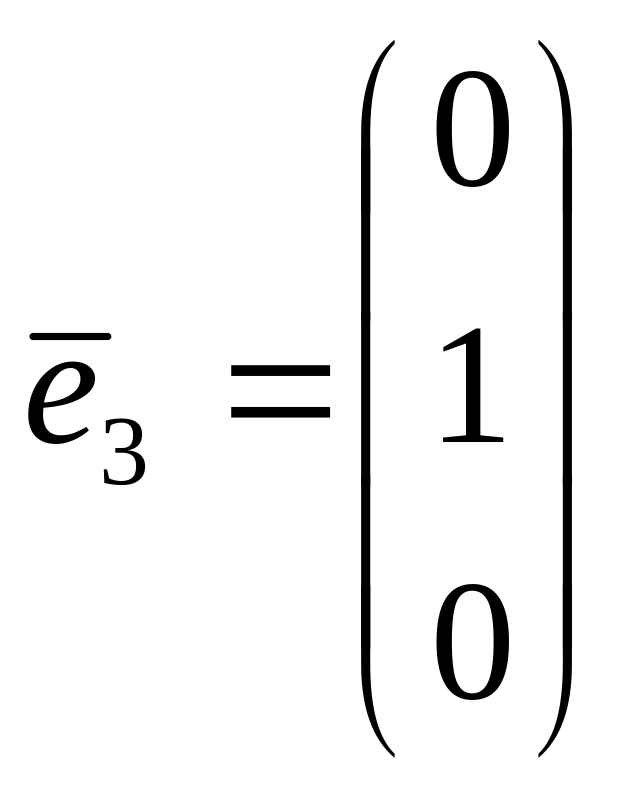 .
.
Ответ. Собственному значению
соответствует собственный вектор
,
а векторы
и,
соответствуют кратным собственным
значениям
![]() .
.
