
- •Линейная алгебра
- •Введение
- •1. Операции над матрицами
- •2. Линейные преобразования и матрицы
- •Обратная матрица. Решение систем линейных уравнений матричным способом
- •Ранг матрицы. Решение систем линейных уравнений
- •Собственные числа и собственные векторы квадратной матрицы
- •Приведение квадратичной формы к каноническому виду
- •Решение однородных систем линейных дифференциальных уравнений с постоянными коэффициентами
- •Характеристика задания
- •Варианты контрольных заданий
- •Вариант № 5
- •Вариант №6
- •Вариант № 7
- •Вариант № 8
- •Вариант №9
- •Вариант № 10
- •Вариант № 11
- •Вариант №12
- •Вариант № 13
- •Вариант № 14
- •Вариант №15
- •Вариант №16
- •Вариант №17
- •Вариант №18
- •Вариант №19
- •Вариант № 20
- •Вариант № 21
- •Вариант № 22
- •Вариант № 23
- •Вариант № 24
- •Вариант № 25
- •Библиографический список
- •Оглавление
- •Линейная алгебра
- •394006 Воронеж, ул. 20-летия Октября, 84
2. Линейные преобразования и матрицы
Преобразование, в котором новые координаты (со штрихом) выражаются через старые координаты линейным образом
 (5)
(5)
называется линейным. Очевидно, каждому линейному преобразованию (5) соответствует квадратная матрица
А =
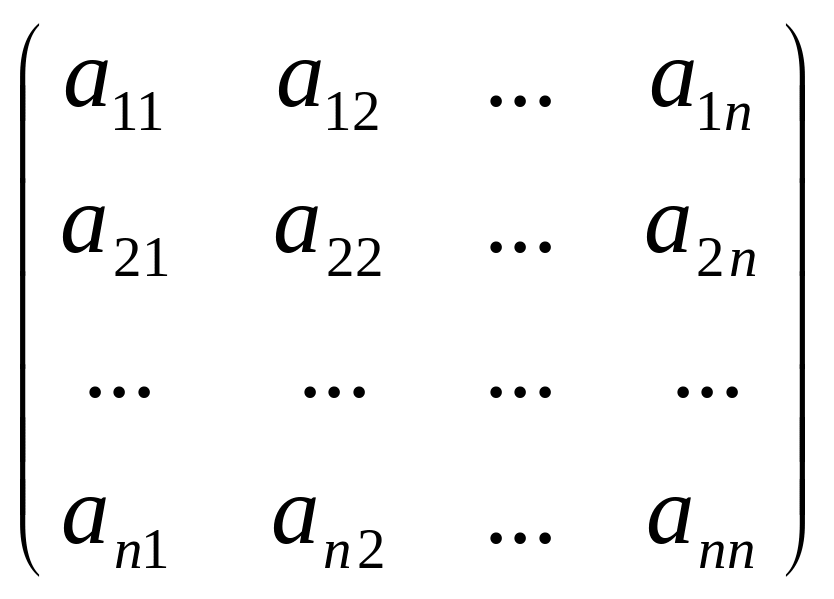 , (6)
, (6)
Если еще ввести векторы-столбцы
![]() и
и
![]() ,
то преобразование (5) в матричной форме
примет вид
,
то преобразование (5) в матричной форме
примет вид
![]() . (7)
. (7)
Из линейных свойств матрицы следуют свойства аддитивности и однородности линейного преобразования (5):
![]() ,
, ![]() . (8)
. (8)
Если заданы два линейных преобразования
и
![]() ,
то суперпозиция линейных преобразований,
выражающие координаты
,
то суперпозиция линейных преобразований,
выражающие координаты
![]() через неизвестные
через неизвестные
![]() задаются матрицей
задаются матрицей
![]() . (9)
. (9)
Легко проверить, что вектор
![]() ,
который является
,
который является
первым столбцом матрицы
![]() ,
является образом единичного орта
,
является образом единичного орта
![]() :
:
![]() .
Аналогично,
.
Аналогично,
![]() задает второй столбец матрицы и т.д. В
силу линейных свойств матрицы
она переводит вектор
задает второй столбец матрицы и т.д. В
силу линейных свойств матрицы
она переводит вектор
![]() в вектор
в вектор
![]() ,
т.е. ортонормированный базис
,
т.е. ортонормированный базис
![]() в базис
в базис
![]() (для невырожденных матриц, определитель
которой не равен нулю
(для невырожденных матриц, определитель
которой не равен нулю
![]() ).
Из геометрического смысла смешанного
произведения следует геометрический
смысл модуля определителя матрица А
– коэффициент изменения объема при
данном преобразовании. Аналогично, на
плоскости единичный квадрат, построенный
на векторах
).
Из геометрического смысла смешанного
произведения следует геометрический
смысл модуля определителя матрица А
– коэффициент изменения объема при
данном преобразовании. Аналогично, на
плоскости единичный квадрат, построенный
на векторах
![]() переходит в параллелограмм, построенный
на векторах
переходит в параллелограмм, построенный
на векторах
![]() и
и
![]() ,
а
,
а
![]() .
Основными типами линейных преобразований
на плоскости являются преобразования
гомотетии (подобие с центром в начале
координат), поворот на угол
.
Основными типами линейных преобразований
на плоскости являются преобразования
гомотетии (подобие с центром в начале
координат), поворот на угол
![]() вокруг начала координат и симметрии.
Матрица гомотетии с коэффициентом
подобия
вокруг начала координат и симметрии.
Матрица гомотетии с коэффициентом
подобия
![]() имеет вид
имеет вид
![]() ,
где
,
где
![]() единичная матрица. В случае диагональной
матрицы вида
единичная матрица. В случае диагональной
матрицы вида
![]() ,
при
,
при
![]() ,
,
![]() ,
являющуюся обобщением матрицы
,
являющуюся обобщением матрицы
![]() ,
где
,
где
![]() ,
является преобразованием растяжения
,
является преобразованием растяжения
![]() ,
или сжатия
,
или сжатия
![]() ,
,
![]() 2 по соответствующей
оси.
2 по соответствующей
оси.
Матрица поворота
![]() на угол
вокруг начала координат имеет вид
на угол
вокруг начала координат имеет вид
![]() . (10)
. (10)
Отметим, что матрицы поворота перестановочны между собой т.е.
![]() .
.
Пример 3. Написать матрицу симметрии С относительно прямой y=x.
Решение. Симметрия относительно
биссектрисы в 1-ом и 3-ем координатных
углах переводит ось OX
в ось OY и наоборот,
следовательно,
![]() ,
,
![]() .
Соединив найденные 1-ый и 2-ой столбцы,
получим
.
Соединив найденные 1-ый и 2-ой столбцы,
получим
![]() .
.
Отметим, что ее определитель
![]() .
В общем случае, любое линейное
преобразование на плоскости является
комбинацией вышеперечисленных типов,
а если определитель отрицателен, то в
этом преобразовании будет участвовать
симметрия относительно некоторых
прямых.
.
В общем случае, любое линейное
преобразование на плоскости является
комбинацией вышеперечисленных типов,
а если определитель отрицателен, то в
этом преобразовании будет участвовать
симметрия относительно некоторых
прямых.
Пример 4. Определить геометрическое
преобразование, заданное матрицей
![]() .
.
Решение. Заметим, что
![]() ,
аналогично,
,
аналогично,
![]() .
Следовательно, данное преобразование
по оси Оx задает
растяжение в 3 раза, а по оси Oy
– сжатие в 2 раза.
.
Следовательно, данное преобразование
по оси Оx задает
растяжение в 3 раза, а по оси Oy
– сжатие в 2 раза.
Пример 5. Указать матрицу линейного
преобразования D в
пространстве, которое выполняет поворот
векторов вокруг оси Oz
на угол
![]() .
.
Решение. Так как ось Oz
остается на месте, то
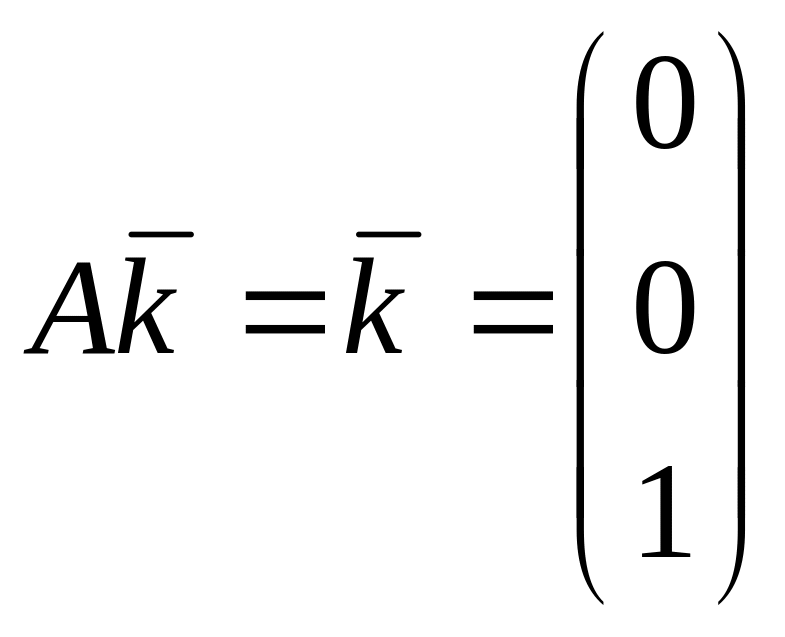 .
При этом проекции вектора в плоскости
xOy должны поворачиваться
на угол
,
тогда
.
При этом проекции вектора в плоскости
xOy должны поворачиваться
на угол
,
тогда
![]()
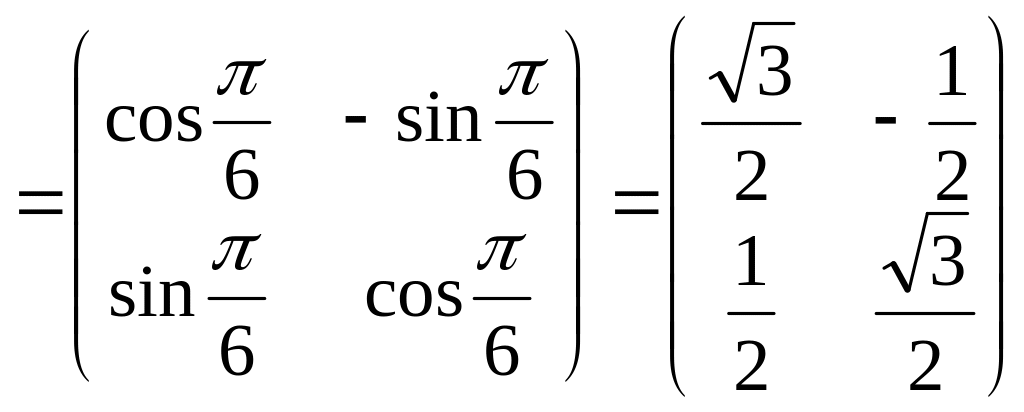 .
Окончательно получим D=
.
Окончательно получим D= .
.
Пример 6. Даны два линейных
преобразования на плоскости
![]() ,
,
![]() .
Найти преобразование, преобразующее
вектор
.
Найти преобразование, преобразующее
вектор
![]() в
в
![]() .
.
Решение. Выпишем матрицы преобразований
![]() и
и
![]() ,
тогда по формуле (9)
,
тогда по формуле (9)
![]()
![]() .
.
Вернувшись к неизвестным укажем
результирующее преобразование,
соответствующее матрице С:
![]() .
.
