
- •1. Основные понятия теории дифференциальных уравнений
- •3. Определение общего, частного и особого решения
- •4. Геометрическая интерпретация дифференциального уравнения. Метод изоклин
- •5. Задачи, приводящие к дифференциальным уравнениям
- •6. Уравнения с разделяющимися переменными
- •Пример 4. Найти общий интеграл дифференциального уравнения
- •7. Однородные дифференциальные уравнения первого порядка и уравнения, приводящиеся к ним
- •Решение. Запишем уравнение в виде
- •Откуда, разделяя переменные
- •И, интегрируя, находим
- •Уравнение примет вид
- •Разделяем переменные, тогда
- •Интегрируя
- •8. Линейные уравнения и уравнения, приводящиеся к ним
- •Решение уравнения (8.1) находят в виде
- •Откуда, выполняя замену и интегрируя по частям, находим
- •Следовательно, общим решением будет функция
- •9. Уравнения Бернулли и Риккати
- •10. Дифференциальные уравнения в полных дифференциалах
- •11. Интегрирующий множитель
- •12.Уравнения, неразрешенные относительно производной
- •Отыскание решений уравнений вида
- •1. Пусть уравнение (12.1) удается разрешить относительно производной, тогда (12.1) распадается на уравнения вида
- •13. Уравнения Лагранжа и Клеро
- •14. Теорема существования и единственности решения задачи Коши
- •Интегрируя его в пределах от до тождество
- •Таким образом, удовлетворяет интегральному уравнению при
- •4.Краснов м.Л. Обыкновенные ифференциальные
- •Часть 2. «Специальные разделы математического анализа» (под редакцией а.В. Ефимова, б.П. Демидовича). М., Наука,
- •1. Основные понятия теории дифференциальных уравнений …………………………………………………….4
- •394026 Воронеж, Московский просп., 14
Откуда, выполняя замену и интегрируя по частям, находим
![]() .
.
Следовательно, общим решением будет функция
![]() .
.
9. Уравнения Бернулли и Риккати
К линейным уравнениям приводятся и уравнения вида
![]() ,
,
называемые уравнениями Бернулли. Достаточно сделать
замену
![]() .
Однако, решение уравнения Бернулли
удобнее искать в виде
,
не приводя к линейному.
.
Однако, решение уравнения Бернулли
удобнее искать в виде
,
не приводя к линейному.
Аналогично тому, как в анализе при интегрировании элементарных функций появляются интегралы, не выражающиеся через элементарные функции, тем самым порождающие новый класс трансцендентных функций, т и большинство дифференциальных уравнений не интегрируются в конечном виде, а их решения порождают новый еще более высокий класс трансцендентных функций. Классификация новых трансцендентных функций, являющихся решениями дифференциального уравнения, и выяснение той или иной их природы есть одна из главных задач теории дифференциальных уравнений.
Уравнение Риккати
![]()
является именно таким
уравнением, в общем случае не интегрируемым
в квадратурах. Но если известно одно
частное решение
![]() ,
то заменой
,
то заменой
![]() уравнение Рикатти сводится к уравнению
Бернулли. Частное решение иногда можно
подобрать, исходя из вида свободного
члена уравнения.
уравнение Рикатти сводится к уравнению
Бернулли. Частное решение иногда можно
подобрать, исходя из вида свободного
члена уравнения.
Например, для уравнения
![]()
Частное решение будем
искать у в виде
![]() .
Подставляя в уравнение, находим
.
Подставляя в уравнение, находим
![]() и
и
![]() .
Замена
.
Замена
![]() приводит исходное уравнение к уравнению
Бернулли
приводит исходное уравнение к уравнению
Бернулли
![]() .
.
Решая стандартными методами это уравнение, получаем общее решение
![]()
и
![]() - особое решение, существование которого
является следствием нарушения
непрерывности в правой части уравнения
при
- особое решение, существование которого
является следствием нарушения
непрерывности в правой части уравнения
при
![]() .
.
Пример 1. Найти общее решение уравнения Бернулли:
![]() .
.
Решение.
Положим
![]() .
Тогда будем иметь
.
Тогда будем иметь
![]() .
.
Функцию
v(x)
найдём как частное решение уравнения
![]() .
Имеем
.
Имеем
![]() .
Тогда
.
Тогда
![]() .
Откуда, разделяя переменные и интегрируя,
получим
.
Откуда, разделяя переменные и интегрируя,
получим
![]() .
.
Таким образом,
![]() .
.
А общее решение уравнения будет иметь вид
![]() .
.
Пример 2. Найти решение задачи Коши
+
![]() = xy2
, y(0)=1.
= xy2
, y(0)=1.
Решение.
Уравнение
Бернулли будем интегрировать с помощью
подстановки
.
Тогда
![]() .
И после подстановки первоначальное
уравнение примет вид:
.
И после подстановки первоначальное
уравнение примет вид:
![]() +uv
= xu2v2
(8.7)
+uv
= xu2v2
(8.7)
Найдем
функцию
![]() из условия
из условия

Из общего решения выберем одно частное решение v = e-x , подставляя его в уравнение (8.7), получим уравнение относительно функции u = u(x)
![]()
Это уравнение является уравнением с разделяющимися переменными. Решаем его
![]() ,
,

Следовательно, общее решение первоначального уравнения имеет вид
![]() .
.
Для того, чтобы найти С, воспользуемся начальным условием.
![]()
Следовательно, решение задачи Коши будет иметь вид
![]() или
или
![]() .
.
Пример 3. Найти
общее решение уравнения
.
![]() .
.
Решение.
Это – уравнение Бернулли. Проинтегрируем
его методом вариации произвольной
постоянной. Для этого интегрируем
сначала соответствующее линейное
однородное уравнение
![]() ,
решение которого
,
решение которого
![]() .
.
Ищем решение исходного уравнения Бернулли, полагая
![]() ,
,
![]() .
.
Подстановка
![]() и
и
![]() в исходное уравнение дает
в исходное уравнение дает

или
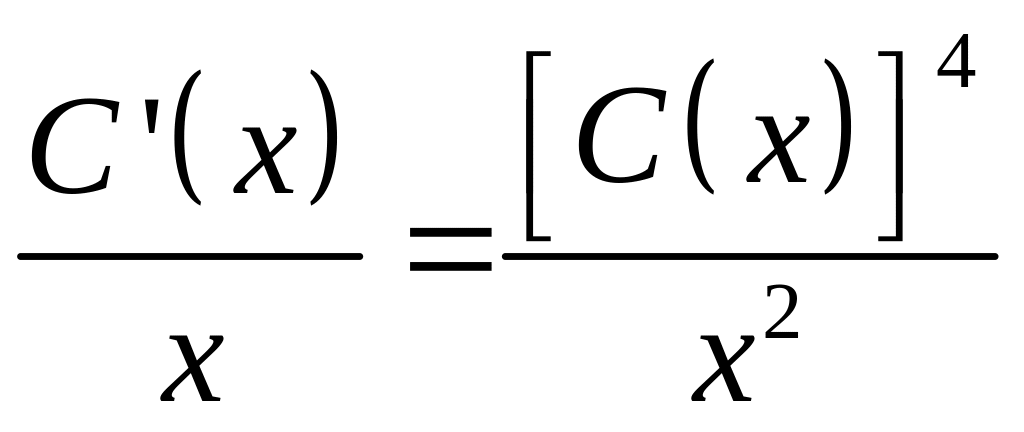 .
.
Для
определения
![]() интегрируем
полученное уравнение
интегрируем
полученное уравнение
 ;
;
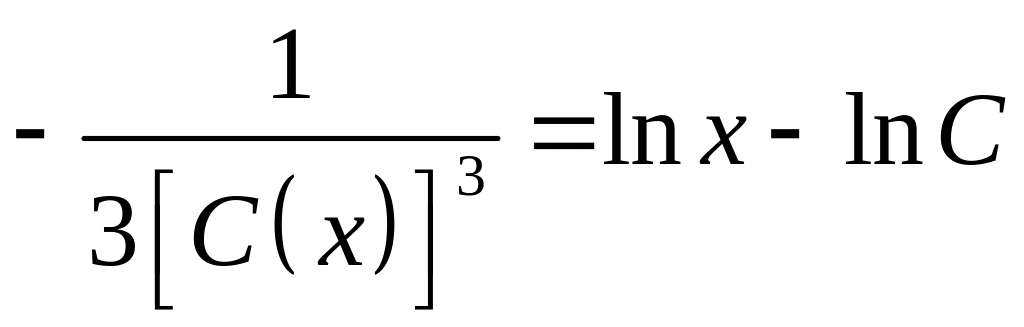 ;
;
 .
.
Следовательно общее решение будет иметь вид

