
- •1. Основные понятия теории дифференциальных уравнений
- •3. Определение общего, частного и особого решения
- •4. Геометрическая интерпретация дифференциального уравнения. Метод изоклин
- •5. Задачи, приводящие к дифференциальным уравнениям
- •6. Уравнения с разделяющимися переменными
- •Пример 4. Найти общий интеграл дифференциального уравнения
- •7. Однородные дифференциальные уравнения первого порядка и уравнения, приводящиеся к ним
- •Решение. Запишем уравнение в виде
- •Откуда, разделяя переменные
- •И, интегрируя, находим
- •Уравнение примет вид
- •Разделяем переменные, тогда
- •Интегрируя
- •8. Линейные уравнения и уравнения, приводящиеся к ним
- •Решение уравнения (8.1) находят в виде
- •Откуда, выполняя замену и интегрируя по частям, находим
- •Следовательно, общим решением будет функция
- •9. Уравнения Бернулли и Риккати
- •10. Дифференциальные уравнения в полных дифференциалах
- •11. Интегрирующий множитель
- •12.Уравнения, неразрешенные относительно производной
- •Отыскание решений уравнений вида
- •1. Пусть уравнение (12.1) удается разрешить относительно производной, тогда (12.1) распадается на уравнения вида
- •13. Уравнения Лагранжа и Клеро
- •14. Теорема существования и единственности решения задачи Коши
- •Интегрируя его в пределах от до тождество
- •Таким образом, удовлетворяет интегральному уравнению при
- •4.Краснов м.Л. Обыкновенные ифференциальные
- •Часть 2. «Специальные разделы математического анализа» (под редакцией а.В. Ефимова, б.П. Демидовича). М., Наука,
- •1. Основные понятия теории дифференциальных уравнений …………………………………………………….4
- •394026 Воронеж, Московский просп., 14
5. Задачи, приводящие к дифференциальным уравнениям
Дифференциальные равнения являются математической моделью многочисленных физических, химических, биологических и др. процессов. При составлении дифференциальных уравнений весьма часто используют физические законы, которые описывают соотношение между величинами, характеризующими изучаемый процесс, и скоростью изменения этих величин. Например, в механике – законы Ньютона, в теории электрических цепей – законы Кирхгоффа, в теории скоростей химических реакций – закон действия масс и т.д. Если физический закон протекания процесса неизвестен, то для составления дифференциального уравнения прибегают к гипотезе о линейности процесса “в малом”, т.е., например, считают, что в течение малого промежутка времени ∆t участвующие в процессе величины изменяются с постоянной скоростью. Составляют соотношения между приращениями этих величин и, переходя к пределу при ∆t→0, получают уравнение, содержащее производную по времени. Дифференциальное уравнение – это как бы “мгновенный снимок процесса” в данный момент времени, интегрируя дифференциальное уравнение, мы по мгновенным снимкам восстанавливаем течение процесса в целом.
Задача 1. Пусть в резервуаре имеется a кг водного раствора соли, в котором содержится b кг соли. В определенный момент включается устройство, непрерывно подающее в резервуар с кг чистой воды в секунду и одновременно удаляющее из него ежесекундно с кг раствора. При этом в самом резервуаре жидкость непрерывно перемешивается. Как изменяется количество соли в резервуаре?
Решение.
Примем за
начало отсчета момент t.
Пусть y(t)
– искомая функция, выражающая в каждый
момент времени t
количество соли в резервуаре. В силу
условия задачи и соглашения об отсчете
времени, y(0)=b.
За малый промежуток [t,t+∆t]
из резервуара с раствором выльется
(y(t)-(y(t+t)))
кг соли. Так как концентрация в
рассмотренный промежуток времени
убывала от
![]() до
до
![]() ,
то
,
то
![]() ,
,
причем неравенства являются строгими, если c0, b0, разделив это неравенство на t, получим
![]()
Исходя из характера рассматриваемого процесса, можно заключить, что y(t) – непрерывна, значит,
![]()
В результате получаем
![]()
т. е. y(t) удовлетворяет дифференциальному уравнению
![]()
С учетом начального условия y(0)=b решение этого уравнения имеет вид
![]()
Полученная формула показывает, что процесс опреснения раствора в резервуаре происходит по экспоненциальному закону.
Таким образом, дифференциальное уравнение, моделируя процесс, описывает эволюцию процесса, показывает характер происходящих с материальной системой изменений. При этом не обязательно изменения происходят во временном промежутке.
Приведем пример вывода уравнений из других областей естествознания, приводящих к экспоненциальному закону.
Задача 2. При определении давления воздуха над уровнем моря в зависимости от высоты p(h) поступают следующим образом. Рассматривают два горизонтальных сечения столба воздуха на высоте h и h+h, опирающегося на площадку размером 1м2. Давление на высоте h+h будет меньше на величину p, равную весу воздуха в столбе между двумя сечениями: p=dh, где d – вес одного кубометра воздуха при давлении p. Полагая, что во всех сечениях между h и h+h давление постоянно в силу закона Бойля – Мариотта, получают d= k p, где k – коэффициент пропорциональности. Выполняя деление на h в равенстве p=- k ph и переходя к пределу при h0, получают дифференциальное уравнение
![]() .
.
Приведем еще один пример использования физического закона при составлении дифференциального уравнения.
Задача 3. Пусть требуется узнать, за какое время упадет на поверхность Луны камень с высоты h. Пусть x(t) – высота камня над поверхностью в момент времени t.
Решение. Согласно закону свободного падения, открытому Г.Галилеем, все тела, независимо от их массы, падают в поле силы тяжести с постоянным ускорением a,
( для поверхности луны а=1/6g),
следовательно,
![]() Интегрируя дважды, находим
Интегрируя дважды, находим
![]()
Постоянные
С1,
С2
находим из условий х(0)=0,
и х(0)=h.
Функция
![]() описывает закон движения камня. Моменту
удара t
камня о поверхность соответствует
x(t)=0,
поэтому ответ задачи
описывает закон движения камня. Моменту
удара t
камня о поверхность соответствует
x(t)=0,
поэтому ответ задачи
![]() .
.
Задача
4. Найти
линию, проходящую через точку
![]() ,
если отрезок любой ее касательной между
точкой касания и осью делится в
точке пересечения с осью абсцисс в
отношении
,
если отрезок любой ее касательной между
точкой касания и осью делится в
точке пересечения с осью абсцисс в
отношении
![]() (считая
от оси
(считая
от оси
![]() ).
).
Решение. При решении геометрических задач можно использовать уравнение касательной:
![]()
где
![]() –
координаты произвольной точки искомой
линии, а (Х,У) – координаты точки, лежащей
на касательной. Иногда удобнее исходить
из геометрического смысла производной.
В данной задаче достаточно заметить,
что
–
координаты произвольной точки искомой
линии, а (Х,У) – координаты точки, лежащей
на касательной. Иногда удобнее исходить
из геометрического смысла производной.
В данной задаче достаточно заметить,
что
 .
Откуда
и получаем дифференциальное уравнение
.
Откуда
и получаем дифференциальное уравнение
 .
.
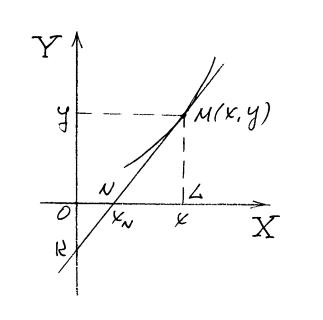
рис .5
Можно
рассуждать иначе. По
условию задачи
![]() .
Треугольники
.
Треугольники
![]() и
и
![]() –
подобны. Следовательно,
–
подобны. Следовательно,
![]()
Откуда находим
![]()
Точка
![]() принадлежит
касательной, поэтому
принадлежит
касательной, поэтому
![]()
Подставляя
выражение для
![]() в
предыдущее равенство, получаем
дифференциальное уравнение первого
порядка:
в
предыдущее равенство, получаем
дифференциальное уравнение первого
порядка:

Так как, линия проходит через точку , то подставляя в общее решение координаты точки, получаем значение константы
![]()
Окончательно, получаем уравнение искомой линии
![]()
Рассмотрим
простейшие и наиболее распространенные
в приложениях случаи, когда решение
уравнения
![]() может быть выражено через элементарные
функции или интегралы от них.
может быть выражено через элементарные
функции или интегралы от них.
