14. Теорема существо­вания и единственности решения задачи Коши

Приступим к доказательству одной из важнейших теорем тео­рии дифференциальных уравнений, которая утверждает существо­вание и единственность решения задачи Коши локально, вблизи начальной точки х₀.

Вспомогательные леммы.

1. Интегральным уравнением называется соотношение вида

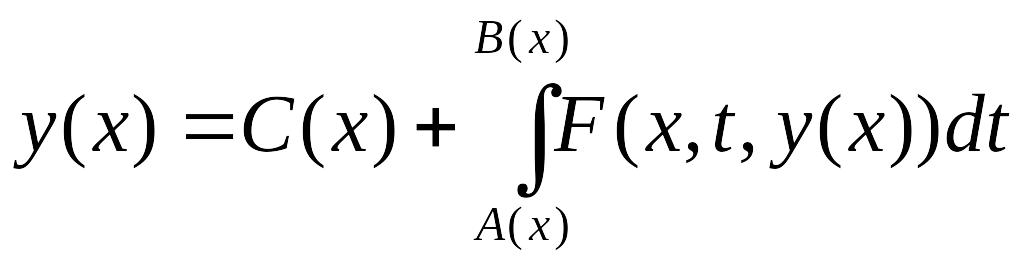
где у(х)— искомая функция, F(x, t, у), А(х), В(х), С(x) —задан­ные функции. Непрерывная функция y = , определенная в некотором промежутке и обращающая там написанное соотно­шение в тождество, называется решением интегрального уравнения.

Оказывается полезным свести решение задачи Коши к реше­нию интегрального уравнения.

Лемма 1 . Решение y = задачи Коши

определенное в некотором промежутке , содержащем точку х₀ , является решением интегрального уравнения

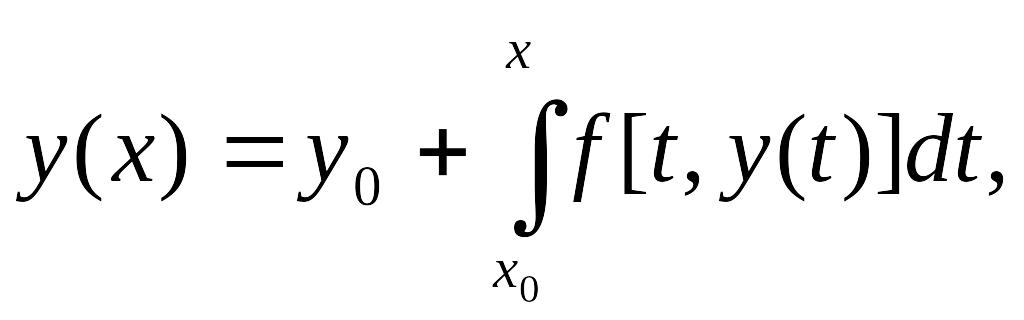
Наоборот, непрерывное на (α, β), решение интегрального уравнения является решением задачи Коши.

Доказательство. Пусть — решение задачи Коши, — непрерывная функция (так как она обладает непрерывной производной), f [x, ] —также непрерывная функция.

Интегрируя его в пределах от до тождество

φ'(x) ≡ f [x, φ(x)],

получим

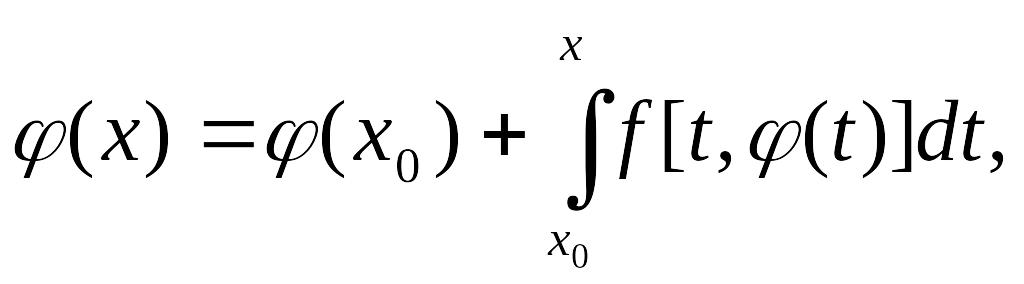
Таким образом, удовлетворяет интегральному уравнению при

Наоборот, если непрерывная на функция φ(х) удовлет­воряет интегральному уравнению, то, очевидно, и по теореме о производной интеграла по верхнему пределу получим

φ'(x) = f [x, φ(x)],

Следовательно, является решением задачи Коши.

Определение 1. Мы говорим, что функция f(x, у) с областью определения удовлетворяет на условию Липшица по переменной у, если существует постоянная L, 0≤L<∞, такая, что для любых двух точек (х, y₁), (х, y₂) из выполняется неравенство

При этом, постоянная L называется константой Липшица функции f(x, у) на множестве .

Класс функций, удовлетворяющих на условию Липшица по y, будем обозначать через Lip ; тот его подкласс, для кото­рого неравенство выполняется именно с постоянной L, —через Lip .

Лемма 2. Пусть функция f(x, у), заданная в открытой области G непрерывна и обладает непрерывной про­изводной в G. Тогда на любом ограниченном подмножестве из G, замыкание которого принадлежит G, функция f(х, у) удов­летворяет условию Липшица

где постоянная L зависит, вообще говоря, от .

Доказательство: Возьмем вна­чале в качестве прямоугольник

с центром в точке (х₀, у₀), целиком содержащийся в области Тогда по теореме о среднем для любых точек (х, y₁), (х, y₂) П

где

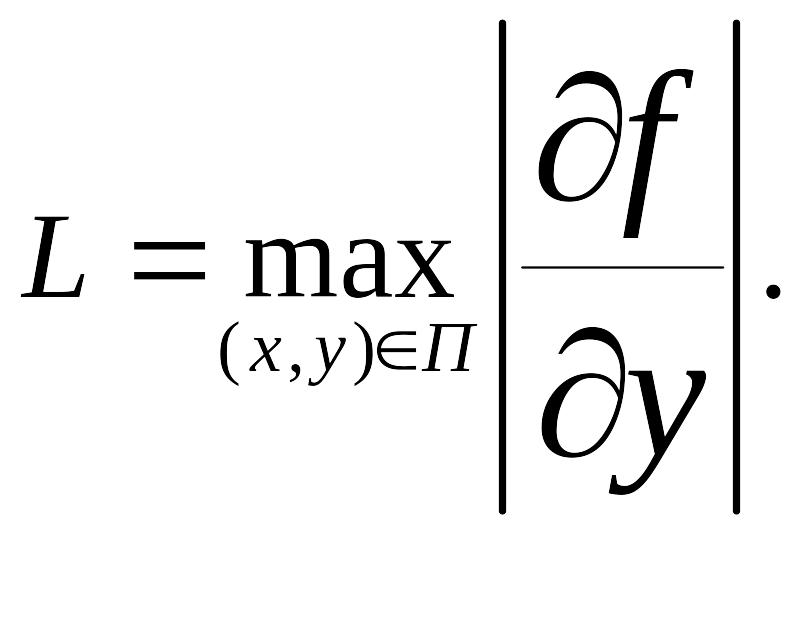
Замечание. Доказанную лемму можно описательно выразить словами: из существования непрерывной производной следует, что функция f удовлетворяет условию Липшица по у. Обратное утверждение неверно: из липшицевости по у не следует существования производной по у (тем более непрерывной произ­водной по у). Пример 2. Рассмотрим функцию f(х, у) = | у | .

Ясно, что

и, таким образом, f(x, у) удовлетворяет условию Липшица по у с постоянной L=1. Однако производная не существует в точке (х, 0).

Теорема 1( Коши - Пикара). Пусть функция f (x, у) определена в прямоугольнике

непрерывна в П и удовлетворяет условию Липшица по у. Тогда дифференциальное уравнение

y'=f(x, y) (14.1)

имеет решение у=φ(х), удовлетворяющее начальному условию

у(х_о)=у_{о ,} (14.2)

определенное в промежутке , где

.

Это решение единственно в том смысле, что любое другое ре­шение уравнения (1), удовлетворяющее тому же начальному условию

совпадает с φ(х) в том промежутке, где оба решения определены одновременно.

Доказательство. По лемме об эквивалентности вместо задачи Коши

можно рассматривать задачу нахождения реше­ния интегрального уравнения

Будем искать решение последнего методом последовательных при­ближений. Построим последовательность функций, определенных, как мы сейчас увидим, по крайней мере при :

,

,

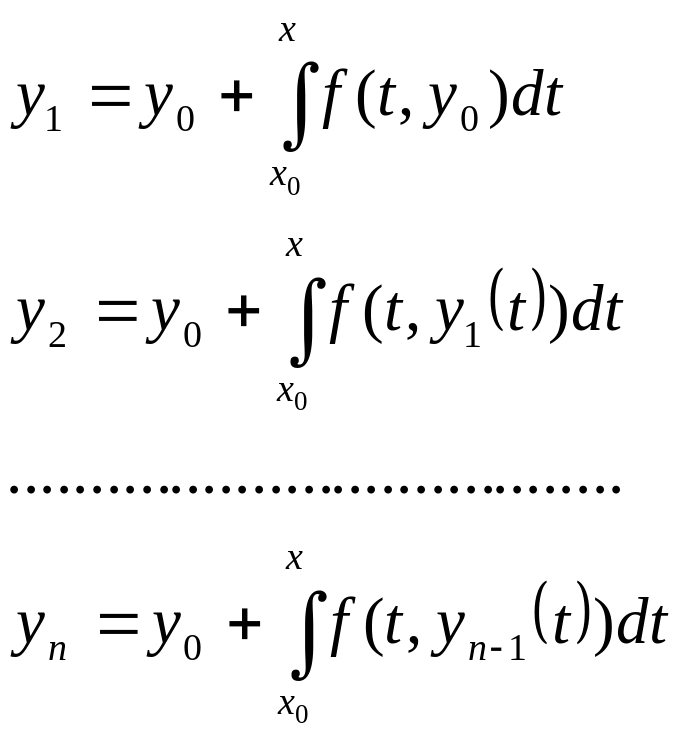Убедимся, что члены последовательности не выходят при из прямоугольника П. В противном случае наши построения незаконны, так как функция f(x, у) определена лишь в П, а мы рассматриваем величину

f ( t , y _n ( t ).

Имеем оценку

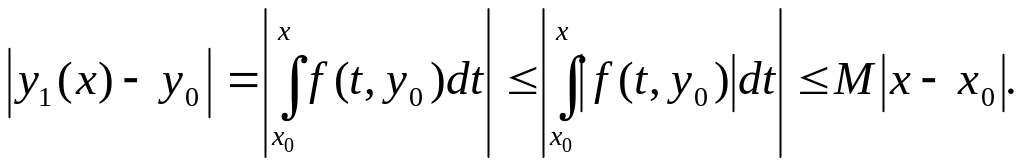(14.3)

Отсюда видно, что если , то ,

т. е. не выходит из П. Таким образом, х подчинено требованиям , и если положить то оба требования будут удовлетворены при . Будем считать неравенство выполненным. Пользуясь им, получим

и, следовательно, в промежутке члены последова­тельности не выходят из П.

Из дальнейшего будет видно, что с возрастанием п функции у_п (х) приближаются к решению. Будем называть эти функции последовательными приближениями к решению.

Поясним геометрически ограничение , возникшее при построении последовательных приближений. Дело в том, что, поскольку , искомая интегральная кривая у = , проходящая через точку (х₀,у₀), обязана располагаться внутри угла, образованного пря­мыми

(14.4)

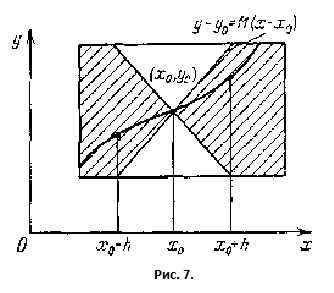
(заштрихованного на рис. 6). Если бы она пересекла одну из указан­ных прямых, то в точке пересече­ния (или вблизи нее) имело бы место неравенство , что невозможно. Точки встречи пря­мых (13.4) со сторонами прямо­угольника П, будучи спроектиро­ваны на ось Ох, определяют проме­жуток , в котором ре­шение «наверняка» определено.

Вопрос о сходимости последовательности сведем к рас­смотрению сходимости ряда

(14.5)

По условию теоремы функция f(x, у) удовлетворяет в

П усло­вию Липшица по у, т. е. существует постоянная L

такая, что

(14.6)

для любых (х, y₁), (х, y₂) П .

По вышесказанному имеет место оценка

По условию Липшица и в силу этой оценки получим

Рассуждая по индукции, предположим, что

(14.7)

и проверим, что подмеченный закон остается верным при пере­ходе от n к n+1. Имеем

Таким образом, обоснована оценка (14.7) общего члена ряда (14.5). Из нее следует равномерная сходимость ряда (14.5) к своей сумме, которую обозначим через при .

В самом деле, члены ряда (14.5) по абсолютной величине не превосходят членов сходящегося числового ряда

и, следовательно, выполнен мажорантный признак Вейерштрасса равномерной сходимости ряда (14.5). Так как п-я частная сумма ряда (14.5) совпадает с у_п(х), то у_п(х) равномерно сходится к при .

Поскольку функции у_п (х) непрерывны, то и предельная функция непрерывна.

Мы доказали, что последовательность сходится рав­номерно к непрерывной функции φ(х) в промежутке . Чтобы доказать, что функция φ(х) представляет собой искомое решение, достаточно убедиться, что предельный переход при в равенстве

(14.8)

приводит к равенству

(14.9)

(т. е. обосновать предельный переход под знаком интеграла).

Законность такого перехода следует из оценки

Неравенство (14.6) в данном случае применимо; очевидно, что точка (х, ) не выходит из П при (следует пе­рейти к пределу при в неравенстве ). В силу равномерной сходимости у_п к φ можно выбрать N так, что при n>N будем иметь (и, таким образом, оце­ниваемая величина не превзойдет ε). Следовательно, при из (14.8) получается (14.9).

Пример 1. Оценить ошибку приближения в задаче при

Указание: Оценить остаток ряда, сходимость которого доказывается в теореме существования решений.

Решение. В данном случае функция непрерывно дифференцируема по y и ее частная производная по y есть . Поэтому удовлетворяет условию Липшица :

.

Найдем третье приближение, оно будет находиться в виде:

Имеем:

Ошибка приближения между точным решением и n-м приближением оценивается следующим неравенством, полученным при доказательстве теоремы существования

где L – постоянная Липшица, .

Найдем постоянную L из условия Липшица

Подставим x = 0.5 , получим .

Тогда найдем ошибку приближения между точным решением и третьим приближением _.

15. Понятие полного решения

Напомним, что открытой окрестностью точки называют произвольную открытую область, содержащую точку, и просто окрестностью — открытую окрестность, к которой присоединена часть граничных точек или же вся граница (в последнем случае будем говорить о замкнутой окрестности). По этой терминологии прямоугольник является (замкнутой) окрестностью точки

В реальных условиях функция f(x, у) бывает определена в некоторой области G на плоскости (отличной от прямоугольника) и начальная точка расположена в области G про­извольно. Если область G — открытая, то принадлежит G вместе с некоторой прямоугольной окрестностью , при­чем размеры а, b этого прямоугольника стеснены требованием . Если функция f(x, у) непрерывна в области G вме­сте с производной , то в П выполняются условия теоремы Коши-Пикара и «вблизи» точки определено решение у= задачи Коши

y'= f(x, у) , y(х_о)=y_0.

Таким образом, утверждения теоремы Коши-Пикара имеют локальный ха­рактер. На самом деле решение определено в более широком промежутке. Возникает вопрос об описании «полного» проме­жутка определения решения и свойствах этого «полного» реше­ния.

Если функция f(x, у) задана в полосе

то теорема существования дает по существу описание полной области определения решения. Этот случай важен, поскольку он охватывает линейные дифференциальные уравнения (и соответствующий результат обобщается на системы таких уравнений).

Теорема 2. Пусть функция f(x, у) определена и непре­рывна в полосе Q и удовлетворяет в Q условию Липшица по у:

(15.1)

Тогда при произвольно фиксированных начальных данных , , существует единственное решение задачи Коши

y'= f(x, у) , y(х_о)=y_0. (15.2)

определенное на всем отрезке и ограниченное на нем.

16. Продолжение решения

Пусть решение уравнения y'= f(x, у), f C(G), определено в промежутке (a, b), a другое решение — в промежутке (А, В), причем (a, b) есть часть (А, В) и

.

Тогда решение φ(х) называется продолжением решения ψ(x) с промежутка (а, b) на промежуток (А, В) (говорят также, что φ(х) допускает продолжение ψ(x)), а φ(х) — называется сужением ψ(x) на (а, b). Если же промежутки (a, b) и (А, В) пересекаются по промежутку (с, d), c<d, и то мы говорим, что φ(х) и ψ(x) являются продолжением одна другой из промежутка (с, d). Ясно, что в этом случае функция

будет решением уравнения в . В случае, если c=d и промежуток (с, d) вырождается в точку, мы говорим о «стыковке» решений φ и ψ. Стыковка решений, очевидно, также представляет решение.

Определение. Решение у = у(х) дифференциального урав­нения

с областью определения (α,β) называется непродолжаемым, если не существует решения с более широкой областью определе­ния (а, b), сужение которого на совпадало бы с φ(х).

Сказанное означает, что область определения непродолжимого решения у= обладает свойством максимальности: для всякого решения ψ(x) с областью определения (а, b), совпа­дающего с там, где φ и ψ определены одновременно, (а, b) есть часть .

Как уже говорилось, теорема 1 позволяет утверждать, что через каждую точку открытой области G, где функция у = непрерывна вместе с производной , проходит решение у = задачи Коши

y'= f(x, у) , y(х_о)=y_0,

определенное в некоторой окрестности точки х₀, именно при (число h определяется размерами прямоугольной окрестности ). Это решение «натыкается» на границу прямоугольника П и через эту границу «переходит» из П в G\П. Поставим перед собой задачу проследить поведение интегральной кривой, соответствующей найденному локальному решению, вне П.

Теорема 3 (существование и един­ственность непродолжимого решения задачи Коши.)

Пусть функция f (x, у) определена и непрерывна в открытой области G и обладает там непрерывной производной (т. е. ). Тогда:

а) Какова бы ни была точка , задача Коши

y'=f(x, у), (16.1)

у(х_о)=y₀, (16.2)

имеет непродолжимое решение y=F(x), определенное в некотором (максимальном) интервале , содержащем точку х₀. При стремлении х к крайним точкам этого интервала (т. е. при или ) соответствующая точка M (x, F(х)) интегральней кривой стремится к границе области.

б) Решение F(х) единственно в том смысле, что любое другое решение ψ(x) уравнения (16.1),. удовлетворяющее тому же начальному условию (16.2), совпадает с F(х) в промежутке (a, b) своего определения (причем ).

Замечание . Стремление точки М (х, F(х)) при (или ) к границе следует понимать в том смысле, что точка М «покидает» любую строго внутреннюю ограниченную подобласть G' области G . При этом, как мы увидим, могут представиться следующие случаи:

а) Точка М «уходит» в бесконечность (т. е. по крайней мере одна из ее координат стремится к ∞ или -∞).

б) Точка М приближается к промежутку (с, d), расположенному на некоторой вертикальной прямой х=const, подходя как угодно близко к любой точке этого промежутка. При этом, конечно, указанный промежуток х=const, является частью .

в) Точка М неограниченно приближается к фиксированной точке .

Учитывая сказанное, мы будем употреблять такое наглядное описание поведения непродолжимого решения: «интегральная кривая y=F(x) проходит от границы и до границы области G».

Основная идея доказательства — продол­жение локального решения — очень проста. Точку мы погружаем в замкнутый куб П_о, целиком принадлежащий обла­сти G, и, применяя терему Коши-Пикара, получаем «кусок» искомой инте­гральной кривой вблизи «начальной» точки . На этой кривой берем самую правую точку , и для нее проделываем ту же процедуру и т. д. Таким образом, мы на каждом шаге продолжаем решение вправо. Такой процесс даст непродолжимое решение задачи.

По теореме существования и единственности существует ре­шение у=φ(х) задачи (16.1), (16.2), определенное в проме­жутке , где . Обозначим

Теперь повторим про­веденное построение, беря вместо точки точку . По теореме существования и единственности существует решение уравнения (16.1), проходящее через точку , определённое в промежутке

(где ).

В пере­сечении отрезков , решения и совпадают в силу свойства единственности (локального) решения. Таким образом, функция

является решением задачи (16.1), (16.2) в промежутке , . Продолжая аналогично дальше, мы получим на n-м шаге решение F_n(x) задачи Коши (16.1), (16.2), определенное в промежутке . При придем, таким образом, к решению F(x), определенному в промежутке ), где

Итак, покидая любую строго внутреннюю подобласть, интеграль­ная кривая приближается сколь угодно близко к границе.

Аналогично проводится продолжение локального решения влево. Полученное непродолжимое решение F(х) будет, таким образом, определено в некотором максимальном интервале .

Единственность найденного решения следует по существу из того соображения, что переход от F_n к F_n+1 однозначен (в силу единственности локального решения). Придадим этому соображению точную форму в нижеследующей теореме.

Теорема 4. (единственности). Пусть функция f(x, у) непрерывна в открытой области G вместе с производной , и пусть F(х) — непродолжаемое решение задачи Коши

y' = f (x,y), (16.3)

(16.4)

с областью определения . Если — другое решение за­дачи (16.3), (16.4) с областью определения (а, b), то есть сужение F(x), т. е. и при .

Пример 1. Рассмотрим уравнение

(16.5)

Здесь , т. е. правая часть определена на всей плоско­сти (и имеет квадратичный рост по у). Условия теоремы Коши-Пикара выполнены при любых начальных данных (х₀,у₀), как бы ни был выбран исходный прямоугольник П. Казалось бы, нет видимых препятствий для неограниченного продолжения соответствующего решения вправо и влево. Однако это не так. Пусть для опреде­ленности х_о=0, у_о= b ≠ 0.

Из (16.5) получаем при у ≠ 0

(16.6)

Мы потеряли при этом решение которое не содержится в формуле (16.6) ни при каком значении С. Это решение соответствует начальному условию х_о=0, у_о=b=0. Любопытно отметить, что общее решение уравнения (16.5), как совокупность частных решений, должно записываться в виде

Для искомого частного решения при b > 0 получаем выражение

(16.7)

Таким образом, максимальный интервал определения решения поставленной задачи Коши отличается от всей прямой и зависит от начальных значений. Отметим еще, что при приближении х к концам интервала решение «уходит» в бесконечность.

ЗАКЛЮЧЕНИЕ

В пособии рассмотрены только основные методы интегрирования обыкновенных дифференциальных уравнений первого порядка. Навыки интегрирования, приобретенные при работе с данным пособием, помогут читателям успешно справиться и с исследованием различных конкретных дифференциальных моделей, возникающих в практических задачах.

В настоящее время на практике широко используются и приближенные методы интегрирования, которые не рассматривались в данном пособии, читатель может с ними познакомиться в учебной литературе (4,7,8).

Библиографический список

1.Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М.:" Наука", 1970

2.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.:" Наука", 1970.

3.Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.:" Наука", 1992.