11. Интегрирующий множитель
В тех случаях, когда левая часть уравнения
М(х,у)dх + N(x,y)dy = 0 ( 11.1)
не является полным дифференциалом, удаётся подобрать функцию (x, y), после умножения, на которую левая часть (6) превращается в полный дифференциал
Такая функция (x, y) называется интегрирующим множителем. Из определения интегрирующего множителя имеем
или
,
откуда
.
(11.2)
Мы получили для нахождения интегрирующего множителя уравнение в частных производных.
Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (11.2), т. е. найти интегрирующий множитель.
1.Пусть
=(x).
Тогда
и
уравнение (11.1) примет вид
.
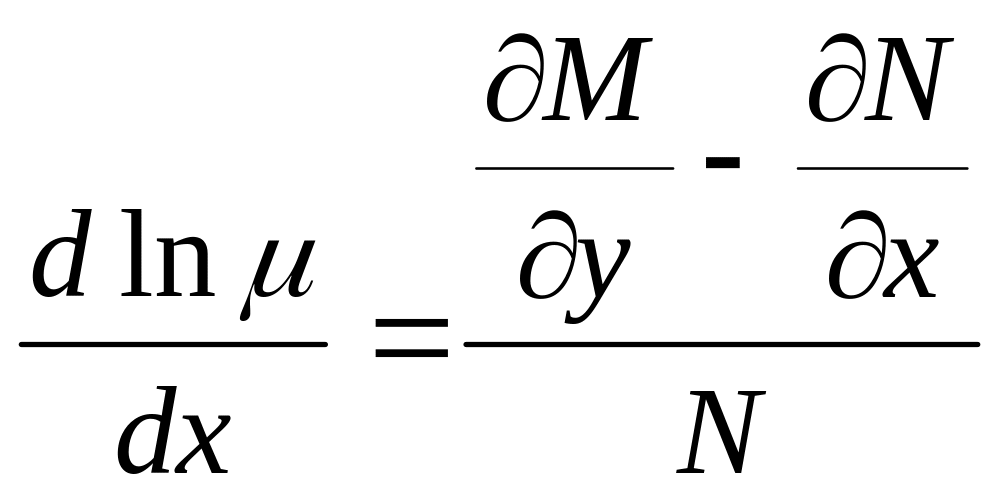(11.3)
Для существования интегрирующего множителя, не зависящего от y, необходимо и достаточно, чтобы правая часть ( 11.3) была функцией только от x. В таком случае ln найдётся интегрированием по х.
Пример 1. Рассмотрим уравнение
(x + y2) dx – 2xy dy = 0.
Решение. Здесь M=x+y2, N= - 2xy.
Имеем
.
Следовательно,
,
,
.
После умножения на ( x) уравнение
становится уравнением в полных дифференциалах. Его левую часть можно представить в виде
.
Откуда
и общий интеграл данного
уравнения есть
.
2.
Рассмотрим случай =(у).
Если
есть функция, зависящая только от y,
тогда уравнение (5) имеет интегрирующий
множитель =(y),
зависящий только от у.
Пример 1. Найти общий интеграл уравнения
Решение:
Здесь M=
, N=
Так как условие
не выполняется, отыскиваем интегрирующий множитель. Рассмотрим соотношение
.
Оно зависит только от у, поэтому интегрирующий множитель будет иметь вид
,
откуда
.
После
умножения на
и
решения уравнения в полных дифференциалах
получаем общий интеграл уравнения
12.Уравнения, неразрешенные относительно производной
1. Уравнения, не содержащие явно одного из переменных.
Отыскание решений уравнений вида
F ( х, у, у ) = 0 (12.1)
вызывает
особые трудности. Например,
уравнение
вообще не имеет действительных решений.
Общего метода решения уравнений,
неразрешимых относительно производной,
нет. Рассмотрим некоторые случаи, при
которых уравнение (1) имеет решение.
1. Пусть уравнение (12.1) удается разрешить относительно производной, тогда (12.1) распадается на уравнения вида
(12.2)
которые
могут быть проинтегрированы вышеизложенными
методами. Пусть каждое из уравнений
(14.2) имеет общее решение
.
Совокупность общих решений уравнений
(12.2) называется общим
решением уравнения
(12.1).
Например,
уравнение
имеет общее решение
.
Пример 1. Найти общий интеграл уравнения:
Решение. Разлагая левую часть уравнения на множители, получим:
,
откуда
и
.
Оба эти уравнения являются уравнениями
с разделяющимися переменными. Их общие
интегралы:
,
.
Поэтому общий интеграл исходного уравнения имеет вид
2. Пусть уравнение (14.1) имеет вид F(у) = 0, причем существует хотя бы один действительный корень
,
(12.3)
т.к.
уравнение не содержит х
,у то
-
постоянные. Тогда
интегрируя (12.3) получаем
,
а уравнение
дает общий интеграл исходного
уравнения.
Пример 2. Найти общий интеграл уравнения:
Решение. Общий интеграл данного уравнения имеет вид
.
3. Пусть уравнение (14.1) не содержит независимой переменной
F ( у , у¢ ) = 0 (12.4)
и трудно разрешимо относительно производной, тогда целесообразно ввести параметр и заменить уравнение (12.4) двумя
,
такими,
что
.
Так как
то
,
откуда интегрируя, находим х.
Пример 3. Найти общее решение уравнения
.
Решение.
Положим
;
тогда
.
Из
равенства
находим
.
Та как
,
то
и
.
В параметрической форме общее решение
запишется так:
Исключим параметр p. Для этого из первого уравнения находим t и подставляем во второе. Имеем
и
.
4. Пусть уравнение (14.1) не содержит у , т.е. имеет вид
F(х,у¢) = 0 (12.5)
и трудно разрешимо относительно производной, тогда как и ранее, вводят параметр и заменяют уравнение (12.5) двумя
,
такими,
что
.
Так как
то
Пример 4. Найти общее решение уравнения
.
Решение.
Положим
.
Из равенства
находим х
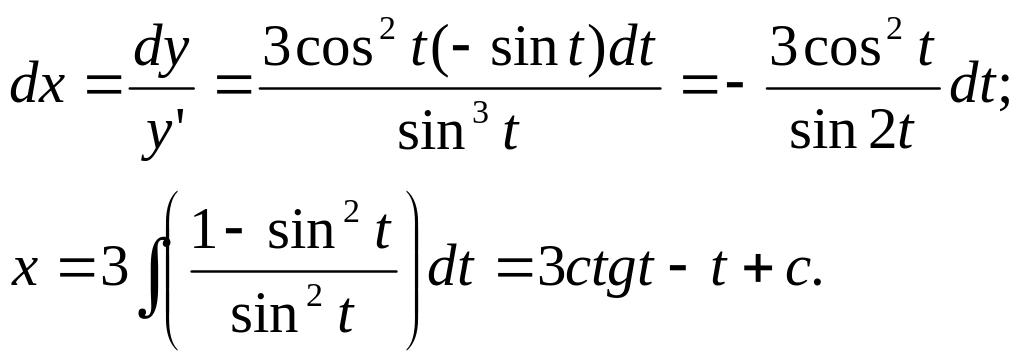
Общее решение уравнения получаем в параметрической форме.
5. Если дифференциальное уравнение F(х,у,у) = 0 разрешимо либо относительно искомой функции
у = f(x.y'), либо относительно аргумента х = f(y,y), то оно может быть проинтегрировано путем введения параметра р = у'. Исходное уравнение перейдет в алгебраическое. Дифференцируя соответственно по х или по у, получим системы уравнений
или 
решения которых находятся в явном или параметрическом виде.
Пример 5: Найти общее решение уравнения
в параметрической форме.
Решение.
Положим
,
тогда
.
Равенство
перепишем
в форме
,
так как
то
.
Общее решение запишется в следующем виде:
Пример 6: Найти общее решение уравнения
Решение. Так как уравнение разрешимо относительно у
,
то вводя параметр найдем выражение для х :
Исключая
параметр р,
находим
общее решение
.