
- •Оглавление
- •Введение
- •Глава 1. Обобщенная структурная схема и основные подсистемы радиотехнических систем передачи информации (рспи)
- •Глава 2. Определение и классификация различных видов модуляции
- •Глава 3. Амплитудная модуляция
- •3.1. Математическое выражение модулированных колебаний
- •3.2. Анализ модулированных колебаний
- •3.3. Методы формирования однополосного сигнала
- •3.4. Балансные модуляторы
- •3.5. Полосовые фильтры
- •Глава 4. Угловая модуляция
- •4.1 Фазовая модуляция (фм)
- •4.2. Частотная модуляция (чм)
- •4.3. Общие соображения о спектре сигналов с угловой модуляцией
- •4.4 Спектральное разложение чм и фм сигналов при малых индексах модуляции
- •4.5. Спектр сигнала с угловой модуляцией при произвольном значении индекса модуляции
- •4.6. Частотная модуляция (чм) в автогенераторе
- •Глава 5. Радиоприемные устройства
- •5.1. Общие сведения
- •5.2. Основные узлы радиоприемников и их характеристики
- •5.3. Ручные и автоматические регулировки в радиоприемниках
- •Заключение
- •394026 Воронеж, Московский просп., 14
Глава 4. Угловая модуляция
4.1 Фазовая модуляция (фм)
Если полная фаза
процесса
![]() ,
где
,
где
![]() – сообщение,
– сообщение,
![]() – коэффициент пропорциональности,
– коэффициент пропорциональности,
![]() – значение частоты в
– значение частоты в
![]() отсутствии сообщения
,
то имеем сигнал с фазовой модуляцией
отсутствии сообщения
,
то имеем сигнал с фазовой модуляцией
![]() .
Если сообщение
.
Если сообщение
![]() то ФМ – сигнал является простым
высокочастотным сигналом.
то ФМ – сигнал является простым
высокочастотным сигналом.
Если
![]() ,
то с увеличением значений ФМ сообщения
полная фаза
,
то с увеличением значений ФМ сообщения
полная фаза
![]() растет во времени быстрее, чем по
линейному закону. При уменьшении
модулирующего сообщения происходит
спад скорости роста
растет во времени быстрее, чем по
линейному закону. При уменьшении
модулирующего сообщения происходит
спад скорости роста
![]() во времени см. (рис. 4.1).
во времени см. (рис. 4.1).
Р ис.
4.1 Фазовая модуляция
ис.
4.1 Фазовая модуляция
В моменты времени,
когда сигнал
достигает экстремальных значений,
абсолютный угол между ФМ – сигналом и
немодулированным гармоническим
колебанием оказывается наибольшим.
Предельное значение этого фазового
сдвига называют девиацией фазы
![]() .
В общем случае, когда сообщение
изменяет знак, принято различать девиацию
фазы вверх
.
В общем случае, когда сообщение
изменяет знак, принято различать девиацию
фазы вверх
![]() и девиацию фазы вниз
и девиацию фазы вниз
![]() .
.
4.2. Частотная модуляция (чм)
Мгновенная частота
![]() сигнала с угловой модуляцией определяется
как первая производная от полной фазы
по времени, т.е. мгновенная частота –
это скорость изменения полной фазы:
сигнала с угловой модуляцией определяется
как первая производная от полной фазы
по времени, т.е. мгновенная частота –
это скорость изменения полной фазы:
![]() – мгновенная частота.
– мгновенная частота.
Откуда, полная фаза равна:
![]()
где
![]() – начальная фаза в момент времени
– начальная фаза в момент времени
![]() .,
.,
При ЧМ – сигнале между сообщением и мгновенной частотой будет связь вида
![]() .
.
Поэтому
![]() ,
,

В соответствии с
этим параметрами ЧМ — сигнала являются
девиация частоты вверх
![]() и девиация частоты вниз
и девиация частоты вниз
![]() .
Если
.
Если
![]() - достаточно гладкая функция, то внешне
осциллограммы ФМ и ЧМ — сигналов не
отличаются (рис. 4.2).
- достаточно гладкая функция, то внешне
осциллограммы ФМ и ЧМ — сигналов не
отличаются (рис. 4.2).
Р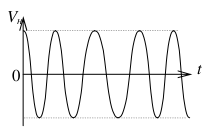 ис.
4.2 Частотная модуляция
ис.
4.2 Частотная модуляция
Однако имеет место принципиальная разница: фазовый сдвиг между ФМ - сигналом и немодулированным пропорционален , для ЧМ этот сдвиг пропорционален интегралу от . То есть ЧМ и ФМ - сигналы ведут себя по-разному при изменении частоты модуляции и амплитуды модулирующего колебания.
При ЧМ девиация
частоты
![]() (амплитуде
НЧ – сигнала), в то же время девиация
частоты
(амплитуде
НЧ – сигнала), в то же время девиация
частоты
![]() не зависит от частоты
модулирующего сигнала.
не зависит от частоты
модулирующего сигнала.
Р ис.
4.3 Зависимости девиации частоты и индекса
угловой модуляции при ЧМ и ФМ
ис.
4.3 Зависимости девиации частоты и индекса
угловой модуляции при ЧМ и ФМ
При ФМ индекс
модуляции
![]() – амплитуде НЧ - сигнала независимо от
частоты модуляции. Как следствие этого,
девиация частоты при фазовой модуляции
линейно увеличивается с ростом частоты
модулирующего сигнала (рис. 4.3).
– амплитуде НЧ - сигнала независимо от
частоты модуляции. Как следствие этого,
девиация частоты при фазовой модуляции
линейно увеличивается с ростом частоты
модулирующего сигнала (рис. 4.3).
Таким образом, при гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции.
4.3. Общие соображения о спектре сигналов с угловой модуляцией
Если колебание
![]() получено с помощью ФМ, то
получено с помощью ФМ, то
![]() и
полностью совпадают по форме и отличаются
лишь постоянными коэффициентами. При
этом очевидно, с точностью до постоянного
коэффициента совпадают спектры функций
и
полностью совпадают по форме и отличаются
лишь постоянными коэффициентами. При
этом очевидно, с точностью до постоянного
коэффициента совпадают спектры функций
![]() и
.
При ЧМ функция
является интегралом от передаваемого
сообщения
т.к. интегрирование является линейным
преобразованием, то при ЧМ спектр функции
состоит из тех же компонент, что и спектр
сообщения
,
но с измененными амплитудами и фазами.
Отвлекаясь от способа осуществления
угловой модуляции и считая заданным
спектр функции
находим спектр модулированного колебания
и
.
При ЧМ функция
является интегралом от передаваемого
сообщения
т.к. интегрирование является линейным
преобразованием, то при ЧМ спектр функции
состоит из тех же компонент, что и спектр
сообщения
,
но с измененными амплитудами и фазами.
Отвлекаясь от способа осуществления
угловой модуляции и считая заданным
спектр функции
находим спектр модулированного колебания
![]() Для этого выражение для
преобразуем к виду:
Для этого выражение для
преобразуем к виду:
![]() .
.
Из этого выражения
следует, что модулированное по углу
колебание можно рассматривать как сумму
двух квадратурных колебаний: косинусного
![]() и синусного
и синусного
![]() ,
каждое из которых модулировано только
по амплитуде. Закон АМ для косинусного
колебания определяется медленной
функцией
,
каждое из которых модулировано только
по амплитуде. Закон АМ для косинусного
колебания определяется медленной
функцией
![]() ,
для синусного – функцией
,
для синусного – функцией
![]() .
Но для определения спектра АМ колебания
достаточно сдвинуть на частоту
спектр огибающей амплитуд. Следовательно,
для нахождения спектра колебания
необходимо найти сначала спектры функций
и
,
т.е. спектры огибающих квадратурных
колебаний. Из приведенных рассуждений
следует, что при одном и том же передаваемом
сообщении спектр колебания, модулированного
по углу, значительно сложнее, чем спектр
модулированного по амплитуде.
Действительно, т.к.
и
являются нелинейными функциями своего
аргумента
,
то спектры этих колебаний могут
существенно отличаться от спектра
функции
.
.
Но для определения спектра АМ колебания
достаточно сдвинуть на частоту
спектр огибающей амплитуд. Следовательно,
для нахождения спектра колебания
необходимо найти сначала спектры функций
и
,
т.е. спектры огибающих квадратурных
колебаний. Из приведенных рассуждений
следует, что при одном и том же передаваемом
сообщении спектр колебания, модулированного
по углу, значительно сложнее, чем спектр
модулированного по амплитуде.
Действительно, т.к.
и
являются нелинейными функциями своего
аргумента
,
то спектры этих колебаний могут
существенно отличаться от спектра
функции
.
Это обстоятельство, а также наличие двух квадратурных слагаемых, показывает, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра колебания на величину несущей частоты , как это имеет место при АМ.
