Задача №3
Сделать чертеж и составить уравнение линий:
1)
каждая точка которой равноудалена от
точки
и от оси
;
2)
каждая точка которой находится втрое
дальше от точки
,
чем от точки
;
3)
получаемой при движении точки
в плоскости так, что ее расстояние от
точки
остается вдвое меньше расстояния от
прямой
;
4)
для каждой точки которой расстояние
от начала координат и от точки
относятся друг к другу как
;
5)
получаемой при движении точки
в плоскости так, что ее расстояние от
прямой
вдвое меньше расстояния от точки
;
6)
каждая точка которой равноудалена от
точки
и от прямой
;
7)
для каждой точки которой расстояние
от точки
и от прямой
относятся как
;
8)
расстояние каждой точки которой от
точки
втрое больше расстояния от точки
;
9)
каждая точка которой равноудалена от
точки
и от прямой
;
10)
каждая точка которой одинаково удалена
от точки
и от прямой
;
11)
полученной при таком движении точки
,
что расстояние от нее до точки
вдвое меньше расстояния от точки
;
12)
расстояние каждой точки которой от
точки
и от прямой
относятся как
;
13)
каждая точка которой находится вдвое
дальше от точки
,
чем от точки
;
14)
для каждой точки которой сумма квадратов
расстояний до точек
и
равна
;
15)
каждая точка которой отстоит от точки
втрое дальше, чем от начала координат;
16)
для каждой точки которой сумма квадратов
расстояний до сторон квадрата с вершинами
,
,
,
есть величина постоянная, равная
;
17)
для каждой точки которой отношение
расстояния до точки
к расстоянию до прямой
равно
;
18)
каждая точка которой одинакова удалена
от точки
и от начала координат;
19)
для каждой точки которой сумма квадратов
расстояний до точек
и
равна
;
20)
каждая точка которой одинаково удалена
от точки
и от оси
.
Задача №4
Линия задана
уравнением
в полярной системе координат. Требуется:
1) построить линию по точкам от
до
,
придавая значения
через промежуток
;
2) найти уравнение линии в декартовой
системе координат, у которой начало
совпадает с полюсом, а положительная
полуось
-
с полярной осью; 3) определить вид линии
по ее уравнению в декартовой системе
координат; 4) сделать чертеж.
1.
;
2.
;
3.
;
4.
;
5.
;
6.
;
7.
;
8.
;
9.
;
10.
;
11.
;
12.
;
13.
;
14.
;
15.
;
16.
;
17.
;
18.
;
19.
;
20.
;
Задача №5
Решить систему линейных уравнений двумя способами:
1) методом Крамера;
2) используя обратную матрицу.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Задача №6
Решить систему линейных уравнений методом Гаусса.
1.
2.
3.
4.
5.
6.
7.
8.
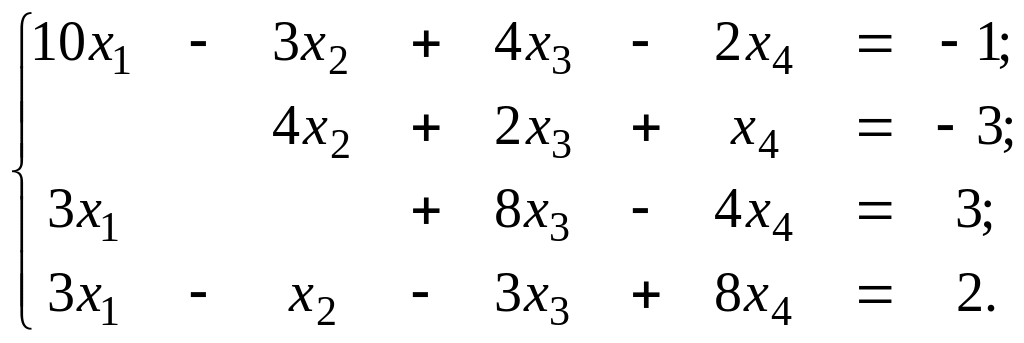
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Задача №7
Исследовать кривую второго порядка и построить ее график.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача №1
Даны
координаты вершин треугольника
:
,
,
.
Найти:
уравнения сторон и и их угловые
коэффициенты;
угол в радианах (градусах) с точностью до двух знаков после запятой;
уравнение высоты и ее длину;
уравнение медианы и координаты точки пересечения этой медианы с высотой .
Сделать
чертеж (рис.1).
Рис. 1
Решение.
1) Найдем координаты векторов
и
,
для чего воспользуемся формулой
.
Тогда
,
.
Эти векторы являются направляющими
векторами прямых, на которых лежат
соответствующие стороны треугольника
и для получения их уравнений можно
использовать каноническое уравнение
прямой на плоскости
.
В результате получим
(
),
(
).
Разрешая эти
уравнения относительно
,
т.е. приводя их к виду уравнения прямой
с угловым коэффициентом
,
найдем
,
.
2) Угол
треугольника совпадает с углом между
векторами
и
и для его нахождения можно использовать
формулу
,
По
таблице найдем значение угла
:
<
(
).
3) Для получения уравнения высоты приведем уравнение стороны к виду общего уравнения прямой на плоскости
(
).
Из рисунка видно,
что вектор нормали к прямой
является направляющим вектором высоты
,
т.е.
,
и можно вновь воспользоваться каноническим
уравнением прямой на плоскости
(
).
Длину высоты
вычислим по формуле вычисления расстояния
от точки
до прямой
:
.
В нашем случае
.
4) Найдем координаты
точки
,
являющейся серединой отрезка
;
.
Т.о.,
,
и для нахождения уравнения медианы
можно использовать уравнение прямой,
проходящей через две точки
и
:
.
Тогда получим
или
(
).
Наконец, для вычисления координат точки , решим совместно уравнения прямых и , предварительно приведя их уравнения к общему виду
.
Отсюда получим
.