Решение линейных неоднородных уравнений с постоянными коэффициентами с правой частью специального вида методом подбора частного решения или методом неопределенных коэффициентов
Пусть требуется найти общее решение неоднородного линейного уравнения п-го порядка с постоянными коэффициентами
(22)
Его решение представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
При некоторых специальных видах неоднородности это частное решение можно подобрать по известной схеме.
1) Если
где Рп (х) – многочлен
степени п, то частное решение
уравнения (22)
,
(23)
если число k не является корнем характеристического уравнения, или
, (24)
если k – корень характеристического уравнения кратности s. Коэффициенты А0, А1,…, Ап можно найти методом неопределенных коэффициентов, подставив уч.н. и его производные нужных порядков в уравнение (22).
2) При
,
если числа a±bi
не являются корнями характеристического
уравнения, частное решение имеет вид:
,
(25)
где
многочлены с неопределенными коэффициентами
одной и той же степени l
= max(m,
n).
Если же a±bi – корни характеристического уравнения кратности s,
. (26)
Если правая часть уравнения (22) представляет собой сумму функций, для каждой из которых можно подбором найти частное решение:
то частное решение такого уравнения
является суммой частных решений уравнений
и
Пример 19. Найти общее решение
уравнения
Решение. Найдем общее решение
однородного уравнения
Характеристическое уравнение
имеет корни 0 (кратности 1) и 1 (кратности
2). Следовательно,
Перейдем к поиску частного решения. Поскольку число 1 – коэффициент при х в показателе степени правой части уравнения – является корнем характеристического уравнения кратности 2, ищем уч.н. в виде (24) при s = 2, n = 0: yч.н.=Ax2ex. Тогда
Подставим полученные выражения в
исходное неоднородное уравнение:
Следовательно, общее решение исходного уравнения имеет вид:
Пример 20. Найти общее решение
уравнения
Решение. Характеристическое
уравнение:
Общее решение однородного уравнения:
.
Найдем частное решение, соответствующее
неоднородности f1(x)
= 3x. Так как λ = 0 –
корень характеристического уравнения,
частное решение имеет вид (24): yч.н.1
= x (Ax
+ B) = = Ax2
+ Bx. Поскольку
при подстановке в уравнение получаем:
2A – 2Ax
– B = 3x,
откуда 2A – B
= 0, - 2A = 3. Решая полученную
систему, находим:
Для f2(x) = sin 2x yч.н.2 задаем по формуле (25) при a = 0, b = 2, l = 0:
yч.н.2
= A sin2x
+ B cos2x,
Подставим в уравнение:
Отсюда В = 0,1, А = - 0,2,
уч.н.2 = - 0,2 sin2x + 0,1 cos2x.
Таким образом, найдено общее решение исходного уравнения:
Задания для самоконтроля:
Определить вид частного решения.
1.
.
Ответ:
.
2.
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
.
Решить уравнения.
5.
.
Ответ:
.
6.
.
Ответ:
.
7.
.
Ответ:
.
8.
.
Ответ:
.
Решение неоднородного линейного уравнения с постоянными коэффициентами методом вариации постоянных (метод Лагранжа)
Если неоднородность в правой части уравнения (22) не позволяет использовать формулы (23)-(26) для подбора частного решения, можно воспользоваться методом вариации постоянных или методом Лагранжа.
Пусть решение однородного уравнения
второго порядка с постоянными
коэффициентами (18) записано в виде: уо.о.
= С1у1 + С2у2,
где у1, у2 –
фундаментальная система решений. Будем
считать, что при этом решение неоднородного
уравнения
имеет вид:
.
Функции С1(х) и С2(х)
можно определить из системы уравнений
для их производных:
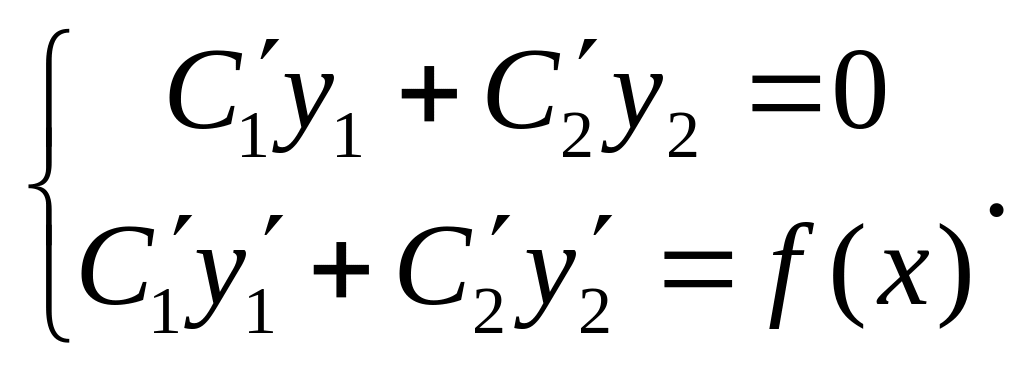(27)
Пример 21. Найти общее решение
уравнения
Решение. Решим однородное уравнение: λ2 + 64 = 0, λ = ± 8i, yо.о = С1cos 8x + C2sin 8x,
y = С1 (х) cos 8x + C2 (х) sin 8x. Составим вариационную систему:
Получена линейная система для С1’ и С2’. Для ее решения умножим первое уравнение на 8sin 8x, а второе – на cos 8x и сложим левые и правые части полученных равенств:
где
Теперь исключим из системы С2’. Для этого умножим первое уравнение на 8 cos 8x, а второе – на
–sin 8x:
Ĉ = const. Итак, общее решение исходного уравнения:
Задания для самоконтроля: Решить уравнения.
1.
.
Ответ:
.
2.
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
,
или
.