2. Однородные уравнения
Уравнение, которое можно записать в форме
(5)
называется однородным дифференциальным
уравнением. Оно тоже может быть сведено
к уравнению с разделяющимися переменными
для функции
.
При этом
и уравнение для t
примет вид:
уравнение с разделяющимися переменными.
Пример 6. Найти общий интеграл
уравнения
.
Решение. Разделим обе части равенства на х:
и сделаем замену:
.
Тогда
общий интеграл уравнения.
Пример 7. Найти общий интеграл уравнения y² + x²y′ = xyy′.
Решение. Преобразуем уравнение: y′(xy – x²) = y²,
,
.
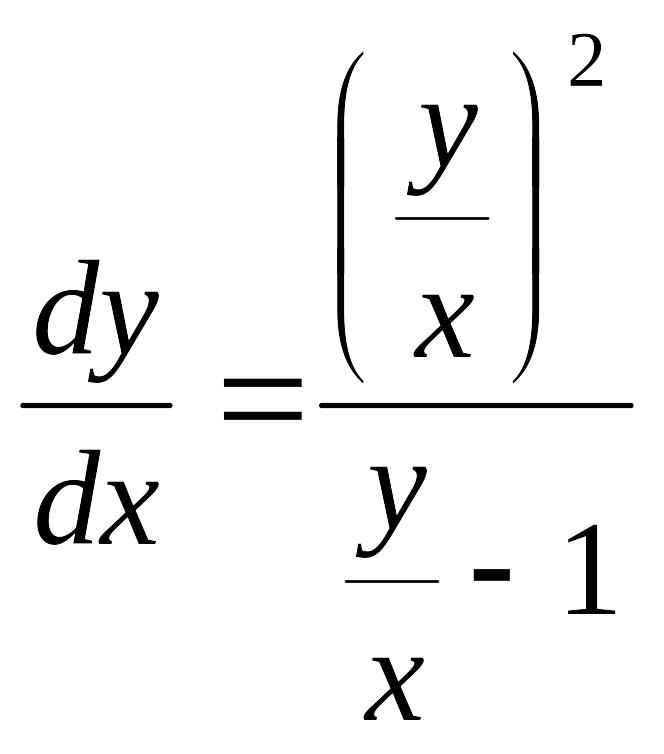После замены y = x t получим:
,
t – ln | t | = ln | x | + ln |C|
,
,
.
К однородному уравнению, в свою очередь, можно привести уравнение вида
(6)
при условии
.
При этом производится параллельный
перенос в плоскости (х, у) такой,
чтобы начало координат совместилось с
точкой (x0; y0)
пересечения прямых ax
+ by + c
= 0 и a1x
+ b1y
+ c1 = 0. Тогда
в новых координатах
уравнение будет выглядеть так:
,
или
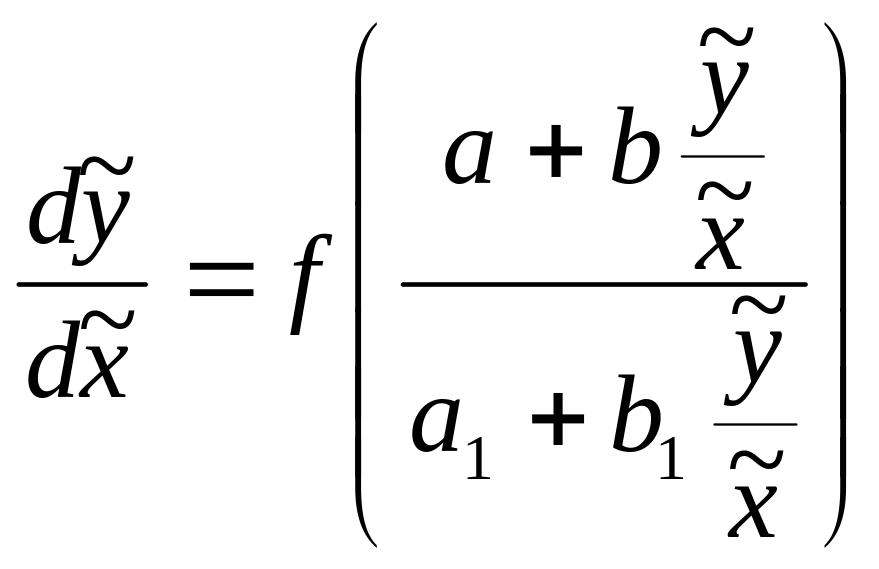- однородное уравнение.
Пример 8. Найти общее решение уравнения
.
Решение.
Решим систему уравнений
.
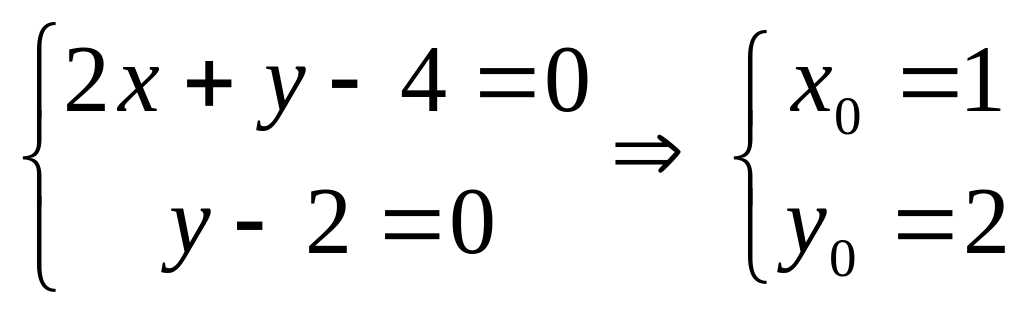Тогда
,
и в новых переменных (с учетом того, что
)
получаем уравнение
.
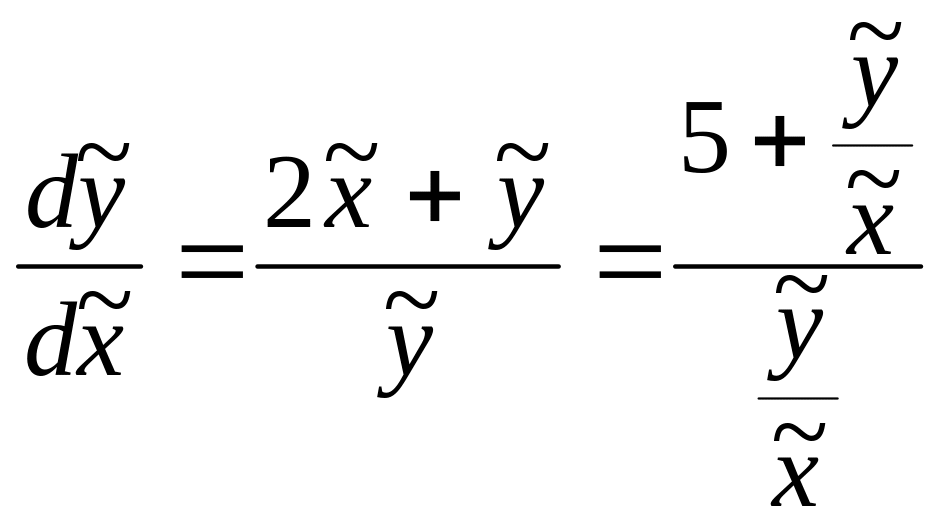Замена
приводит к уравнению
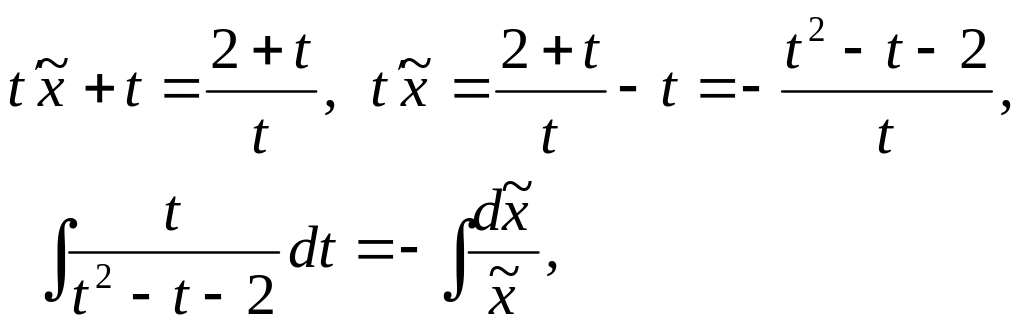
После упрощения и обратной замены получаем общее решение в виде:
.
Задания для самоконтроля: Решить уравнения
1.
.
Ответ:
.
2.
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
.
3. Уравнения в полных дифференциалах (ознакомительно)
Если в дифференциальном уравнении
(7)
функции М (х, у) и N
(x, y)
удовлетворяют условию
такое уравнение называется уравнением
в полных дифференциалах. Смысл названия
объясняется тем, что при этом существует
функция U (x,
y) такая, что
Тогда из уравнения (7) следует, что
,
что является общим интегралом исходного
уравнения. Таким образом, задача сводится
к отысканию функции U.
Ее можно найти в виде:
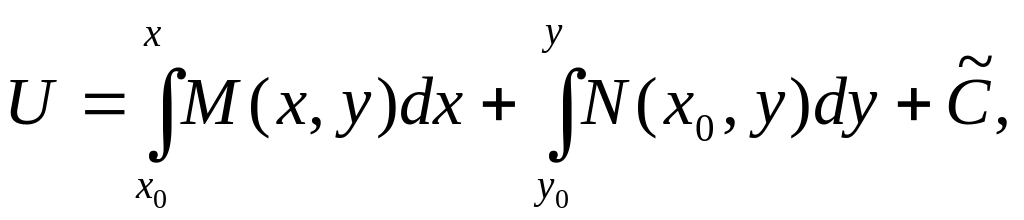
где х0, у0 – любые
числа, входящие в область определения
функций М и N, а
- произвольная постоянная.
Пример 9. Решить задачу Коши для
уравнения
,
если у(1) = 1.
Решение. Проверим, действительно
ли перед нами уравнение в полных
дифференциалах:
условие выполнено. Для поиска U
(x, y)
зададим х0 = у0 = 0,
тогда
При х = у =1 найдем С из равенства
ех + ху – еу
= С: е + 1 – е = С, С = 1.
Следовательно, искомое частное решение
имеет вид: ех + ху – еу
= 1.
4. Линейные уравнения первого порядка
Уравнение вида
(8)
называется линейным неоднородным уравнением первого порядка, поскольку искомая функция и ее производная входят в него в виде линейной комбинации. Если b (x) ≡ 0, уравнение является однородным, причем однородное линейное уравнение – это уравнение с разделяющимися переменными.
Существует два способа решения неоднородных линейных дифференциальных уравнений первого порядка.
Первый способ - метод вариации постоянной.
Сначала ищется решение соответствующего линейного уравнения при нулевой правой части:
.
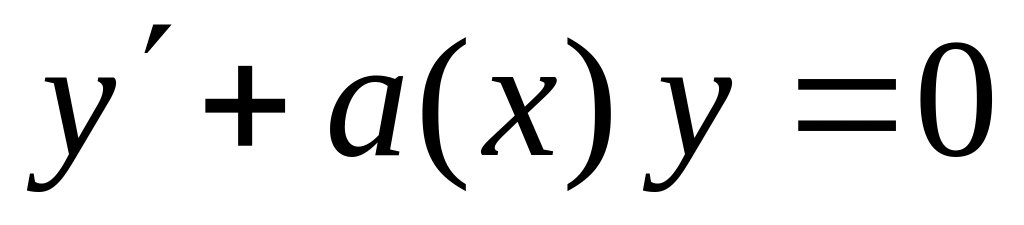Разделяя в нем переменные, получим его
общее решение в виде
Получив решение однородного уравнения
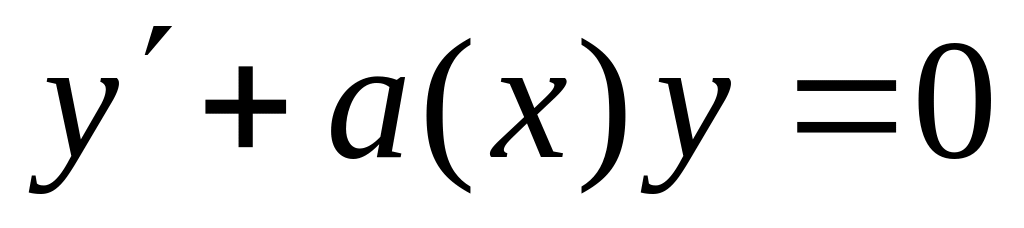в виде y = f
(x, C),
считают, что решение уравнения (8) имеет
такой же вид, но С = С (х) – не
постоянная, а функция от х, вид
которой можно определить, подставив y
= f (x,
C (х)) в уравнение.
Т.е
подставляем в (8) и получаем дифференциальное
уравнение с разделяющимися переменными
относительно функции С(x), интегрируя
которое находим эту функцию. В результате
общее решение уравнения (8) может быть
представлено в виде
(9)
Формула (9) является общим решением линейного дифференциального уравнения (8) в форме Коши.
Пример 10. Найти общее решение
уравнения
Решение.
Решим однородное уравнение:
Теперь
будем искать решение неоднородного
уравнения в виде:
у = С (х)∙е-2х.
.
Подставим y и y’ в исходное уравнение:
,
где
-
произвольная постоянная. Следовательно,
общее решение неоднородного уравнения:
Пример 11. Найти общее решение уравнения у′ = 2 х (х² + y).
Решение. Представим уравнение в виде:
y′ - 2xy = 2x³
и решим соответствующее однородное уравнение:
y′ - 2xy = 0.
Применим
метод вариации постоянных: пусть решение
неоднородного уравнения имеет вид:
,
тогда
.
Подставим полученные
выражения в уравнение:
.
Следовательно,
,
При этом общее решение
исходного уравнения
.
Второй способ – метод Бернулли.
Решение линейного дифференциального уравнения (8) может быть также получено, если искомую функцию представить в виде произведения двух произвольных функций:
.
Тогда
Подставляя
и
в (8), получим
Функцию u(x) подбираем так, чтобы она была одним из решений уравнения
.
После разделения переменных получим
Тогда уравнение (8) примет вид
.
Следовательно,
Интегрируя это уравнение, находим функцию v:
.
Подставляя
и v в
,
получим общее решение уравнения (8) в
виде (9).
К линейному можно привести и уравнение вида
(10)
называемое уравнением Бернулли.
Уравнение Бернулли является нелинейным,
но оно приводится к линейному следующим
преобразованием. Для этого вводится
новая функция
,
для которой
.
Разделим обе части уравнения (10) на уп:
или
получили линейное уравнение относительно
z.
Пример 12. Найти общий интеграл
уравнения
.
Решение.
Разделим обе части равенства на у2:
и сделаем замену:
.
Решим уравнение для z
методом вариации произвольной постоянной:
.
Однородное уравнение:
.
Подставим полученные выражения в неоднородное уравнение:
Пример 13. Решить уравнение
Решение.
Умножаем
обе части уравнения на
Вводим
замену
и уравнение преобразуется в линейное
Находим сначала решение соответствующего линейного однородного уравнения
Решение неоднородного уравнения отыскиваем в виде
тогда
После интегрирования получим
поэтому общее решение исходного уравнения будет иметь вид
Задания для самоконтроля: Решить уравнения
1.
.
Ответ:
.
2.
.
Ответ:
.
3.
.
Ответ:
.
4.
.
Ответ:
.