1. Цель расчетно - графических заданий
Расчетные задания являются основным этапом изучения дисциплины «Механика» и выполняются с целью:
- расширения и закрепления знаний по изучаемой дисциплине;
- приобретения навыков использования теоретических знаний для решения конкретных технических задач;
- приобретения навыков самостоятельной инженерной работы и принятия решений;
- выработки навыков оформления технической документации: составления расчетно-пояснительной записки и разработки графического материала, иллюстрирующего расчеты.
2. Выбор варианта задания
Информация для выполнения РГЗ определяется вариантом задания – тремя последними номера N зачетной книжки студента и соответствующей таблицей 9 исходных данных в методических указаниях [3].
Пусть K, L и M - три последних цифры номера N, перечисленные в порядке слева направо. Пусть например, зачётная книжка имеет номер 10195. Тогда K= 1, L= 9, M= 5.
Более подробные дополнительные инструкции по выбору исходной информации к задаче могут быть приведены в условии этой задачи.
3. Изгиб с кручением прямых круглых валов
3.1. Общие сведения
К
руглые
валы являются наиболее часто встречающимися
элементами механизмов и машин. Валы
служат для передачи крутящего момента
и сил между деталями, вращающимися
вместе с валом. Такими деталями могут
быть зубчатые колеса зубчатых передач,
шкивы ременных передач, ролики фрикционных
передачи звездочки цепных передач. При
работе таких передач возникают силы
различной природы, образующие в общем
случае произвольную пространственную
систему сил.
Н
Рис. 3.1
На рисунке обозначено:
и
- диаметры зубчатых колес 1 и 2;
и
-
точки зацепления 1- го и 2- го колес с
колесами предыдущей и последующей
ступеней передачи;
-
угол между направлением на точку
относительно точки
,
измеренный относительно продольной
оси вала в направлении, противоположной
направлению вращения часовой стрелки;
и
окружные силы, приложенные к зубчатым
колесам 1 и 2 в точках зацепления
и
и направленные по касательным к
окружностям радиусов
и
,
проходящим через эти точки ;
и
- радиальные силы в зацеплениях колес,
линии действия которых проходят через
точки
и
перпендикулярно оси вала и направленные
к оси вала;
и
- осевые силы в зацеплениях колес,
проходящие через точки
и
и направленные параллельно оси вала;
,
,
- длины участков вала.
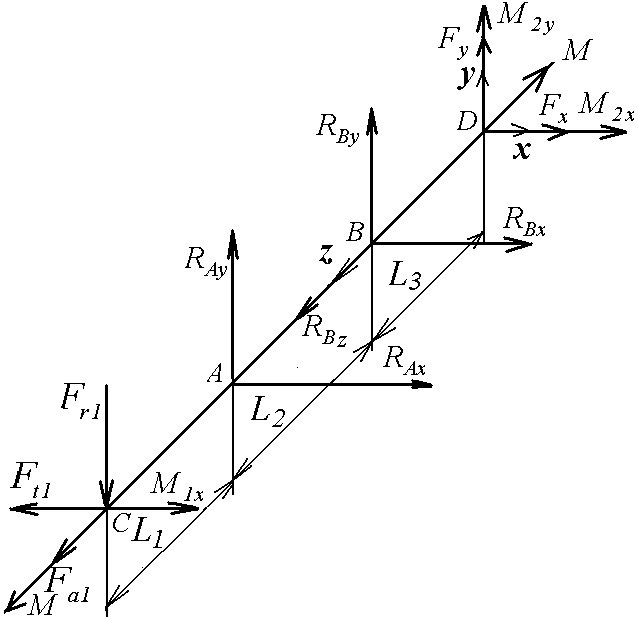
В
Рис.
3.2
В зависимости от вида колес осевые силы и в зацеплениях колес могут иметь другие направления или отсутствовать.
Если величина осевой силы отрицательна, то это значит, что соответствующая сила имеет направление, противоположное направлению, указанному на расчетной схеме вала (рис. 9 [3]).
Для
учета реальных направлений окружных
и осевых сил и получения универсальных
формул, верных для всех вариантов
исходных данных, удобно использовать
величины
и
.
Если
силы
и
направлены также, как и на схеме
нагружения вала, то принимают, что
=
1. В противном случае
=
-1.
Если
силы
и
направлены также, как и на схеме
нагружения вала, то принимают, что
=
1. В противном случае
=
-1.
Послу введения коэффициентов и вместо векторов , , следует использовать векторы , , .
Вращающий
момент, передаваемый зубчатыми колесами
определяется по формуле
.
В валах механизмов возникают в общем случае нормальные напряжения от нормальных сил и изгибающих моментов и касательные напряжения от крутящего момента и поперечных сил. В общем случае в точках вала наблюдается объемное напряженное состояние.
Построение расчетных схем валов в сопротивлении материалов не рассматривается, поскольку требует знания общетехнических дисциплин, в частности теории механизмов и машин и деталей машин.
В общем случае на вал, как твердое тело, действует пространственная система сосредоточенных сил, создающая моменты произвольных направлений.
При расчете валов используются ранее рассмотренные методы определения напряжения при растяжении- сжатии, изгибе балок и чистом кручении валов.
Существует три вида расчетов валов - расчет на прочность, расчет на жесткость и расчет на выносливость.
Перед проведением расчетов любого вида необходимо построить эпюры внутренних силовых факторов в поперечных сечениях вала.
Расчетная практика показывает, что в общем случае напряжениями от нормальных и поперечных сил в сравнении с напряжениями от крутящих и изгибающих моментов можно пренебречь.
3.2. Определения реакций опор вала
Поскольку
положение точки
на окружности диаметра
произвольно перед определением опорных
реакций систему сил, приложенных к
валу, следует привести к точкам
и
продольной оси вала, в которых эта ось
пересекается с плоскостями, проходящими
через точки
и
ортогонально этой оси. При приведении
сил используется теорема Вариньона и
известное утверждение статики «силу,
приложенную к абсолютно твердому телу,
можно не изменяя ее действия на тело,
переносить параллельно ей самой в любую
точку тела, добавляя при этом пару сил
с моментом, равным моменту переносимой
силы относительно точки, в которую
переносится эта сила».
Для
определения момента
силы
,
приложенной в точке
,
относительно точки
используется формула
,
где
вектор – радиус точки
,
начало которого находится в точке
.
Вектор направлен ортогонально плоскости, содержащей векторы и , в ту сторону, глядя откуда можно видеть вращение, которое может вызвать сила , происходящим против хода часовой стрелки.
При решении задач более удобной является формула
,
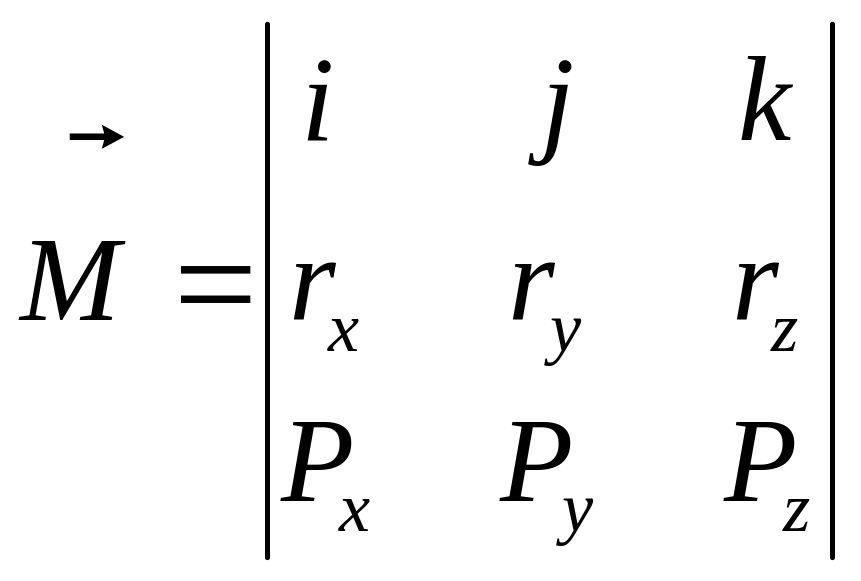где
- орты осей
системы координат;
- проекции вектора
на оси координат;
- проекции силы
на оси координат.
После раскрытия определителя в последней формуле получаем
,
, (3.1)
.
Вектор
– радиус точки
с началом в точке
имеет проекции
,
,
.
После
переноса сил
в
точку
продольной оси вала получаем силу
с проекциями
,
, (3.2)
,
и
момент
с проекцими, определяемыми по формулам
(3.1)
,
, (3.3)
.
Вектор – радиус точки с началом в точке имеет проекции
,
,
.
После
переноса сил
в
точку
продольной оси вала получаем силу
с проекциями
,
(3.4)
,
и
момент
с проекциями, определяемыми по формулам
(3.1)
,
, (3.5)
.
Для упрощения расчетов рассматривается раздельное воздействие на вал сил, расположенных в вертикальной и горизонтальной плоскостях.
Вал
опирается на подшипники
и
.
В расчетах опору
считают шарнирно – подвижной, а опору
- шарнирно – неподвижной. Поэтому от
действия осевых сил реакция возникает
только в опоре
.
3.2.1.
Определение реакций в вертикальной
плоскости
(
В
вертикальной плоскости действуют силы
,
,
,
,
а также пары сил, образующих моменты
и
.
Действие этих сил уравновешивается
реакциями
,
и
Уравнения равновесия сил и моментов сил, приложенных к валу в вертикальной плоскости, относительно точек А и В имеют вид
,
, (3.6)
. (3.7)
Первое уравнение для всех схем нагружения вала одинаково и имеет вид
.
Поэтому осевая реакция в опоре определяется по формуле
. (3.8)
Вид уравнений (3.6) и (3.7) системы зависит от взаимного рас- положения опор и колес.
Таблица 1
№ сх. |
Уравнения
равновесия моментов сил относительно
точек А
и
В
и выражения для определения реакций
в плоскости
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Таблица 2
№ сх. |
Уравнения
равновесия моментов сил относительно
точек А
и
В
и выражения для определения реакций
в плоскости
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
Уравнения равновесия моментов сил относительно точек А и В и выражения для определения реакций в плоскости приведены в табл. 1.
Для
проверки правильности определения
реакций
и
можно использовать уравнение
.
3.2.2.
Определение реакций в горизонтальной
плоскости
(
В
вертикальной плоскости действуют силы
,
,
а также пары сил, образующих моменты
и
.
Действие этих сил уравновешивается
реакциями
,
.
Уравнения равновесия сил и моментов сил, приложенных к валу в горизонтальной плоскости, относительно точек А и В имеют вид
, (3.9)
. (3.10)
Для
проверки правильности определения
реакций
и
можно использовать уравнение
.
Вид
уравнений (3.9) и (3.10) системы зависит от
взаимного расположения опор и колес.
Уравнения равновесия моментов сил
относительно точек А
и
В
и выражения для определения реакций в
плоскости
приведены в табл. 2.
3.3. Построение эпюр внутренних силовых факторов
в поперечных сечениях вала
Поскольку нормальные напряжения от нормальных сил и касательные напряжения от поперечных сил значительно меньше нормальных напряжений, вызванных изгибом, и касательных напряжений, вызванных кручением, для расчетов вала на прочность и жесткость строятся эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях и эпюра крутящих моментов.
Для
определения внутренних силовых факторов
в поперечных сечениях вала используется
метод сечений. Для этого в нужном месте
вал рассекается поперечным сечением,
одна из частей вала с приложенными к
ней внешними силами и реакциями
отбрасывается, ее действие на оставленную
часть вала заменяется искомыми
внутренними силовыми факторами –
изгибающими моментами
и крутящим моментом
.
Величины
и
определяются из уравнений равновесия
оставленной рассматриваемой части
вала или по соответствующим правилам
знаков.
Изгибающие моменты определяются по формулам
,
,
где
и
- изгибающие моменты в сечении вала.
Моменты и в данном сечении вала определяются относительно главных центральных осей инерции этого сечения вала.
Момент (или ) считается положительным, если он в точках первой четверти сечения вызывает сжимающее нормальное напряжение.
Суммарный изгибающий момент в сечении вала определяется по формуле
.
В сечении вала, в котором хотя бы один из моментов ( или ) имеет разрыв, суммарный изгибающий момент должен определяться слева и справа от этого сечения.
Крутящий момент в поперечном сечении вала, нагруженного сосредоточенными моментами, определяется по формуле
,
где
- момент, приложенный к рассматриваемой
части вала.
В
основу этого соотношения положено
правило знаков, согласно которому
крутящий момент в рассматриваемом
сечении считается положительным, когда
вращает рассматриваемую часть вала
против хода часовой стрелки, если
смотреть в направлении, противоположном
направлению внешней нормали к сечению.
При
наличии в некотором сечении одновременно
действующих крутящего
и изгибающего
моментов в сечениях вала определяется
эквивалентный (приведенный) момент
=
.
В сечении вала, в котором хотя бы один из моментов ( или ) имеет разрыв, эквивалентный изгибающий момент должен определяться слева и справа от этого сечения.
3.4. Расчет вала на прочность
При расчете вала на прочность опасным сечением вала считается сечение, в котором максимален эквивалентный момент. Это сечение определяется по эпюре эквивалентного изгибающего момента.
Условие прочности вала имеет вид
,
где
= 50 МПа - заниженное допускаемое нормальное
напряжение материала вала;
- момент сопротивления сечения вала
при изгибе.
Диаметр вала определяется по формуле
.
Если в опасном сечении вала действует только крутящий момент , то диаметр сечения можно определить из условия прочности на кручение
,
где
= 0,5
- допускаемое касательное напряжение
материала вала.
3.5. Расчет вала на жесткость
С
целью уменьшения упругого мертвого
хода, особенно проявляющегося в точных
приборных (не силовых) механизмах
крутильная жесткость валов ограничивается
допускаемым углом закручивания
.
Условие жесткости вала на кручение
имеет вид
,
где
- допустимая величина угла закручивания
вала на рабочей длине
.
Рабочая длина вала определяется суммированием длин участков вала, на которых крутящий момент вала отличен от нуля.
В зависимости от точности механизма величину принимают равной нескольким угловым минутам.
Диаметр вала на участке, нагруженном только крутящим моментом, определяется по формуле
,
где
=8*104
МПа– модуль сдвига материала вала.
Если
модуль сдвига определяется в МПа, то
крутящий момент
можно подставлять в последнюю формулу
в Н*мм.
Если
условия жесткости вала не выполнено,
то есть
,
то в качестве диаметра вала принимают
наибольший из диаметров
и
.
Полученный диаметр выражают в миллиметрах и округляют до целого числа из предпочтительного ряда размеров, в котором числа заканчиваются цифрами 0, 2, 4, 5, 6 и 8.