
- •Задания и методические указания
- •Контрольная работа №1
- •Задача №1.1
- •Анализ разветвленной электрической цепи
- •Постоянного тока
- •Пример выполнения задания
- •Задача №1.2 Анализ линейной электрической цепи однофазного синусоидального тока
- •Пример выполнения задания
- •Контрольная работа №2 Анализ трехфазных цепей Задача № 2.1
- •Задача № 2.2
- •Пример решения задач
- •Библиографический список
- •Содержание
- •Задания и методические указания
- •151900.62 «Конструкторско-технологическое обеспечение
- •394026 Воронеж, Московский просп., 14
Пример решения задач
1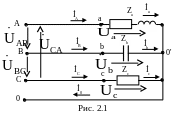 .
Определить линейные и фазные токи и
напряжения в трехфазной нагрузке,
соединенной по схеме звезда с нулевым
проводом, сопротивление которого равно
нулю (рис. 2.1).
.
Определить линейные и фазные токи и
напряжения в трехфазной нагрузке,
соединенной по схеме звезда с нулевым
проводом, сопротивление которого равно
нулю (рис. 2.1).
Питание осуществляется от источника электрической энергии, фазы которого соединены по схеме «звезда», напряжение фазы Uф = 127 В.
Параметры элементов цепи: R =XL=XС=100 Ом.
Рассчитать фазные и линейные токи и напряжения полнофазного режима цепи. Определить активную и реактивную мощности нагрузки. Построить векторную диаграмму токов и напряжений.
Так как сопротивление нулевого провода равно нулю, то напряжение смещения нейтрали в схеме отсутствует и фазные напряжения приемника равны соответствующим фазным напряжениям генератора:
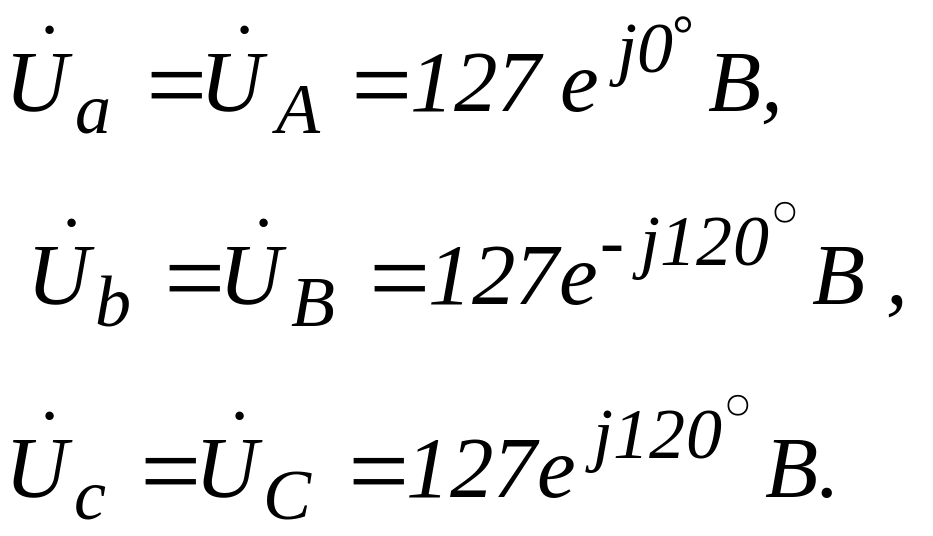 (2.1)
(2.1)
Сопротивления фаз нагрузки:
Zа= R+ jXL, (2.2)
Zb = -jXc, (2.3)
Zc =R, (2.4)
Zа=100+j100=141ej45° Ом,
Zb = -j100= 100e-j90° Ом,
Zc =100 Ом.
Фазные токи приемников определим по закону Ома:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
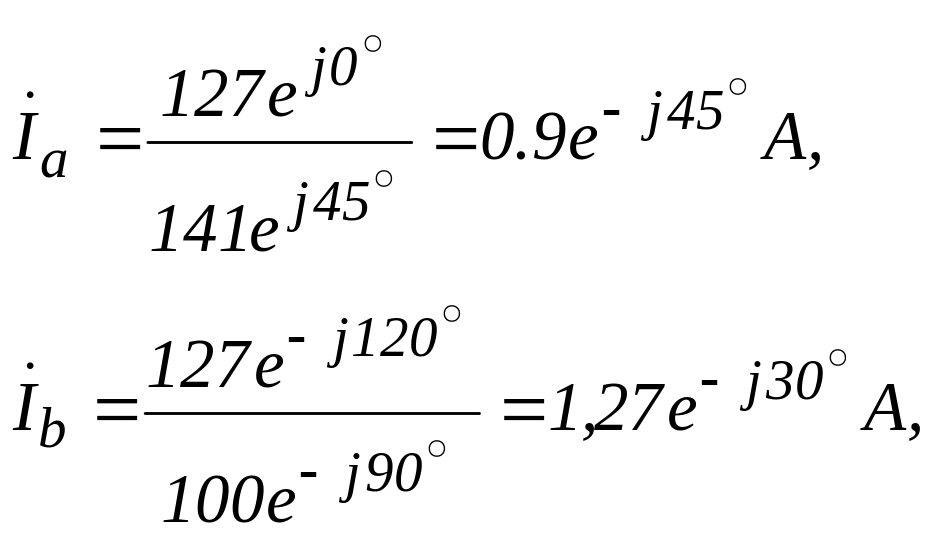
![]()
Ток в нулевом проводе определяется с помощью первого закона Кирхгофа:
![]() (2.8)
(2.8)
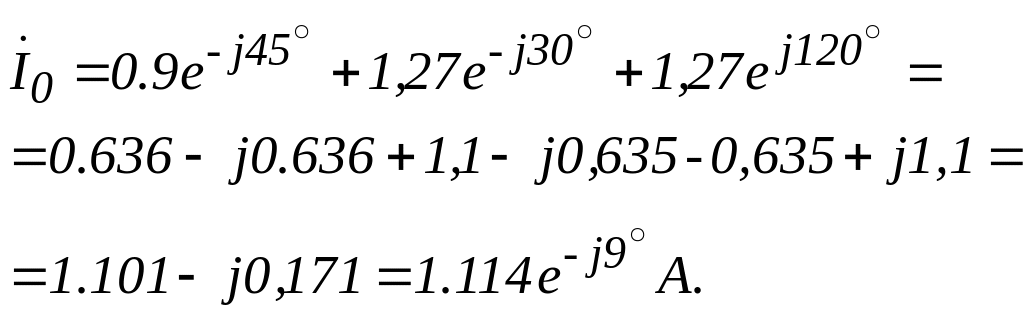
Активная, реактивная и полная мощности определяются следующим образом:
активная мощность приемников:
![]() (2.9)
(2.9)
![]()
реактивная мощность приемников:
![]() (2.10)
(2.10)
![]()
полная мощность:
![]() (2.11)
(2.11)
![]()
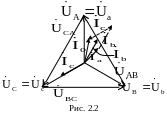
На комплексной плоскости построим векторную диаграмму токов и напряжений (рис. 2.2).
2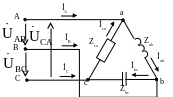 .
Определить линейные и фазные токи и
напряжения в трехфазной нагрузке,
соединенной по схеме треугольник (рис.
2.2). Построить векторную диаграмму
рассчитанных токов и напряжений.
.
Определить линейные и фазные токи и
напряжения в трехфазной нагрузке,
соединенной по схеме треугольник (рис.
2.2). Построить векторную диаграмму
рассчитанных токов и напряжений.
Рис. 2.3
Питание осуществляется от источника с линейным напряжением UЛ = 220 В, сопротивления фаз нагрузки:
Zаb= jXL, (2.12)
Zbc = -jXc, (2.13)
Zca = R, (2.14)
Zаb = j100 Ом,
Zbc = -j100 Ом,
Zca = 100 Ом.
Фазные напряжения приемников, при соединении фаз нагрузки треугольником, равны линейным напряжениям:
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]()
![]()
![]()
Фазные токи определяем с помощью закона Ома:
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
![]()
![]()
![]()
Линейные токи рассчитаем, воспользовавшись первым законом Кирхгофа:
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
![]() (2.23)
(2.23)
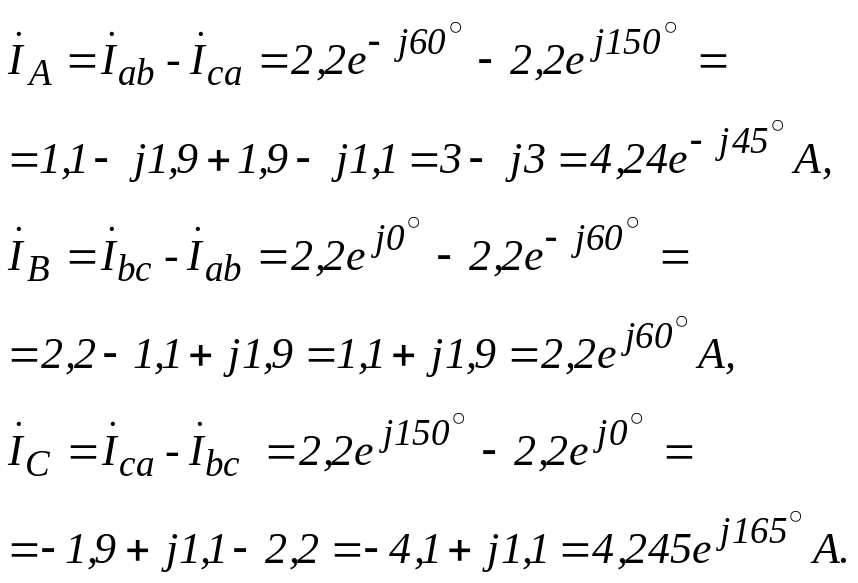
П
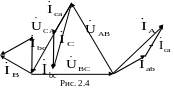 остроим
векторную диаграмму токов и напряжений
(рис. 2.4).
остроим
векторную диаграмму токов и напряжений
(рис. 2.4).
