
Сборник трудов победителей конкурса на лучшую научную работу студентов и аспирантов ВГТУ
.pdf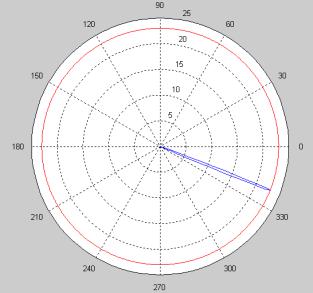
необходимо видоизменить. Интегрирование будет производиться не поверхности сферы, а по дуге окружности – двойной интеграл заменен на криволинейный. Угол υ=0 (как это видно из рисунка 1), следовательно, cos(υ)=1. Так для нахождения удельной мощности излучения изотропного излучателя целесообразно воспользоваться выражением (5):
PI _ I _ U 2 R 0 |
, |
(5) |
Для нахождения удельной мощности направленной антенны целесообразно воспользоваться выражением (6):
|
180 |
|
PI _ U |
|
Rd , (6) |
|
||
|
180 |
|
где Π – модуль вектора Пойнтинга. Таким образом, для нахождения ПКНД (D0_P) в направлении максимума излучения необходимо найти отношение удельной мощности излучения изотропного излучателя PI_I_U к удельной мощности излучения PИЗЛ_У направленной антенны (7):
|
180 |
|
|
|
|
D0 _ P 2 / |
|
F |
2 |
( )d , |
(7) |
|
|||||
|
|
||||
|
180 |
|
|
|
|
где F2(Θ) – нормированная плоская ДН направленной антенны.
Вкачестве примера целесообразно
привести расчетное значение ПКНД для дифракционной антенны со следующими характеристиками: число канавок – 43, период гребенки d=0.7λ, диэлектрическая проницаемость ε=2.56, ширина канавок a=0.3d, глубина канавок h=0.05d:0.38d, прицельное расстояние r=0.82d,
толщина диэлектрика τ=0.2d, ПКНД D0_P=152.8. На рисунке 2 представлена плоская ДН дифракционной антенны (синий цвет) и плоская ДН изотропной антенны (красный цвет).
Рис. 2. Плоская ДН направленной антенны (синий) и плоская ДН изотропного излучателя (красный)
Следует отметить следующее – использование понятия ПКНД является в некотором смысле вынужденной мерой, в случае неопределенности ДН в ортогональной плоскости. Понятие ПКНД было необходимо для модели [2], т.к. предложенная модель позволяет производить вычисление ДН в одной плоскости.
Таким образом, была предложена методика расчета ПКНД. ПКНД является хорошим индикатором направленных свойств антенны при синтезе в условиях неопределенности ДН в ортогональной плоскости.
Литература
1.Сазонов Д.М. Антенны и устройства СВЧ. – М.: Высшая школа, 1988. – 432 с.
2.Останков, А.В. Анализ и оптимизация дифракционной антенны поверхностной волны / А.В. Останков // Антенны. – 2010. – № 9 (160). – С. 44-53.
3.B. П. Шестопалов, Л. Н. Литвиненко, C. А. Масалов, В. Г. Сологуб. Дифракция волн на решетках. – Х.: Из-во ХГУ, 1973. – 288 с.
4.А. А. Пистолькорс. Антенны. – М.: Государственное издательство литературы по вопросам связи и радио, 1947. – 480 с.
60
УДК 94
ПОДГОТОВКА РАБОЧИХ НА ТЕРРИТОРИИ ЦЕНТРАЛЬНОГО ЧЕРНОЗЕМЬЯ В 30-Е ГГ. XX В.: ИСТОРИЧЕСКИЙ ОПЫТ
Аспирант кафедры истории и политологии Евстратов Антон Геннадьевич Руководитель: д-р ист. наук, проф. Душкова Н.А.
В статье раскрываются особенности построения системы технического образования рабочих в период социалистической индустриализации на территории Центрально-Черноземного региона. Выясняются основные предпосылки, ход и итоги данного процесса
Модернизация экономики, техническое и организационное ее преобразование, как в первой половине XX в., так и в настоящее время невозможно без достаточного количества подготовленных кадров. Квалифицированные исполнители необходимы во всех отраслях и на всех уровнях производства, особенно развивающегося ускоренными, форсированными темпами. Именно с проблемой нехватки необходимого числа рабочих, техников, инженеров и администраторов столкнулось правительство СССР в начале индустриализации.
Учитывая столь же сложную ситуацию с профессионально-технической подготовкой рабочего класса в условиях модернизации современной России, настоящее исследование может быть актуально и для наших дней.
Ко времени первых индустриальных преобразований, ситуация с кадрами на территории всего Советского Союза была тревожной. Пополнение стремительно увеличивавшегося рабочего класса приходило, прежде всего, из деревни. Часто новых рабочих следовало обучать не только профессиональному мастерству, но и элементарной грамоте [1, 21].
Что касается Центрального Черноземья, то на территории этого региона ситуация была еще более сложная, чем в целом по стране. Дело в том, что данная местность являлась аграрной, и
92,5 процента ее населения проживало в сельской местности [7, 17]. На всей территории Центрального Черноземья, объединенного в 1928 году в Центрально-Черноземный Округ (ЦЧО), к началу первой пятилетки насчитывалось лишь 6 крупных предприятий с 9 тысячами рабочих. В 12 типографиях региона трудилось дополнительно 560 человек. В то же время партия и правительство поставили задачу превращения региона из аграрного в аграрно-индустриальный, что подразумевало значительный количественный рост промышленности, а также введение новых технологий производства.
Следует отметить, что количество рабочих в регионе только за первую пятилетку увеличилось в 2 раза, причем на предприятиях группы А было зафиксировано четырехкратное увеличение количества персонала. По большей части из деревни на фабрики и заводы шли неграмотные и малограмотные крестьяне. Пополнявшие ряды рабочих юноши и девушки, имевшие некоторый уровень подготовки (окончившие начальные и
неполные средние школы с семилетним сроком обучения) [7,22], составляли незначительное количество, если учесть, что никакого образования не имело 34,9% жителей сел ЦЧО [Там же].
Чтобы закрепить работников на предприятиях, поднять производительность труда, на территории Центрального Черноземья с начала первой пятилетки начала создаваться широкая сеть учреждений технического обучения рабочих. Они были представлены школами фабрично-заводского ученичества (ФЗУ), кружками технического минимума, учреждениями индивидуального обучения, а также школами по ликвидации малограмотности [7, 26].
Программа модернизации системы технического обучения в законченной форме была изложена в постановлении ЦК ВКП(б) от 19 ноября 1931 года «О постановке технической пропаганды и технического обучения рабочих». В том же году партия выдвинула лозунг «Кадры, овладевшие техникой, решают все». Только на подготовку квалифицированных рабочих, мастеров и инженеров для цензовой промышленности (то есть предприятий с числом рабочих не менее 16 при наличии механического двигателя и не менее 30 — без двигателя) Центрально-черноземной области в 1929 году ассигновалось 2,5 миллиона рублей, а двумя годами позже – 6,5 миллиона. Помимо государственного финансирования, оплата обучения была возложена и на самих трудящихся, которые покупали займы технической учебы [2, 135].
Огромная работа проводилась по ликвидации полной и частичной безграмотности. Уже в 1929 году сетью кружков ликбеза было охвачено 260 тысяч человек, а на следующий год количество обучавшихся в них превысил 1,3 миллиона.
Что касается школ ФЗУ, то они были, как правило, трех типов. Первый готовил контролеров, помощников мастеров и т. д. Второй – слесарей, токарей, фрезеровщиков. Третий – рабочих массовых профессий. Известно, что только в 19301931 гг. в такие школы по Центральному Черноземью поступило 28,5 тысяч человек [7, 27].
Часто образовательные учреждения, курсы, школы и даже ВУЗы создавались прямо на предприятиях. Учебу в подобных учреждениях старались как можно теснее связать с производством. Рабочим же, проходящим соответствующую подготовку, делались многочисленные послабления. Так, рабочие, учившиеся на заводе имени Дзержинского,
61
сохраняли свой средний заработок, день отдыха, |
Немалую пользу можно извлечь из опыта |
|||||||||||
годовой отпуск, 7-часовой рабочий день на |
подготовки кадров для индустриализации 30-х годов |
|||||||||||
производстве. Вместе с тем, от 6 до 8 часов в |
прошлого века и для наших дней. На данный |
|||||||||||
пятидневку «студенты» должны были отдавать |
момент в России, фактически, разрушена система |
|||||||||||
учебе [6, 324]. |
|
|
|
|
профессиональной подготовки рабочих, которая |
|||||||
Помимо |
указанных |
учреждений технической |
необходима для модернизации и построения нового |
|||||||||
подготовки рабочих, инженеров и администраторов |
технологического уклада. Во многом ситуация |
|||||||||||
предприятий, существовали также рабфаки, |
схожа с той, что наблюдалась в конце 20-х гг. |
|||||||||||
призванные подготовить пролетарский контингент к |
прошлого столетия. Только создание новой, |
|||||||||||
поступлению в ВУЗы и получению его |
прогрессивной системы подготовки рабочих кадров |
|||||||||||
представителями высшего образования. На рабфаки |
для инновационной |
промышленности |
способно |
|||||||||
принимались как лица, уже прошедшие низшие |
вывести модернизацию страны за рамки дискуссий в |
|||||||||||
ступени обучения (начальные школы, школы ФЗУ, и |
плоскость реальных мероприятий. Серьезной |
|||||||||||
т. д.), так и малограмотные абитуриенты. [5, 1]. |
проблемой современной России, помимо отсутствия |
|||||||||||
Часто там оказывались люди, с трудом умевшие |
необходимой инфраструктуры, является также |
|||||||||||
читать. |
|
|
|
|
сформировавшееся в последние годы общественное |
|||||||
При учреждении новых учебных заведений |
сознание, из-за которого рабочие профессии |
|||||||||||
часто стояла проблема нехватки преподавательских |
потеряли престижность. Именно для реализации |
|||||||||||
кадров. Профессорско-преподавательский состав |
данной задачи государство должно поддерживать |
|||||||||||
часто формировался на ускоренной основе. Что |
высококвалифицированных рабочих, ориентировать |
|||||||||||
касается учебных комбинатов, рабфаков или |
их на получение образования для формирования |
|||||||||||
рабочих университетов, то в этих, по сути, |
среднего |
слоя |
|
– |
|
главной |
опоры |
|||||
учреждениях высшей школы часто занятия вели |
постиндустриального |
|
общества, |
|
общества |
|||||||
бывшие учителя гимназий, училищ и школ среднего |
будущего. |
|
|
|
|
|
|
|
||||
звена [6, 314]. Естественно, это должно было |
|
|
|
Литература |
|
|
||||||
сказываться на качестве знаний студентов. |
|
|
|
|
|
|
|
|
|
|||
Имел место ряд серьезных проблем. Не все |
1. |
Демидов |
Р. |
Г. |
Социалистическая |
|||||||
поступившие в упомянутые выше образовательные |
индустриализация ЦЧО в годы первой пятилетки. |
|||||||||||
учреждения успешно их заканчивали. Имел место |
Автореферат диссертации на соискание ученой |
|||||||||||
значительный отсев. В частности, в 1930 году из 13 |
степени кандидата исторических наук – Воронеж, |
|||||||||||
тысяч поступивших успешно окончили школы ФЗУ |
1975. |
|
|
|
|
|
|
|
||||
только 5095 человек. [7, 27]. Причинами столь |
2. |
Демидов Р. Г., Кривцун И. В. |
||||||||||
значительного отсева являлись, как уже упомянутый |
Социалистическая |
|
индустриализация |
|
и рост |
|||||||
низкий уровень знаний рабочих, не дававший им |
культурно-технического |
уровня |
трудящихся |
|||||||||
возможность развиваться и продолжать обучение на |
Центрального Черноземья (1928-1941 гг) – Воронеж, |
|||||||||||
более высоких ступенях, так и порой слишком |
1978. – 363 с. |
|
|
|
|
|
|
|||||
напряженный режим, требовавший от студентов |
3. |
ГАВО, ф. Р-1062, оп. 1, д. 1. |
|
|
||||||||
совмещать |
учебу |
с |
работой. |
Часто |
4. |
ГАВО, ф. Р-1062, оп. 2, д. 1. |
|
|
||||
преподавательский состав и мастера различных |
5. |
ГАВО, ф. Р-1636, оп. 1, д. 155. |
|
|||||||||
кружков и профессионально-технических училищ |
6. |
История |
индустриализации |
Центрально- |
||||||||
не относился к своим обязанностям достаточно |
Черноземного района 1926-1932 гг. (сборник |
|||||||||||
ответственно. Это объяснялось отсутствием |
документов), т. 1 – Воронеж: Центрально- |
|||||||||||
материальной заинтересованности. Так в Воронеже |
Черноземное книжное издательство, 1970. – 495 с. |
|||||||||||
мастера школ ФЗУ получали к своему жалованью на |
7. Климов И. М. Из истории формирования |
|||||||||||
заводах дополнительно 8%, и поэтому доверяли |
рабочего класса Центрального Черноземья / И. М. |
|||||||||||
ученикам лишь устаревшие инструменты или вовсе |
Климов. – Воронеж: Издательство Воронежского |
|||||||||||
заставляли тех выполнять не имеющую отношения к |
госуниверситета, 1977. – 70 с. |
|
|
|
||||||||
обучению работу (а в наиболее курьезных случаях – |
|
|
|
|
|
|
|
|
||||
посылали студентов за папиросами) [6, 135]. |
|
|
|
|
|
|
|
|
||||
Немалые |
проблемы |
испытывали |
новые |
|
|
|
|
|
|
|
|
|
образовательные учреждения и с помещениями, а |
|
|
|
|
|
|
|
|
||||
также со специальной литературой. Последняя |
|
|
|
|
|
|
|
|
||||
трудность была связана с тем, что необходимо было |
|
|
|
|
|
|
|
|
||||
готовить учебники, соответствовавшие уровню |
|
|
|
|
|
|
|
|
||||
подготовки студентов новых учреждений. Тем не |
|
|
|
|
|
|
|
|
||||
менее согласованные действия правительства, |
|
|
|
|
|
|
|
|
||||
администраций учебных заведений и предприятий |
|
|
|
|
|
|
|
|
||||
со временем решили поставленную задачу. |
|
|
|
|
|
|
|
|
||||
Выросшая количественно и преобразован-ная |
|
|
|
|
|
|
|
|
||||
качественно |
промышленность региона |
получила |
|
|
|
|
|
|
|
|
||
достаточное число рабочих, инженерных и |
|
|
|
|
|
|
|
|
||||
административных кадров, которые обеспечили |
|
|
|
|
|
|
|
|
||||
работу его предприятий на высоком уровне. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
62 |
|
|
|
|
|
|
|
УДК 519.673
ПОСТРОЕНИЕ ПРОГНОСТИЧЕСКИХ МОДЕЛЕЙ ВОЗНИКНОВЕНИЯ ПАВОДКА С ИСПОЛЬЗОВАНИЕМ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Студент группы ИС-091 Долженкова Виолетта Владимировна Студент группы ЧС-091 Киреев Дмитрий Олегович Руководитель: канд. техн. наук, доц. Звягинцева А.В.
Рассматриваются возможные технические решения организации системы автоматизированного мониторинга и оперативного прогнозирования максимального стока. На основе пространственного анализа с применением ГИС-технологий дан прогноз затопления территории в нижнем течении реки Битюг
В настоящее время информация о гидрологическом режиме рек и водоемов, необходимая для анализа риска развития половодья и прогноза основных его характеристик, имеется в основном, только для небольшой части речной сети, где сохранилась явно не достаточная сеть гидрометеорологических станций и постов, измерения на которых производятся с применением в основном устаревших методов и измерительных приборов. Особое значение в вопросе повышения качества, как входной гидрометеорологической информации, так и получаемых прогнозов, играет не только усовершенствование способов измерения (определения) [1,2], но совершенствование методологии мониторинга гидрологических характеристик. В данной работе показана взаимосвязь пространственного анализа и географических систем на конкретном объекте одной территории. Целью данной работы является разработка прогноза затопления территории в нижнем течении реки Битюг на основе пространственного анализа с применением ГИСтехнологий. Актуальность работы обусловлена особенностью затопления территории нижнего течения реки Битюг, что влияет на разработку прогноза ЧС гидрологического характера [3].
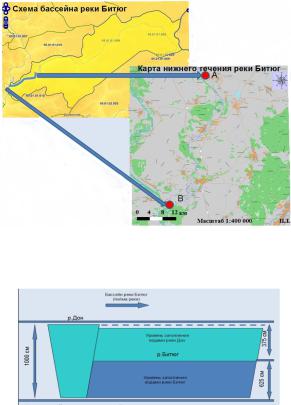
В работе применялись следующие программные средства: пакет статистического анализа Statistika, сервис по построению зон затопления «floodmap», географическая информационная система ArcGIS. В нижнем течении реки Битюг находятся следующие населенные пункты: х. Ступино, с. Лосево, х. Безымянный, х. Чугуновка, х. Антиповка, х. Серов, с. Шестаково, пос. Малый Кисляй, с. Мечетка – при соответствующих подъемах уровней воды в реке Битюг возможно попадание некоторых населенных пунктов в зону затопления (рис.1). На водный режим нижнего Битюга оказывает влияние подпор воды Дона: в устье Битюга уровень воды резко повышается при высоком половодье на Дону, донская вода разливается по пойме Битюга вверх на 30-40 км (можно видеть обратное течение и медленное движение льдин вверх, на север), (рис. 2). Таким образом, на прогнозирование гидрологических явлений в нижнем течении реки Битюг оказывают влияния не только показатели по бассейну реки, но и показатели подъема уровня воды в реке Дон. Для решения задач прогнозирования развития паводковой обстановки
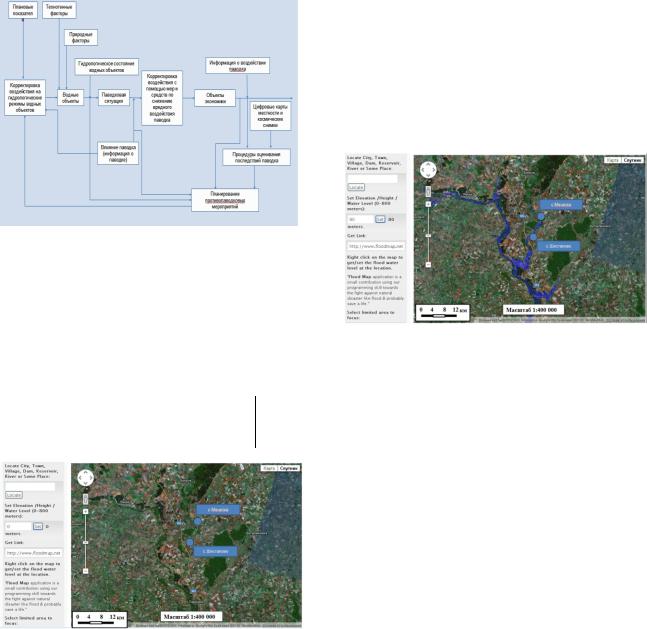
наиболее удобным является применения географических информационных систем, для этого предлагается построить систему в основу которой будет положена представленная схема информационного взаимодействия (рис. 3).
Рис.1. Схема бассейна реки Битюг и карта нижнего течения реки Битюг. Обозначение: точка А – река Битюг у села Мечетка, точка В – место впадения реки Битюг у села Шестаково
Рис. 2. Особенности затопления территории в нижнем течении реки Битюг (схематичное отображение створа впадения р. Битюг в р. Дон)
База геоданных о зонах затопления должна содержать различные общеографические слои, специальные слои, содержащие сведения гидрологического характера и растровые данные в виде космоснимков [4,5]. При осуществлении разработки краткосрочных и оперативных прогнозов развития обстановки необходимо использовать текущие данные об уровнях воды на гидропостах [5]. Модель затопления территории нижнего течения реки битюг представлена на рис. 4, 5 в зоне затопления находятся два населенных пункта – села Мечетка и Шестаково. Показана карта зоны затопления нижнего течения реки Битюг при отметке 80 м по Балтийской системе высот по данным космических снимков. Количество жилых построек населенных пунктов
63
Мечетка и Шестаково попадающих в зону затопления при различной площади разлива реки Битюг, определяемой уровнем подъема воды (раличной обеспеченности половодья) представлено в таблице.
Рис. 3. Пространственная информация о зоне затопления и объектах попавших в зону затопления
Характеристика зоны затопления в зависимости от уровня подъема воды в реке Битюг
|
|
|
Количество домов, |
||||
|
|
Площадь |
затапливаемых |
|
|||
|
|
наивысшим |
|
||||
Населенный |
|
затопления |
|
||||
Река |
уровнем |
воды с |
|||||
пункт |
р=1%, |
||||||
|
вероятностью |
|
|||||
|
|
км.кв. |
|
||||
|
|
превышения р% |
|||||
|
|
|
|||||
|
|
|
1 |
5 |
1025 |
50 |
|
Мечетка |
Битюг |
0,05 |
34 |
27 |
6 0 |
0 |
|
Шестаково |
Битюг |
0,87 |
280 |
125 |
200 |
0 |
|
Рис. 4. Карта нижнего течения реки Битюг при отсутствии затопления
Таким образом, в работе определен порядок проведения работ и применения данных при прогнозировании ЧС гидрологического характера в нижнем течении реки Битюг, построены модели зон затопления сел Мечетка и Шестаково при 1 и 50% обеспеченности половодья. Определено что, при 1% обеспеченности половодья в зону
затопления попадают: в селе Мечетка 98 человек (в том числе 12 детей), проживающие в 34 жилых домах, в селе Шестаково 800 человек (в том числе 130 детей), проживающие в 280 жилых домах. Подводя итог, следует отметить, что пространственный анализ – это инструмент для анализа данных, объяснения их взаимоотношений и особенностей, выявления пространственновременных закономерностей. Пространственный анализ не дает окончательных ответов, он лишь констатирует некие факты и объясняет некоторые явления, которые требуют дальнейших исследований и либо приводит к подтверждению полученных результатов, либо к опровержению.
Рис.5. Подъем уровня воды до отметки 80 м (50 % обеспеченность половодья)
Литература
1.Ian N. Gregory and Paul S. Ell. HISTORICAL GIS: Technologies, Methodologies and Scholarship / Ian N. Gregory, Paul S. Ell. UK: Cambridge University Press, 2007. 241 p.
2.Кунгурцев С.А. Автоматизированная система оперативного оповещения о разливах рек /С.А. Кунгурцев, С.А. Жуков, В.И. Соловьев, М.В. Кумани, А.В. Апухтин // Экологические системы и приборы. 2012. № 4 С. 48–51.
3.Соколова Ю.П. Прогнозирование опасных метеорологических явлений при определении характера и масштабов стихийных бедствий:
монография |
/Ю.П. Соколова, А.В. Звягинцева, |
|||||
И.П. |
Расторгуев. |
Воронеж: |
ГОУ |
ВПО |
||
―Воронежский |
государственный |
технический |
||||
университет‖, 2009 г. |
215 с. |
|
|
|
||
4.Портал |
правительства |
Воронежской |
||||
области. |
Электронные |
данные |
Режим |
|||
доступа:http://www.govvrn.ru/wps/portal/AVO. |
||||||
5. Водный регистр и |
кадастр. |
Электроные |
||||
данные. Режим доступа: http://www.waterinfo.ru/
64

УДК 622.24
ПОСТРОЕНИЕ ПРОГНОСТИЧЕСКИХ МОДЕЛЕЙ РАСПРОСТРАНЕНИЯ ХИМИЧЕСКИ ОПАСНЫХ ВЕЩЕСТВ В ВОДНЫХ АКВАТОРИЯХ
С ИСПОЛЬЗОВАНИЕМ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Инженер кафедры ТОГОЧС Барковская Дарья Владимировна Руководитель: канд. техн. наук, доц. Звягинцева А.В.
Показана возможность отображения пространственных объектов в географических информационных системах. Рассмотрено распространение нефти по поверхности полигонального водного объекта. Проведен расчет распространения нефти для двух условий течения: по поверхности водоема (Воронежского водохранилища) и водотока (реки Дон)
Введение
При моделировании аварий, вследствие которых происходит разлив нефти или нефтепродуктов по водной поверхности, как правило, рассматривают две разновидности аварийного процесса.
Один из них - залповый сброс нефти, при котором практически мгновенно на поверхности водоема оказывается заданное количество нефти или нефтепродукта.
Второй разновидностью аварийного процесса разлива нефтепродуктов на водной поверхности является, постепенный вылив нефти через пробоину определенных размеров в корпусе танкера.
Существо задачи состоит в определении размеров нефтяного пятна на водной поверхности в виде зависимости радиуса и скорости дрейфа от времени.
Объектом исследования в работе являются полигональные водные объекты – водоемы и водотоки с установившимся режимом течения. Цель работы - построить прогнозные модели распространения нефти по поверхности полигональных водных объектов, конкретно водотоков с установившимся режимом течения и водоемов. Применяемые программные средства: пакет статистического анализа Statistika, программный комплекс WATER, географическая информационная система ArcGIS (с дополнительным модулем «Разлив нефтепродуктов
(вода))».
Прогнозирование распространения нефти на полигональных водных объектах на основе географических информационных систем
Теоретически при оценке распространения пятна аварийного разлива нефти и нефтепродуктов на поверхности воды включают в рассмотрение четыре стадии: инерционная; гравитационновязкостная; поверхностного натяжения; диффузионная.
Первые три стадии относятся к процессу растекания нефтепродуктов по поверхности водной среды и описываются приближенными аналитическими выражениями. Четвертая (диффузионная) стадия распространения нефтепродуктов непосредственно связана с динамическими процессами в районе разлива и поддается исследованию только с помощью методов математического моделирования.
Рассмотрим залповый (почти мгновенный) сброс нефтепродуктов в воду. В основе оценок по растеканию нефти и нефтепродуктов по водной поверхности (упрощенный вариант для случая несжимаемой и невязкой жидкости) лежит уравнение:
dr |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
( |
g (1 |
ж |
)) |
2 |
h |
2 |
|
|
|
|||||
|
|
, |
|
(1) |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
в |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где =1.34 –коэффициент, |
|
ж |
– |
|
плотность |
|||||||||
растекающейся |
жидкости |
|
|
(нефти |
или |
|||||||||
нефтепродукта), |
в – плотность |
|
|
воды |
водоема |
|||||||||
(моря), h – высота цилиндра разлива нефти. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значение коэффициента |
|
1 |
|
ж |
|
, |
учитывает |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
в |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
степень погружения нефтепродукта в воду. Определение времени подхода зоны
загрязнения с максимальной концентрацией аварийно химически опасного вещества к заданному створу. Прогноз времени подхода зоны загрязнения с максимальной концентрацией опасного вещества к заданному створу водотока определяется по формуле:
t |
|
t |
|
|
t |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
max |
|
Д |
|
2 |
|
|
|
|
|
|
|
(2) |
||
|
|
|
|
|
|
|
|
где |
t |
Д |
|
- время добегания речной воды от |
||||||||
|
|
|||||||||||
|
|
|
||||||||||
места аварии до заданного створа, час; |
|
|||||||||||
t |
0 |
- |
|
продолжительность сброса опасного |
||||||||
|
|
|||||||||||
|
|
|
||||||||||
вещества в реку, час. |
|
|
|
|
|
|||||||
Расчет |
t |
Д |
выполняется по формуле: |
|
||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
t |
|
|
L |
|
|
|
|
|
|
|
|
|
Д |
3,6V |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
, |
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
L |
- |
длина расчетного участка реки, |
км; |
||||||||
|
|
|||||||||||
V - средняя скорость течения реки на участке, м/с. Для моделирования разливов нефти с
применением ГИС предлагается использовать ГИСсистему с представленной на слайде архитектурой построения. Файловая база геоданных имеет следующий состав (рис. 1).
65
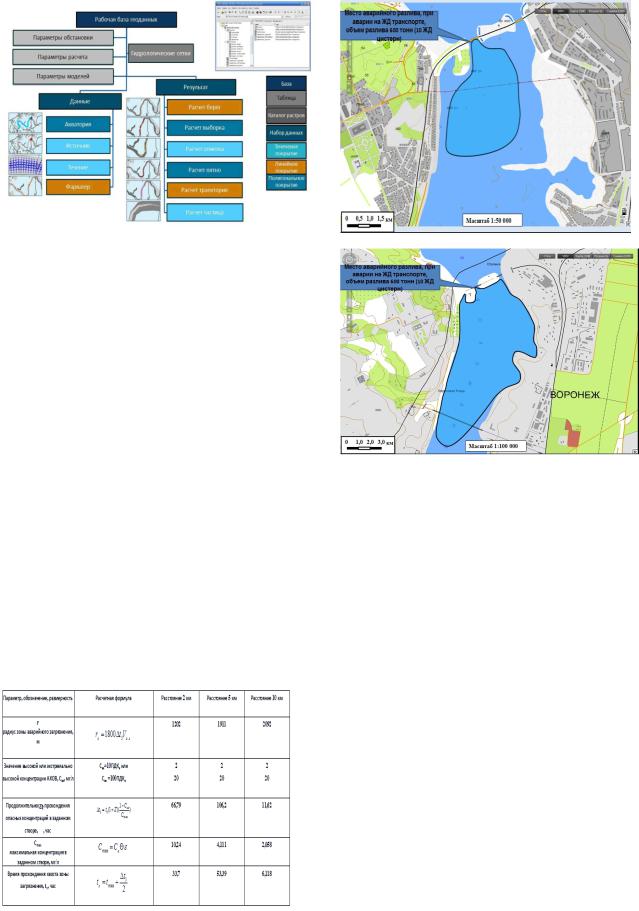
Рис. 1. Состав файловой базы географических данных
В работе применен метод графов, результаты моделирования с указанием источника разлива нефти представлены в работе [1].
Для установления влияния типа полигонального водотока на распространение нефти проведен расчет распространения нефти для двух условий течения: загрязнение реки Дон (поверхность водотока) и загрязнение Воронежского водохранилища (поверхность водоема). Далее представлены результаты моделирования для поверхности водоема:
- загрязнение акватории Воронежского водохранилища - наименование опасного вещества поступившего в водный объект - нефть, продолжительность сброса - 0,5 часа, Объем сбрасываемого вещества – 60 м3, концентрация вещества в загрязняющем сбросе – 850 мг/л, средняя скорость течения воды вдоль расчетной траектории - 0,01 м/с, средняя скорость течения в заданном створе – 0,01 м/с, средневзвешенное значение глубины водоема - 2 м, средневзвешенный коэффициент дисперсии – 3,6 м2/с, температура воды – 20 ºС.
Расчетные параметры, используемые при моделировании распространения нефти по поверхности водоема
Рис. 2. Модель распространения нефти по площади акватории Воронежского водохранилища на основе расчетных створов при аварии на железнодорожном транспорте
Сведения, полученные в результате расчетов, представлены в таблице для водоема. На рис.2 показана модель распространения нефти по акватории Воронежского водохранилища. Основное отличие условия распространения загрязнителя по акватории водоема от распространения по акватории водотока, является отсутствие установившего течения.
Выводы
Таким образом, в работе показано, что применение пространственного анализа при прогнозировании разливов нефти и нефтепродуктов на водных акваториях позволяет учесть основные физико-химические свойства нефти, влияющие на распространение нефти в воде, основные виды транспорта, применяемые для транспортировки нефти, информацию о крупных разливах нефти и нефтепродуктов на водных объектах.
Литература 1. Барковкая Д.В., Звягинцева А.В.
Пространственный анализ в информационных системах неотъемлемая часть мониторинга и прогнозирования распространения нефти на полигональных водных объектах //Сборник трудов ХХ международной научнотехнической конференции, 2013. Т.1. С. 248-252.
66
УДК 519.65+519.644.2
ПРЕДЕЛЬНОЕ ПОВЕДЕНИЕ КОРНЕЙ СКОЛЬЗЯЩИХ ЛАКУНАРНЫХ МНОГОЧЛЕНОВ ДЛЯ ДВУСТОРОННЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ ЧИСЕЛ ФИБОНАЧЧИ
Студент группы ВМ(м)-121 Шелудяков Алексей Николаевич Руководитель: д-р техн. наук, доц. Агранович Ю.Я.
В работе показано, что корни лакунарных многочленов скользящих вдоль последовательности чисел Фибоначчи вправо стремятся к вершинам правильных многоугольников, вписанных в окружность с радиусом равным «золотому сечению», а при сдвиге влево - к многоугольникам, инверсным относительно единичной окружности
Процессы скользящего суммирования чрезвычайно часто используются для обработки динамических рядов и давно снискали себе репутацию надежного метода извлечения информации из числовых данных. Некоторые недавние результаты, полученные в области весового скользящего сглаживания методом многоугольных чисел [1,2,3] показывают важность полиномиальных интерполяций при выборе ширины и расположения окна сглаживания[4,5,6,7,8,9]. В связи с этим возникает ряд новых неожиданных задач. Одна из таких задач состоит в исследовании предельного поведения корней многочленов с коэффициентами, скользящими вдоль некоторой
числовой |
последовательности, |
определенной |
||
линейным |
рекуррентным |
соотношением |
с |
|
постоянными коэффициентами. Решение одной из таких задач представлено ниже.
Рассмотрим |
|
|
двустороннюю |
||
последовательность чисел Фибоначчи: |
|
||||
F |
, n , F |
0, F |
1,..., F |
F |
F |
n |
0 |
1 |
n 2 |
n 1 |
n |
…-21, 13, -8, 5, -3, 2, -1, 1, 0 ,1, 1, 2, 3, 5, 8, 13, 21… (1) |
|||||
и семейство скользящих многочленов степени |
n |
с |
|
||
коэффициентами из последовательности (1): |
|
|
~ |
|
|
~ |
|
|
~ |
|
|
~ |
|
|
|
|
n 1 |
( |
|
) |
(n m) |
n |
( |
|
) |
(n m) |
]} |
(4) |
||
... z( ) |
|
|
|
( ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, корни многочленов семейства
(2) являются решениями уравнений:
z |
|
z |
|
z |
n 2 |
|
|
... z |
n 1 |
|
|
|
|
|||||
|
n |
|
|
n 1 |
|
|
|
2 |
|
|
|
n |
|
|
||||
|
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
||
( |
|
) |
n m |
[z |
n |
z |
n 1 |
|
n 2 |
2 |
|
|||||||
|
|
|
|
|
( ) z |
|
( ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~
... z( ) n 1 ( ) n ]
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|
|
|
~ |
|
1 |
|
5 |
|
3 |
5 |
|
|
Так |
как |
|
|
|
|
|
1, |
то |
||||
|
1 |
|
5 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||
коэффициенты |
при |
степенях |
z |
|
в правой |
части |
||||||
|
|
|||||||||||
уравнения |
(5) |
стремятся |
к |
нулю |
при |
m . |
||||||
Отсюда, в силу непрерывной зависимости корней многочлена от его коэффициентов, немедленно следует, что корни уравнений (5) стремятся к корням многочлена:
F (z) z |
n |
z |
n 1 |
|
... z |
n 1 |
|
n |
(6) |
|
|
|
|
||||||
n |
|
|
|
|
|
|
|
|
|
и, следовательно, стремятся к корням уравнения |
|
||||||||
|
z |
n 1 |
|
n 1 |
0 , кроме z |
(7) |
|||
|
|
|
|||||||
P |
(z) F |
z |
n |
F |
z |
n 1 |
... F |
|
, m (2) |
||
|
|
|
|
||||||||
n m |
n m |
|
|
n m 1 |
|
|
|
|
2 n m |
|
|
|
Нас интересует предельное поведение корней |
||||||||||
многочленов (2) при m m |
. |
||||||||||
|
Рассмотрим |
сначала |
случай, |
|
когда m . |
||||||
Не ограничивая общности, будем сразу считать, что
m M n. Подставляя Fn m |
в форме Бинэ: |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n m) |
~ |
(n m) |
|
|
|
5 1 |
~ |
5 1 |
|
|||
|
|
|
|
|
|
|
|
||||||||
F |
|
|
[ |
|
( ) |
|
], |
|
|
|
|
|
, |
|
(3) |
n m |
|
5 |
|
|
|
|
|
2 |
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
в (2) получим следующую цепочку равенств:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
n |
|
|
(n m) |
|
|
~ |
(n m) |
|
|
|||||
Pn m |
(z) |
|
|
|
|
{z |
|
[ |
|
|
|
|
( ) |
|
|
|
] |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
n 1 |
[ |
(n m 1) |
|
|
~ |
|
(n m 1) |
] |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
||||||||||
... [ |
(2n m) |
|
|
|
|
~ |
|
(2n m) |
]} |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
(n m) {z n z n 1 z n 2 2 |
... z n 1 n |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
5 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
(n m) |
|
|
|
n 1 |
|
|
|
|
(n m) |
|
||||||||||
|
[z |
|
( |
) |
|
|
|
|
|
z |
|
|
|
( )( ) |
|
|
|
|
|||||||||||
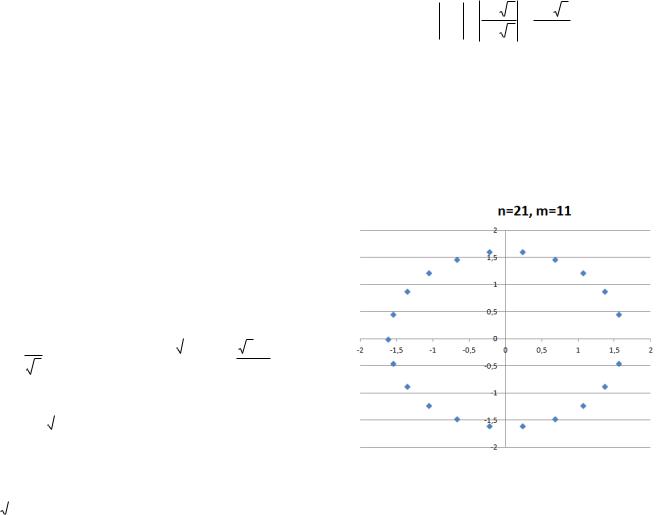
Рис. 1. Распределение корней при |
n 21, |
радиус окружности 1,618
Аналогичные рассуждения для уравнения (5), которое при m удобно представить в виде:
67
z |
|
z |
|
|
|
|
|
( ) z |
|
|
|
( ) |
|
... |
|||||||
|
n |
|
|
(n |
1) |
|
~ |
|
|
(n 2) |
|
~ |
2 |
|
|
||||||
z( ) |
|
|
|
( ) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
~ |
|
|
(n 1) |
|
|
|
~ |
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
(5') |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|||
( ~ ) |
( |
|
) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
[z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
] |
|
|||
|
z |
|
|
|
|
... z |
n 1 |
|
|
||||||||||||
|
|
n |
|
|
n 1 |
|
|
|
|
|
|
|
n |
|
|
||||||
показывают, |
|
|
что |
|
|
при |
|
m |
корни |
||||||||||||
многочленов из семейства (2) стремятся к корням уравнения:
z |
|
( ) |
|
0 |
, кроме z |
(8) |
|
n 1 |
~ |
n 1 |
|
~ |
|
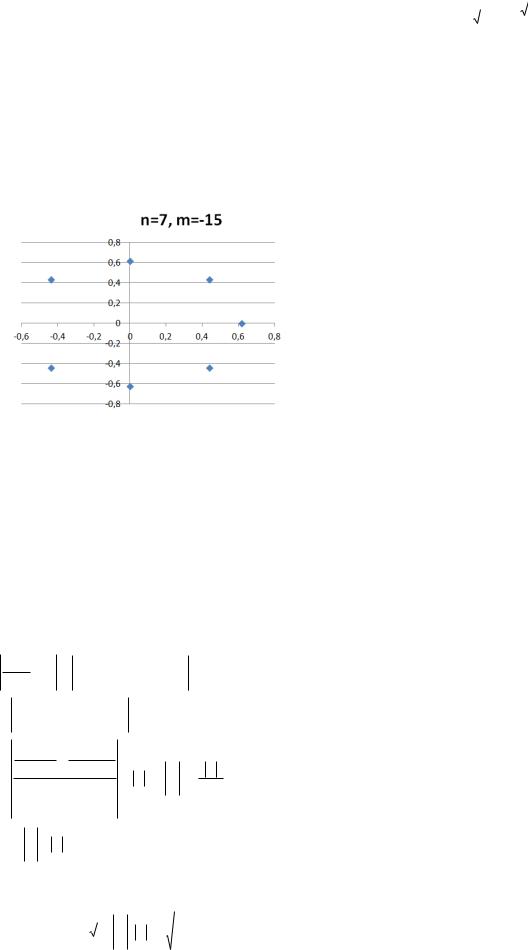
Понятно, также, что корни (8) отличаются от корней (7) только инверсией относительно единичной окружности. См. Рис.2.
Рис. 2. Распределение корней при n =7, радиус окружности 0,618
Интерес представляет также оценка разности корней (2) и (6) при увеличении m . Для получения такой оценки воспользуемся одним тонким неравенством Элснера [10]. Представим для этого
(2) в виде приведенного многочлена:
|
|
|
|
|
|
z |
|
n |
|
|
Fn m 1 |
z |
n 1 |
... |
F2n m |
|
0 |
|
(9) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Fn m |
|
|
|
|
|
Fn m |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И сравним корни (9) с корнями многочлена: |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
z |
|
|
|
... |
|
|
0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
(10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценим разность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
2n m |
|
|
|
~ |
|
2n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F |
|
|
|
|
|
|
|
|
|
|
|
|
n m |
|
|
|
|
|
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
~ |
|
n m |
|
|
|
|
|
~ |
2n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
( ) |
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
n m |
|
|
|
|
|
~ |
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
||||||||
|
() |
|
|
|
|
|
|
|
() |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n m |
|
|
|
2n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
() |
n |
|
|
|
|
|
() |
n m |
|
|
|
|
|
|
|
|
|
|
|
|
~ |
n |
|
|
|
~ |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
~ |
|
n m |
|
|
|
|
|
|
|
|
|
|
|
|
n m |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
~ n |
|
~ m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
при достаточно больших m . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Поэтому разность корней может быть оценена |
||||||||||||||||||||||||||||||||||||||||||
сверху величиной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
(2 ) |
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n (m) n |
|
2 |
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 1 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
) |
m |
|
|
|
|
|
|
5 |
|
|||
(3 |
5) n ( |
|
n |
(12) |
||||
|
2 |
|||||||
|
|
|
|
|
|
|
||
Иными словами, приближение к корням предельных многочленов имеет скорость убывающего слагаемого в представлении чисел Фибоначчи формулой Бинэ.
Понятно также, что в общем случае (необходимые определения см. например, в [3] и имеющимся там списке литературы), справедлива следующая
Теорема. Пусть числовая последовательность определяется линейным рекуррентным соотношением, удовлетворяющим свойству Пизо. Тогда корни скользящего вправо многочлена с убывающими степенями приближаются к вершинам правильного многоугольника, вписанного в окружность с радиусом равным наибольшему характеристическому числу данного рекуррентного соотношения.
Литература:
1.Метод многоугольных чисел в процедуре сглаживания временных рядов / Ю. А. Агранович, Н. В. Концевая, С. Л. Подвальный, В. Л. Хацкевич // Системы управления и информационные технологии. – 2009. - Вып.
4(38). - С.30-34
2.Агранович Ю.Я., Концевая Н.В., Хацкевич В.Л. Сглаживание временных рядов показателей финансовых рынков на основе многоугольных чисел // Прикладная эконометрика, №3(19), 2010, с.3-8.
3.Агранович Ю.Я., Концевая Н.В., Хацкевич В.Л. Метод многоугольных чисел в процедуре сглаживания временных рядов и приложения к исследованию финансовых рынков // Экономика и математические методы, т.46, 2010, вып.3, с.71-81.
4.Синтез статистического и детерминистского методов в проблеме сглаживания временных рядов / Ю. А. Агранович, Н. В. Концевая, С. Л. Подвальный, В. Л. Хацкевич // Системы управления и информационные технологии. – 2011. - №4 (46). - С. 4-7.
5.Скользящее усреднение на основе минимизации невязки в формуле Эйлера-Маклорена / Ю. А. Агранович, Н. В. Концевая, С. Л. Подвальный, В. Л. Хацкевич // Вестник Воронежского государственного технического университета. - 2011. - Т. 7. - № 12. - С. 4-6.
6.Агранович Ю.Я., Концевая Н.В. Метод определения параметров сглаживания временных рядов на основе минимизации невязки в формуле ЭйлераМаклорена // Современная экономика. Проблемы и решения, №7(18), 2011, с. 131-137.
7.Агранович Ю.Я., Концевая Н.В. Формула Эйлера-Маклорена в теории скользящего усреднения // Международный научно-исследовательский журнал, ч.1, 5(5), 2012, стр. 5-6.
8.Концевая, Н. В. Анализ методов заполнения пропусков во временных рядах показателей финансовых рынков / Н. В. Концевая // Вестник Воронежского государственного технического университета. – 2012. - Т.
8.- № 8. - С. 18-20.
9.Концевая, Н. В. Метод рандомизации заполнения пропусков во временных рядах при исследовании рыночных показателей / Н. В. Концевая // Системы управления и информационные технологии.
2012. - Т. 48. - № 2.2. - С. 259-263.
Elsner L. On the Variation of the Spectra of Matrices. // Linear Algebra and its Applications, 47: 127-138 (1982).
68
УДК 332.05
ПРЕОБРАЗОВАНИЯ СОВРЕМЕННОЙ РОССИЙСКОЙ ЭКОНОМИКИ: ТЕОРИЯ, ПРАКТИКА, ИННОВАЦИОННЫЕ ПЕРСПЕКТИВЫ
Студент группы МВ-101 Тараскова Елена Сергеевна Руководитель: д-р полит. наук, проф. Смышляев В.А.
В статье рассмотрены некоторые проблемы модернизации экономики России; выявлены специфика и противоречия политики преобразований в экономической сфере в РФ
Долгое время российская экономика функционировала за счѐт прежних достижений, созданных в эпоху СССР. Это относится, прежде всего, к индустриальной мощи, жилищнокоммунальной сфере, инфраструктуре, ядерному потенциалу страны, разведанным запасам нефти, газа и организации их добычи. Однако поддержка экстенсивного экономического роста не может продолжаться сколь угодно долго, поскольку активы изнашиваются, морально устаревают. Для дальнейшего развития экономика России нуждается в модернизации, причѐм модернизация должна сводиться к тому, чтобы Россия свернула с сырьевого пути развития. Также следует заметить, что приоритетные позиции, принадлежат инновациям, стратегия развития которых представлена в проекте "Инновационная Россия - 2020", который определяет направления развития и характер инновационной политики в Российской Федерации на период до 2020 года в соответствии с ранее представленной «Концепцией долгосрочного социальноэкономического развития Российской Федерации на период до 2020 года».
Модернизацию экономики России следует понимать, как процесс преобразований, с целью обновления экономики, соответствия еѐ вызовам современности, а также занятия конкурентоспособных позиций (прежде всего в инновационнотехнологической сфере), а также еѐ способности динамично функционировать и развиваться в режиме перманентного прогресса [2].
Стоит отметить, что модернизация экономики России – предельно сложная проблема. Несмотря на имеющийся высокий потенциал к занятию лидирующих позиций в мировой экономике, существует ряд проблем, которые ощутимо затрудняют этот процесс: сохранение экспортносырьевой модели национальной экономики; низкий (с тенденцией к дальнейшему снижению) уровень еѐ конкурентоспособности; существенная зависимость российской экономики от внешнеэкономической конъюнктуры, а также от кризисных явлений в мировой финансово-банковской системе; многолетняя практика принятия дискриминационных мер; недобросовестной конкуренции в отношении России; недостаточно действенный (плотный) и рачительный государственный контроль над национальными (и прежде всего природными) ресурсами; наличие тенденции к ухудшению состояния (в том числе в виде «изношенности») материально-технической базы национальной экономики и сырьевой базы промышленности и энергетики; неравномерное
(«диспропорциональное», «асинхронное») развитие регионов (субъектов РФ); прогрессирующая трудонедостаточность, самым тесным образом связанная с продолжающей ухудшаться демографической ситуацией в нашей стране; слабая устойчивость и защищѐнность национальной финансовой системы; сохранение условий для коррупции и криминализации хозяйственнофинансовых отношений; тенденция к эскалации незаконной миграции, деструктивно влияющей на качественный состав трудовых ресурсов, задействованных в национальной экономике; замедление темпов экономического роста, возникновение дефицита торгового и платѐжного баланса; сокращение доходных статей федерального бюджета, способное спровоцировать дальнейшее секвестирование финансовой поддержки социальной сферы жизнедеятельности и развития РФ, что с неизбежностью повлияет на качество и уровень жизни социального большинства в нашей стране; вероятность дефицита в средне- и долгосрочной перспективе (особенно в отдельных регионах Российской Федерации) топливно-энергетических, водных и биологических ресурсов, в совокупности способного «сбить» темпы экономического роста в нашей стране
[1].
Заметим, что для современной российской экономики характерна чрезмерная и не по всем аспектам эффективная роль государства, доминирующего над бизнесом. Причина низкого уровня жизни и расслоения общества в России - потребительское отношение государства к бизнесу. Причем стоит отметить, что преимущественные позиции и поддержку государства имеет крупный бизнес. Из вышесказанного следует, что пока государство не начнет уходить из экономики, в России не удастся прекратить поляризацию общества.
Перейдем к проблеме инновационного развития экономики Российской Федерации. И вновь начнем рассмотрение вопроса со значения данного термина. Основной преградой, стоящей на пути инновационного развития России, является исторически сложившаяся катастрофическая нехватка предприимчивых лидеров инноваций, способных не только генерировать инновационные идеи, но и, что самое главное, быстро превращать их в успешный инновационный бизнес или продукт.
На сегодняшний день существует стратегия инновационного развития Российской Федерации на период до 2020 года «Инновационная Россия – 2020», в которой четко поставлены цели и приоритеты государственной инновационной политики. Данная
69
