
Дифракционные решетки в антеннах СВЧ и КВЧ диапазонов волн. Юдин В.И., Пастернак Ю.Г
.pdf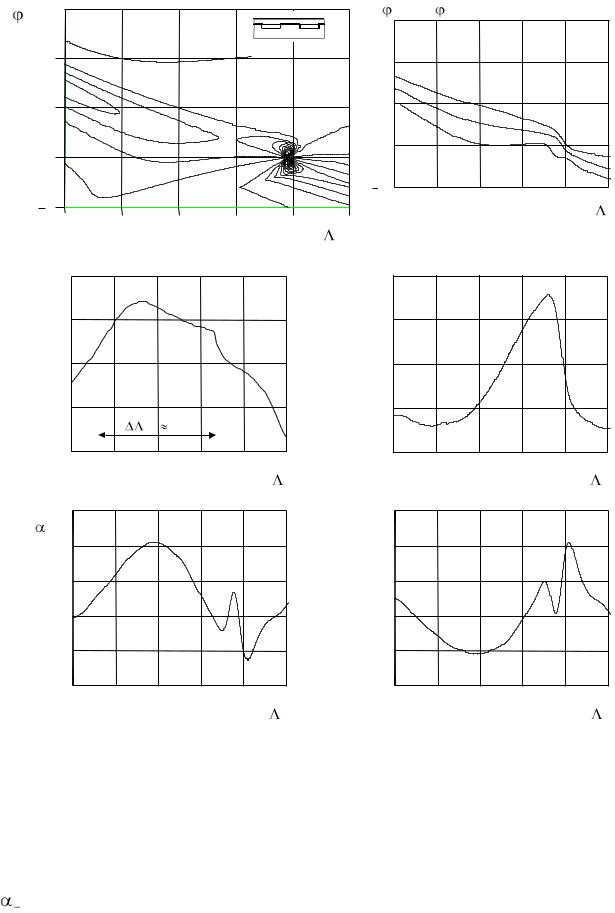
,град |
|
|
|
|
|
|
|
( -1) 0.7,( -1)max,град |
|
|
|||
20 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|A-1| |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
10 |
|
|
|
|
|
|
|
|
|
|
б) |
|
|
0.75 |
0.8 |
|
0.85 |
|
0.9 |
0.95 |
1 |
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
0.98 |
|
|
|
|
|
|A-1| |
|
|
|
|
|
|
|
vф/v0 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
0.96 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0.94 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0.92 |
|
|
|
|
|
|
|
|
% |
15 % |
|
|
|
|
|
|
|
|
|
0 |
0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
0.9 0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
|
|
|
|
|
в) |
|
|
|
|
|
|
г) |
|
|
0.5 |
|
|
|
|
|
|
|
Эфф,% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.42 |
|
|
|
|
|
|
|
68 |
|
|
|
|
|
0.34 |
|
|
|
|
|
|
|
56 |
|
|
|
|
|
0.26 |
|
|
|
|
|
|
|
44 |
|
|
|
|
|
0.18 |
|
|
|
|
|
|
|
32 |
|
|
|
|
|
0.1 0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
20 0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
||
|
|
|
|
д) |
|
|
|
|
|
|
е) |
|
|
Рис. 3.17. Дисперсионные характеристики однопазовой металлической гребенки |
|
||||||||||||
|
с диэлектрическим слоем при нулевой величине зазора между ними |
|
|
||||||||||
Однако использование на практике такого режима весьма ограничено. Это связано с наличием асимметричного (экспоненциально убывающего) амплитудного распределения поля по длине реальной (конечной) ПАДТ, характеризующейся значительной величиной постоянной вытекания. Рис. 3.17, д показывает частотную зависимость постоянной вытекания поверхностной волны
1 , отнесенной к одному периоду структуры, (т. е. постоянной ослабления в амплитудном распределении поля в направлении движения волны) для

рассматриваемой ПАДТ. В полосе = 0.8 0.9 ее величина колеблется от 0.31 до 0.43, что соответствует общей эффективности структуры (длиной около 15 L ) в (31 43) % (рис. 3.17, е). Малая эффективность обусловлена низким значением КИП. Нецелесообразным будет и применение неоднородной связи ПДВ с гребенкой (например, за счет клиновидного прицельного зазора: c const > 0) для выравнивания распределения поля вдоль координаты x, поскольку угол наклона ПДВ к гребенке должен иметь значительную величину, а с ростом прицельного расстояния УЧХ заметно трансформируется.
Поиск геометрии ПАДТ, обеспечивающей ослабление углочастотной
дисперсии |
поверхностных волн (при ненулевом прицельном |
параметре ПДВ: |
c = const > |
0), следует вести среди более сложных структур |
прямоугольного |
профиля. Компьютерные эксперименты показывают, что введение внутри периода (паза) гребенки нескольких дополнительных разномерных «колодцев» может приводить к существенной трансформации УЧХ, в частности, к расширению области пониженной углочастотной чувствительности.
Рассмотрим характеристики ПАДТ, раскрыв решетки которой (плоскость, проведенная по краям ребер, разделяющих пазы) имеет два несовпадающих уровня: внутрипериодный ( z  b
b 2) и межпериодный ( z b
2) и межпериодный ( z b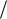 2 ), рис. 2.11. На периоде
2 ), рис. 2.11. На периоде
рассматриваемой дифракционной решетки размещено в общем случае N разноразмерных «колодцев». При незначительном разносе частот глубинных резонансов смежных «колодцев» связь их электромагнитных полей приведет к ослабленной дисперсии на межрезонансном участке.
На рис. 3.18 приведены результаты моделирования ПАДТ с двухуровневой гребенкой, характеризующейся следующими параметрами: t = 2.5, b = h =1,
t =0.25 L , c = 0.3 L , b = 0.2 L , N = 3, l1 = l3 = 0.4 L , h1 = h3 = 0, l2 = 0.2 L , h2 = 0.15 L .
В ее УЧХ можно четко выделить зону с ослабленной дисперсией поверхностной волны ( = 0.9 0.96, = 0.5 4 : рис. 3.18, а). Угло-частотная чувствительность в указанном частотном диапазоне (
4 : рис. 3.18, а). Угло-частотная чувствительность в указанном частотном диапазоне (  5 % относительно 0 = 0.93) составляет величину порядка = 0.55
5 % относительно 0 = 0.93) составляет величину порядка = 0.55  % (рис. 3.18, б). При фиксированном направлении прихода волны
% (рис. 3.18, б). При фиксированном направлении прихода волны  2.5
2.5 ее преобразование в (-1)-ю ПГ осуществляется
ее преобразование в (-1)-ю ПГ осуществляется
в полосе  6.5 % (рис. 3.18, в) с высокой эффективностью: (50 80) % (рис. 3.18, д). Последняя обусловлена тем, что постоянная вытекания в данной зоне обладает значениями (рис. 3.18, г), близкими к оптимальным (для структуры длиной 15 L
6.5 % (рис. 3.18, в) с высокой эффективностью: (50 80) % (рис. 3.18, д). Последняя обусловлена тем, что постоянная вытекания в данной зоне обладает значениями (рис. 3.18, г), близкими к оптимальным (для структуры длиной 15 L
Эmax 80 % при |
1 опт 0.067 0.104). Из рис. 3.18, б, г видно, что частотные |
области резонансного поведения постоянной вытекания (–1)-й ПГ и стабилизации пространственного положения главного лепестка ДН исследуемой структуры совпадают.
Кривая 3.18, б подтверждает закономерность, общую для всех дифракционных периодических структур: области, характеризующиеся небольшой величиной крутизны угло-частотной дисперсии, соответствуют участкам расширения главного лепестка ДН. Данный факт позволяет сформулировать следующую рекомендацию по методике проектирования ПАДТ с расширенной полосой рабочих частот, в которой сохраняется фиксированная угловая ориентация
|
|
|
|
|
|
|
|
( |
-1) 0.7,( |
-1)max,град |
|
|
||
,град |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|A-1| |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
10 0.85 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.88 |
0.91 |
0.94 |
0.97 |
1 |
||
10 |
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.85 |
0.88 |
0.91 |
0.94 |
|
0.97 |
1 |
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
0.15 |
|
|
|
|
|
|
|A-1| |
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
4.5 |
|
|
|
|
|
|
|
0.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.09 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.06 |
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
0.03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
% |
6.5% |
|
|
|
|
|
|
|
|
|
|
0 |
0.85 |
0.88 |
0.91 |
0.94 |
0.97 |
|
1 |
0 |
0.85 |
0.88 |
0.91 |
0.94 |
0.97 |
1 |
|
|
|
в) |
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
Эфф,% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0.85 |
0.88 |
0.91 |
0.94 |
0.97 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
д) |
|
|
|
|
|
|
|
|
Рис. 3.18. Результаты компьютерного моделирования ПАДТ |
|
|
||||||||||
|
|
с двухуровневой гребенкой, накрытой слоем диэлектрика |
|
|
||||||||||
максимума их диаграммы направленности: для достижения максимальной эффективности подобных антенн целесообразно синтезировать их в виде совокупности синфазно запитанных подрешеток, содержащих не более 5-8 периодов каждая. Математическое моделирование амплитудного распределения подобных подрешеток показывает, что оно является близким к оптимальному.
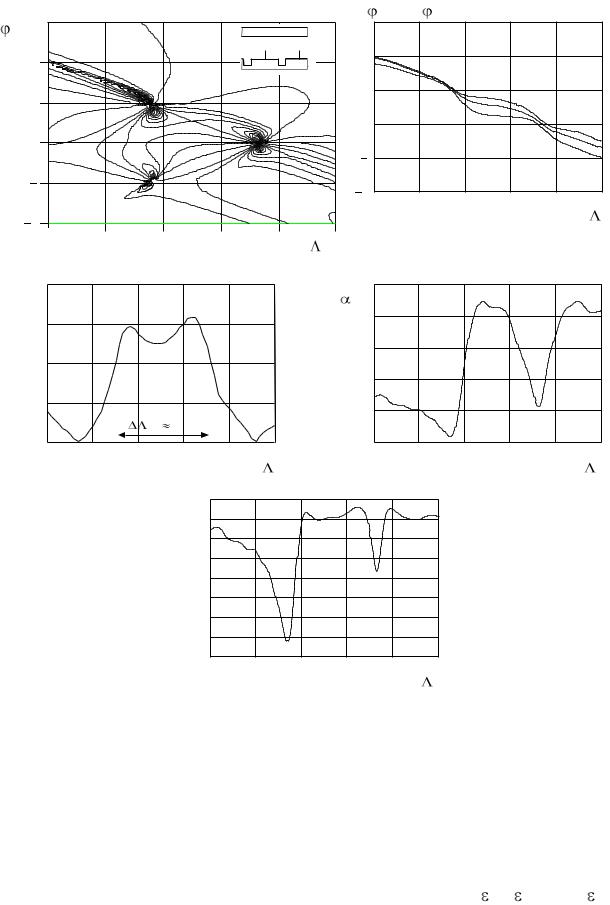
На рис. 3.19 показаны результаты численного моделирования ПАДТ на основе двухуровневой гребенки с двумя колодцами в пазу: t = b = 2.5, h =1,
t = 0.2 L , c = 0.3 L , b = 0.15 L , N = 3, li = 0.333 L , h1 = 0, h2 = 0.125 L , h3 = 0.25 L . Как

видно, исследуемая структура обладает двумя зонами снижения углочастотной
чувствительности: = 0.81 |
0.88 и = 0.94 0.97, |
где |
равны соответственно |
0.3 и 0.1 %. Наиболее |
интересным участком |
УЧХ |
является первая из |
выделенных зон, поскольку в ней частотная стабилизация сектора
максимального приема |
1 |
0.7 |
сохраняется в полосе 9 % (рис. 3.19, |
б, в). |
||
|
|
|
|
|
||
Наличие в отмеченных зонах пониженной крутизны зависимости |
1 |
0.7 |
от |
|||
|
|
|
|
|
||
свидетельствует о действительном ослаблении дисперсии ПГ в двухуровневой структуре и появлении признаков аномальной дисперсии. При отклонении прицельного расстояния относительно исходного на ( 15) % (рис. 3.19, в: штрих  c = 0.25 L , сплошная 0.3 L , штрих-пунктир 0.35 L ) интенсивность поверхностной волны несущественно изменяется, что позволяет использовать на практике неоднородную связь ПДВ с решеткой для обеспечения более высокой эффективности ПАДТ. Выбор степени клиновидности зазора осуществляется по
c = 0.25 L , сплошная 0.3 L , штрих-пунктир 0.35 L ) интенсивность поверхностной волны несущественно изменяется, что позволяет использовать на практике неоднородную связь ПДВ с решеткой для обеспечения более высокой эффективности ПАДТ. Выбор степени клиновидности зазора осуществляется по
расчетной зависимости постоянной вытекания |
1 |
от прицельного параметра ПДВ. |
||
|
|
|
|
|
На рис. 3.19 г приведена частотная зависимость постоянной |
1 |
для с= 0.3 L , из |
||
|
|
|
|
|
которой видно, что в рассматриваемой полосе (по |
) постоянная вытекания имеет |
|||
величину порядка 0.2 0.3. При этом расчетная эффективность ПАДТ (при длине структуры 15 L и однородной связи ПДВ с гребенкой) составляет (45 60) %. Расширение полосы частот, в пределах которой наблюдается ослабление дисперсии ПГ, в общем случае приводит к снижению эффективности преобразования, поддерживать которую на заданном уровне приходится с помощью дополнительных мер: введением клиновидной связи слоя диэлектрика и гребенки.
Таким образом, ПАДТ на основе металлодиэлектрических двухуровневых гребенок, обладая повышенным числом степеней свободы по управлению углочастотными характеристиками в заданной области параметров первичной волны, позволяют реализовать режим эффективного преобразования волн, не
свойственный простым структурам: в пределах (7 9) |
%-й полосы частот |
||
стабилизировать угловой сектор максимального приема |
1 |
0.7 |
в направлении |
|
|
||
прихода волны.
Приведенная в главе 2 математическая модель дифракции плоских однородных линейно-поляризованных волн на двухуровневых гребенках с диэлектрическим слоем (рис. 2.11) позволяет учесть конечную ширину ребер, разделяющих пазы ДР. Актуальность использования структуры, подобной показанной на рис. 2.11, в качестве излучающей апертуры дифракционных плоских антенн СВЧ диапазона обусловлена возможностью расширения полосы аномальной дисперсии (–1)-й ПГ планарного диэлектрического волновода за счет наложения друг на друга внутрипазовых резонансов путем выбора их геометрических размеров и перспективой создания плоских дифракционных антенн на основе одномерно-периодичных структур, которые эффективно осуществляют взаимное преобразование объемных и поверхностных волн как Е-, так и Н-поляризаций (в режимах приема и передачи сигналов). Значительный интерес вызывает также сравнение
,град |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|A-1| |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
0.75 |
0.8 |
|
0.85 |
|
0.9 |
0.95 |
1 |
|
|
|
|
|
|
а) |
|
|
|
6 |
|
|
|
|
|
|
|
|
|A-1| |
|
|
|
|
|
|
|
|
4.5 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
|
% |
8.5% |
|
|
|
|
0 |
0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
|
|
|
|
|
|
в) |
|
|
|
|
( -1) 0.7,( -1)max,град |
|
|
||||
20 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
10 0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
|
|
|
|
|
б) |
|
|
0.4 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
0.32 |
|
|
|
|
|
|
0.24 |
|
|
|
|
|
|
0.16 |
|
|
|
|
|
|
0.08 |
|
|
|
|
|
|
0 |
0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
|
|
|
|
г) |
|
|
Рис. 3.19. Дисперсионные характеристики двухуровневой гребенки со сложной внутрипериодной структурой, накрытой слоем диэлектрика
основных антенных характеристик металлических двухуровневых гребенок и ДР типа «эшелетт».
Ниже приведены результаты компьютерного моделирования дифракционной структуры со следующими параметрами: диэлектрическая проницаемость
материала ПДВ |
t |
2.56 , толщина последнего составляет t 0.25L , |
|
|
|
относительная ширина двухуровневого паза выбрана равной 0.834L |
||
( l1 l3 0.292L, l2 |
0.25L ), глубины колодцев - h1 h3 0 , величина h 2 |
|
изменяет свое значение от 0.1 до 0.25 периода L .
Прицельное расстояние c изменялось в ходе численного моделирования в пределах от 0.15 до 0.6 периода L . Диапазон изменения глубины паза верхнего уровня b составлял (0.1 0.25) L . Частотный параметр задачи
дифракции |
L |
0 |
варьировался от 0.62 до 1.02. Поляризация падающей |
|
|
|
волны во всех рассмотренных случаях – Н (в силу запредельности колодца 2 для падающих Е-поляризованных волн свойства данной двухуровневой ДР и одноуровневой однопазовой гребенки, в которую переходит первая из них при h2 0 , практически совпадают).

Обращает на себя внимание тот факт, что на всех приведенных ниже в данном подразделе картах линий одинакового уровня УЧХ для двухуровневой гребенки с диэлектрическим слоем имеется несколько резонансных областей (в отличие от простой однопазовой гребенки, накрытой диэлектриком. Каждая из них соответствует внутрипазовым колебаниям гребенки и пространственному резонансу Брэгга второго порядка, наблюдающегося при синфазном сложении отраженных от каждого паза волн.
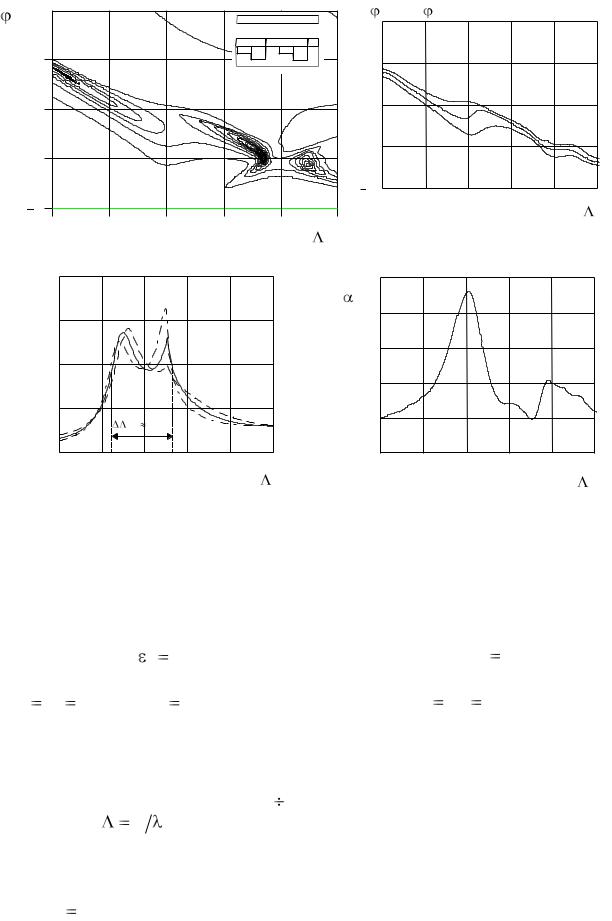
На рис. 3.20 приведены основные дисперсионные и энергетические характеристики исследуемой структуры, характеризующейся параметрами
b 0.1L, h2 0.25L , c 0.15L . На УЧХ (рис. 3.20, а) четко видны |
|
|
резонансы, проявляющиеся при значениях частотного параметра |
1 |
0.845, |
|
|
2 |
0.925 . В данном интервале частот существенно ослаблена угло- |
|
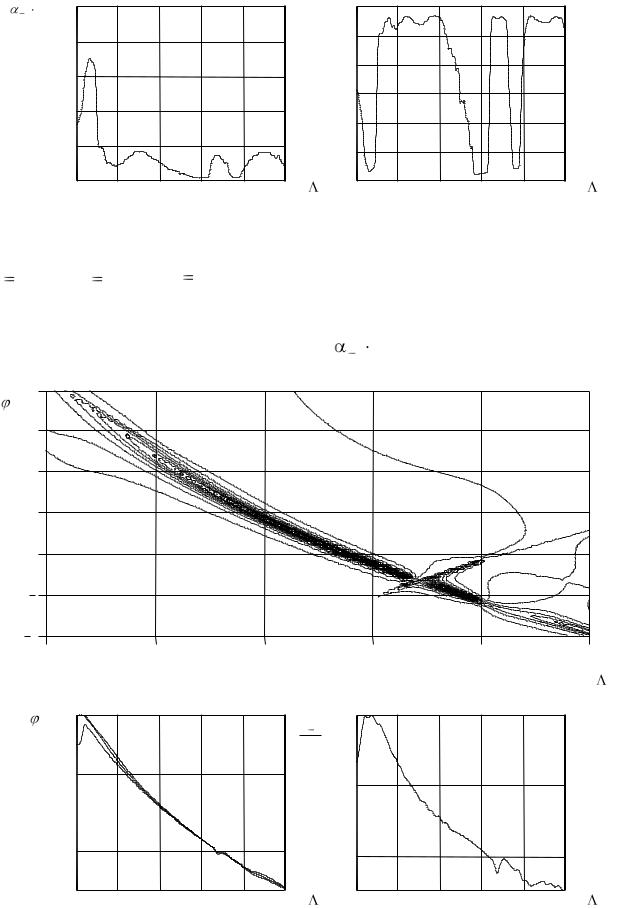
частотная дисперсия главного лепестка ДН структуры, рис. 3.20, б. Причиной этого явления служит аномальная дисперсия фазовой скорости (–1)-й ПГ Флоке планарного диэлектрического волновода внутри вышеупомянутого участка изменения величины , рис. 3.20,в . Участки угловой стабилизации главного лепестка ДН при изменении частоты падающей волны (рис. 3.20, б) связаны с интервалами возрастания фазовой скорости (–1)-й ПГ, где имеет место аномальная дисперсия (рис. 3.20, в).
Из рис. 3.20,б,г следует, что столообразные участки УЧХ соответствуют интервалам «всплесков» постоянной вытекания, что может приводить к уменьшению эффективности антенной структуры конечной длины вследствие уменьшения ее КИП, рис. 3.20, е. Это явление следует учитывать при построении ПАДТ СВЧ и КВЧ диапазонов волн: противоречащие друг другу требования угловой стабилизации в широкой полосе частот главного лепестка ДН и высокой эффективности ПАДТ требуют применения алгоритмов оптимизации.
Резкие изменения постоянной вытекания вблизи значений частотного параметра 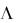 0.7 и 0.96 вызваны внутрипазовыми резонансами, а ее «всплеск» около точки 0.87 обусловлен брэгговским резонансом второго порядка, рис. 3.20, г. Эквивалентная схема ПАДТ, работающей в режиме резонанса Брэгга 2-го порядка, может быть представлена в виде режекторного фильтра, причем аномальная дисперсия (–1)-й ПГ наблюдается в области частот, соответствующей области высокочастотной фильтрации.
0.7 и 0.96 вызваны внутрипазовыми резонансами, а ее «всплеск» около точки 0.87 обусловлен брэгговским резонансом второго порядка, рис. 3.20, г. Эквивалентная схема ПАДТ, работающей в режиме резонанса Брэгга 2-го порядка, может быть представлена в виде режекторного фильтра, причем аномальная дисперсия (–1)-й ПГ наблюдается в области частот, соответствующей области высокочастотной фильтрации.
Таким образом, для стабилизации углового положения главного лепестка ДН в полосе частот прототипом ПАДТ должен быть фильтр высокой частоты. Данное условие справедливо для ДР любой конструкции. В случае использования гребенок различной конфигурации оно означает, что сопротивление, вносимое в ПДВ пазами гребенки, должно иметь емкостный характер. Разнос по частоте брэгговского резонанса второго порядка и внутрипазовых резонансов можно использовать для расширения частотной

полосы угловой стабилизации главного лепестка ДН плоской дифракционной антенны.
При увеличении прицельного расстояния до c 0.3L (рис. 3.21) вследствие ослабления степени связи между полем (–1)-й поверхностной гармоникой Флоке ПДВ и колебаниями в пазах ДР уменьшается величина модуля вносимого пазами гребенки реактивного сопротивления в поверхностный импеданс планарного диэлектрического волновода, что заметным образом сказывается на дисперсионные характеристики структуры: вдвое уменьшается протяженность зоны стабилизации углового положения главного лепестка (в единицах частотного параметра), рис. 3.21,а,б; в исследуемой полосе частот не наблюдается явление срыва поверхностной
волны в |
объемную (рис. 3.21,в), |
подобное |
иллюстрируемому рис. 3.20,в |
(диапазон |
изменения частотного |
параметра |
0.86...0.89 , в котором |
вычисленное значение фазовой скорости (–1)-й ПГ, нормированное к скорости света в вакууме, превышает единицу). Следует отметить, что подобные значения фазовой скорости типичны для закрытых металлических волноводных структур. Описанные в главе 2 учебного пособия математические модели позволяет определить участки частот, соответствующие срыву поверхностных волн, и тем самым устранить сопутствующие этому явления резких «скачков» главного лепестка ДН ПАДТ.
По сравнению со случаем, соответствующим рис. 3.20, значительно уменьшается средняя величина постоянной вытекания в исследуемой полосе частот (рис. 3.21,г); частотные зависимости постоянной вытекания –1-й ПГ диэлектрического волновода и эффективности ПАДТ (рис. 3.21,е) становятся менее изрезанными вследствие увеличения добротности глубинных резонансов в пазах гребенки из-за уменьшения процессов энергетического обмена между ПДВ и ДР. Адекватность описанной выше модели подтверждается и тем, что частотные участки, на которых увеличивается величина постоянной вытекания, сопровождаются расширением главного лепестка ДН исследуемой структуры
(рис. 3.20,б,г; 3.21,б,г).
Рис. 3.22, 3.23 подтверждают монотонный характер уменьшения величины постоянной вытекания при увеличении прицельного расстояния. Данный факт очень важен для физической реализуемости разрабатываемых плоских дифракционных антенн с энергетическими характеристиками, близкими к оптимальным. Дело в том, что колебательная частотная зависимость постоянной вытекания может привести к соответствующему характеру изменения прицельного расстояния вдоль излучающей апертуры, что чревато либо физической нереализуемостью электродинамического объекта, либо низкой технологичностью проектируемого изделия (вследствие его сложной геометрической конфигурации и электрических свойств).
Возрастающие участки угло-частотной характеристики исследуемой структуры уменьшают свою протяженность по мере увеличения параметра c структуры: ширина соответствующего частотного диапазона изменяется от 0.12 относительных единиц (рис. 3.21,а – прицельное расстояние c 0.3L ) до 0.55
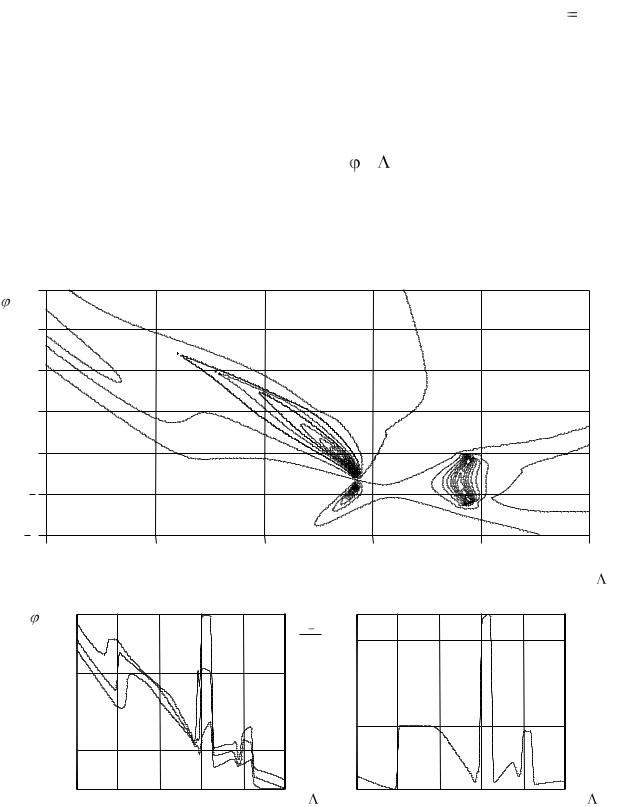
относительных единиц 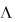 (рис. 3.23,а – прицельное расстояние c 0.6L ). Соответственно монотонно уменьшается и ширина частотно-независимых участков главного лепестка ДН структуры вплоть до полного их исчезновения
(рис. 3.23,а – прицельное расстояние c 0.6L ). Соответственно монотонно уменьшается и ширина частотно-независимых участков главного лепестка ДН структуры вплоть до полного их исчезновения
(рис. 3.23,б).
Большой практической значимостью обладает тот факт, что почти во всем исследуемом интервале частот при двукратном изменении величины прицельного расстояния (случаях, соответствующих рис. 3.21-3.23) среднее положение максимума ДН на плоскости ( , ) изменяется незначительно.
Следовательно, даже в ПАДТ, имеющих существенную длину, не будет происходить раздвоение главного лепестка диаграммы направленности при амплитудном распределении в их раскрыве, близком к равномерному, как обеспечивающему максимальную величину эффективности антенного устройства.
,0 |
20 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
|
|
|
|
|
|
а) |
|
|
|
|
|
,0 |
|
|
|
|
|
v 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
|
|
|
б) |
|
|
|
|
|
в) |
|
|
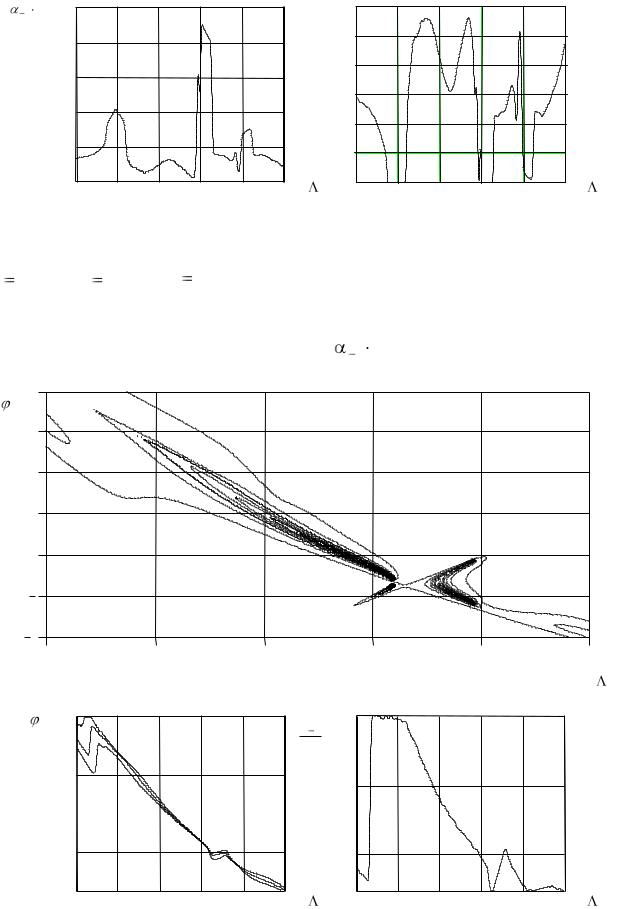
|
1 L |
1.5 |
|
|
|
|
|
Э,% |
8 5 |
|
|
|
|
|
|
|
1.2 |
|
|
|
|
|
|
7 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 5 |
|
|
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 5 |
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 5 |
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 5 |
0 .7 |
0 .78 |
0 .86 |
0 .94 |
1 .02 |
|
|
0.62 |
0.7 |
|
0.78 |
0.86 |
0.94 |
1.02 |
0 .62 |
|||||
|
|
|
|
|
|
г) |
|
|
|
|
|
д) |
|
|
Рис. 3.20. Характеристики двухуровневой гребенки со слоем диэлектрика при |
||||||||||||||
b |
0.1L, |
h2 |
0.25L , c |
0.15L : а) УЧХ; |
б) частотная зависимость углового |
|||||||||
положения главного лепестка ДН (по уровню –3 дБ); в) нормированная фазовая |
||||||||||||||
скорость (–1)-й ПГ; г) частотная зависимость постоянной вытекания, |
||||||||||||||
нормированной |
к |
периоду |
структуры |
1 L ; д) частотная зависимость |
||||||||||
эффективности ПАДТ, содержащей 18 периодов L |
|
|
|
|
||||||||||
|
,0 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.62 |
|
|
|
0.7 |
|
|
0.78 |
0.86 |
|
|
0.94 |
|
1.02 |
|
|
|
|
|
|
а) |
|
|
|
|
|
|
, |
0 |
|
|
|
|
v |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.95 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0.9 |
|
|
|
|
|
|
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
|
|
|
|
б) |
|
|
|
|
|
в) |
|
|
|
1 |
L |
0.6 |
|
|
|
|
|
Э,% |
85 |
|
|
|
|
|
|
|
0.48 |
|
|
|
|
|
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
0.36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
0.24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
0.12 |
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
0.62 |
0.7 |
|
0.78 |
0.86 |
0.94 |
1.02 |
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
|
|
|
|
|
|
|
г) |
|
|
|
|
|
д) |
|
|
Рис. 3.21. Характеристики двухуровневой гребенки со слоем диэлектрика при |
|||||||||||||||
b |
0.1L, |
h2 |
0.25L , c |
0.3L : а) УЧХ; |
б) частотная зависимость углового |
||||||||||
положения главного лепестка ДН (по уровню –3 дБ); в) нормированная фазовая |
|||||||||||||||
скорость (–1)-й ПГ; г) частотная зависимость постоянной вытекания, |
|||||||||||||||
нормированной |
к |
периоду |
структуры |
1 L ; д) частотная зависимость |
|||||||||||
эффективности ПАДТ, содержащей 18 периодов L |
|
|
|
|
|||||||||||
|
,0 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.62 |
|
|
|
0.7 |
|
|
0.78 |
0.86 |
|
|
0.94 |
|
1.02 |
|
|
|
|
|
|
а) |
|
|
|
|
|
,0 |
|
|
|
|
|
v 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c0 |
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.95 |
|
|
|
|
|
0 |
|
|
|
|
|
0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
0.62 |
0.7 |
0.78 |
0.86 |
0.94 |
1.02 |
|
|
|
б) |
|
|
|
|
|
в) |
|
|
