
Обыкновенные дифференциальные уравнения с приложениями к математическим моделям специальных дисциплин. Бырдин А.П., Сидоренко А.А
.pdf
3. В симметрической форме уравнения с разделяющимися переменными имеют вид:
|
P (x)Q ( y)dx |
P (x)Q ( y)dy |
0. |
(2.10) |
||||||||||
|
1 |
1 |
|
|
2 |
|
|
2 |
|
|
|
|||
|
Разделение переменных в этом уравнении осуществляется |
|||||||||||||
умножением обеих частей (2.10) на множитель |
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
P2 (x)Q1( y) |
|
|
|||||||
Общий интеграл уравнения имеет вид: |
|
|
||||||||||||
|
|
|
P (x) |
|
Q |
2 |
( y) |
|
|
|||||
|
|
|
|
1 |
|
dx |
|
|
|
|
dy C. |
|
(2.11) |
|
|
|
|
P2 (x) |
|
Q1( y) |
|
||||||||
|
При получении общего интеграла, как и ранее, |
|||||||||||||
предполагалось, |
что |
в рассматриваемом |
прямоугольнике |
|||||||||||
a |
x b , c y |
d функции P2 (x) и Q1( y) |
не обращаются в |
|||||||||||
ноль. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если P2 ( ) |
0 , |
где |
(a,b) , Q1( ) |
0 , где |
(c, d) , |
||||||||
то, |
кроме общего интеграла, |
уравнение имеет решения |
y |
|||||||||||
и x |
, не получаемые из общего решения. Соответствующие |
|||||||||||||
этим решениям интегральные кривые – прямые, параллельные
осям координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Частный интеграл, удовлетворяющий начальному |
|||||||||||||||||||||||||||
условию y(x0 ) |
|
y0 , записывается в виде: |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x P (x) |
|
y Q |
2 |
( y) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
dx |
|
|
|
|
dy |
0. |
|
|
|
|
(2.12) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 (x) |
|
|
Q1( y) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Задачи для самостоятельного решения |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
y |
1 |
y 2 . Ответ: y |
sin(x |
|
c), |
|
x |
c |
|
|
и |
y 1. |
||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||
2. |
y |
|
|
y 2 |
2 y |
|
. |
Ответ: |
|
y |
|
2 |
|
, |
|
|
|
C |
|
и |
y |
0 . |
|||||||
|
|
|
|
2x |
|
1 Cx |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
y sin |
x |
dx |
cos |
x |
dy |
0. |
Ответ: |
y |
|
C |
. |
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
cos x |
|
|
|
|
|
||||||
20

4. |
x(1 y2 )dx y(1 x2 )dy 0 . |
|
|
|
|
|
|
|
|||
|
|
|
|
Ответ:1 |
y2 |
C(1 |
x2 ), |
0 |
C |
. |
|
|
|
|
|
|
|
1 |
|
C)2 ; |
|
|
|
5. |
|
y sin xdx dy 0. |
Ответ: y |
(cosx |
y |
0. |
|
||||
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
2.2. Однородные дифференциальные уравнения первого порядка
1. К уравнениям с разделяющимися переменными приводятся однородные уравнения после выполнения замены неизвестной функции на новую функцию.
Определение. Однородным дифференциальным уравнением 1-го порядка называется уравнение вида
y |
y |
. |
(2.13) |
|
|||
|
x |
|
|
Таким образом, уравнение (2.1) будет являться |
|||
однородным дифференциальным уравнением, если |
функция |
||
f (x, y) представляет собой однородную функцию переменных
x и y нулевой степени однородности f (tx,ty) t 0 f (x, y) . В
этом случае функция зависит лишь от отношения этих переменных.
Теорема 2. Однородное дифференциальное уравнение (2.13) при условии, что функция (u) непрерывна и (u) u в
интервале u (a,b) , имеет общий интеграл, выражаемый в квадратурах. При этом через каждую точку M 0 (x0 , y0 )
области плоскости, лежащей внутри вертикальных углов, ограниченных прямыми y ax и y bx и не содержащей
прямой x 0 , проходит единственная интегральная кривая.
Доказательство. Выполнив подстановку
u |
y |
(2.14) |
|
|
|||
x |
|||
|
|
относительно новой функции u(x) получим дифференциальное уравнение с разделяющимися переменными. Действительно,
21

так как y xu , то y |
u xu . Подставляя в уравнение (2.13), |
|||||||
получим |
|
|
|
|
|
|
|
|
|
x |
du |
|
(u) |
|
u . |
(2.15) |
|
|
dx |
|
||||||
|
|
|
|
|
|
|
|
|
Предполагая, что |
(u) |
u и x |
|
0 , разделяем переменные |
||||
и интегрируем: |
|
|
|
|
|
|
|
|
|
du |
|
|
dx |
C. |
|
||
|
|
|
|
|
|
|
|
|
|
(u) |
u |
x |
|
||||
|
|
|
||||||
Обозначив интеграл в левой части последнего равенства через Ф(u) , где u  xy , получим общий интеграл уравнения
xy , получим общий интеграл уравнения
(2.13) в виде:
|
y |
|
|
(2.16) |
||
Ф |
ln |
x |
C. |
|||
x |
||||||
|
|
|
|
|
||
На основе теоремы об уравнениях с разделяющимися переменными (теорема 1, п.2.1) можем утверждать, что если в
рассматриваемом интервале |
(a,b) |
функция |
(u) |
u |
||
непрерывна |
(для чего достаточно непрерывности |
функции |
||||
(u) ) и не |
обращается в ноль, |
то |
в области такой, |
что |
||
a u b , x |
0 уравнение |
(2.15) |
имеет общий |
интеграл, |
||
выражаемый в квадратурах, а через каждую точку (x0 , u0 ) указанной области проходит единственная интегральная
кривая. |
Это же утверждение справедливо для уравнения (2.13), |
|||||||||||||||
из которого уравнение (2.15) получается подстановкой. |
||||||||||||||||
Соответствующее значение параметра C получается из |
||||||||||||||||
(2.16): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C0 |
Ф |
|
y0 |
|
ln |
|
x0 |
|
. |
|
|
|||
|
|
|
|
|
|
|
||||||||||
|
|
|
x0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким |
образом, |
решение |
с начальными условиями |
|||||||||||||
y(x0 ) |
y0 |
будет иметь вид |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ф |
y |
Ф |
|
y0 |
ln |
x |
. |
|||||||
|
|
x |
|
x0 |
x0 |
|
||||||||||
22

Разрешив частный интеграл относительно функции y(x) , получим частное решение
y |
xФ |
1 |
Ф |
y0 |
ln |
x |
, |
(2.17) |
|||
|
x0 |
x0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
где Ф 1 - обратная функция для Ф(u) . |
|
|
|
|
|||||||
Область единственности решения задачи Коши a |
|
y |
b |
||||||||
|
|
||||||||||
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
или ax y bx , |
x |
0 , представляет собой внутреннюю часть |
|||||||||
двух вертикальных |
углов, |
ограниченных прямыми |
y ax , |
||||||||
y bx , причем берутся те два угла, которые не содержат ось
OY , т.к. x |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Пример. |
|
|
Найти |
|
частный |
|
интеграл |
|
|
уравнения |
|||||||||||||||||
y |
|
x |
y |
|
|
0 , удовлетворяющее начальному условию y(0) |
1. |
||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
x |
2y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Решение. |
Применяем |
подстановку y |
ux . Получим |
|
|||||||||||||||||||||||
|
|
|
x |
du |
u |
|
1 |
u |
|
0 ; |
|
x |
du |
|
2u 2 |
2u |
1 |
0 ; |
|
||||||||||
|
|
|
dx |
1 |
2u |
|
dx |
|
2u |
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
2u 1 |
|
|
du |
|
dx |
|
0 |
; |
1 |
|
|
|
ln C , |
||||||||||||||
|
|
|
|
|
|
2u 2 2u 1 |
|
||||||||||||||||||||||
|
|
|
|
|
ln |
ln |
x |
||||||||||||||||||||||
|
2u 2 |
|
2u |
1 |
|
x |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
С 0 , x2 (2u 2 |
|
2u 1) C 2 ; x2 |
|
|
2xy 2y2 |
C |
, C C 2 |
0 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
||
Таким образом, получен общий интеграл рассматриваемого ОДУ. Для получения частного решения подставим в общий интеграл начальные данные y(0) 1.
Определим постоянную C1 : C1 |
2 . Частный |
интеграл, |
|
удовлетворяющий заданным начальным данным, имеет вид |
|||
x2 2xy 2y2 |
2 . |
|
|
2. Если |
в дифференциальном |
уравнении xu |
(u) u |
(2.15), вытекающим из однородного уравнения (2.13), найдутся такие значения u , при которых уравнение (u) u имеет
23

решения, то каждому такому |
u0 |
будет отвечать решение |
||||||||||||||||||||||||||||||||||||||||||||||||
дифференциального |
уравнения |
|
|
y |
|
|
u0 , |
т.е. |
|
y |
|
u0 x , |
не |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вытекающее из общего интеграла. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Пример. |
Решить уравнение xy |
|
|
x2 |
|
|
|
y 2 |
|
|
|
y . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Решение. |
Перепишем уравнение в виде y |
|
|
|
y |
|
|
1 |
|
y 2 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
x 2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и положим |
y |
xu , |
откуда |
y |
xu |
|
u . |
|
Подставляя в |
|||||||||||||||||||||||||||||||||||||||||
уравнение выражения |
|
y |
и y , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
dx |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
u 2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 u |
2 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Последнее |
получим |
|
при |
|
|
условии |
|
x |
1 |
u2 |
0 . |
||||||||||||||||||||||||||||||||||||
Интегрированием |
находим |
|
arcsinu |
|
|
ln |
x |
|
|
lnC1 , |
C1 |
0 ; |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
arcsinu |
ln C1 |
x |
. |
Учитывая, |
что |
С1 |
х |
|
|
|
С1х |
|
и |
|
обозначая |
|||||||||||||||||||||||||||||||||||
С1 |
|
С, |
получим |
arcsinu |
|
lnCx , |
где |
|
|
|
|
ln Cx |
|
|
|
|
|
|
или |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
e 2 |
|
Cx |
e 2 . |
Заменяя |
u |
на |
|
получим общий интеграл |
||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
arcsin |
y |
|
ln(Cx). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
Положим теперь x 0 и |
1 |
|
|
|
u 2 |
0 . |
Но |
|
x |
0 |
не |
||||||||||||||||||||||||||||||||||||
удовлетворяет |
уравнению |
при |
произвольном |
у. Из |
второго |
|||||||||||||||||||||||||||||||||||||||||||||
равенства имеем 1 |
|
у 2 |
|
0 , у |
|
|
|
х |
. Проверка показывает, что |
|||||||||||||||||||||||||||||||||||||||||
|
х2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
эти функции являются решениями уравнения.
3.Однородное дифференциальное уравнение 1-го порядка
всимметрической форме имеет вид
P(x, y)dx Q(x, y)dy 0, |
(2.18) |
24

где P(x, y) и Q(x, y) - однородные функции, одной и той же степени однородности:
P(tx,ty) |
t n P(x, y) , |
Q(tx,ty) |
t nQ(x, y) . |
(2.19) |
|||||||||
Если в определении однородных функций в качестве |
|||||||||||||
параметра |
взять |
|
t |
x 1 , |
то |
получим |
более |
наглядные |
|||||
соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ~ |
y |
, |
|
|
|
n ~ |
|
y |
. |
(2.20) |
P(x, y) |
x |
P |
|
Q(x, y) |
x |
Q |
|
|
|||||
x |
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Число |
n в |
равенствах |
(2.19) |
или |
(2.20) |
называется |
|||||||
степенью (или порядком) однородности. |
|
|
|
|
|
||||||||
Например, |
функция |
z |
2x 3y - |
|
однородная 1-го |
||||||||
порядка, z |
x2 |
3xy 4y2 - однородная функция 2-ой степени |
|||||||||||
однородности.
Симметрическая форма дифференциального уравнения имеет то преимущество перед уравнением вида (2.1), что в качестве искомой функции можно выбирать либо y(x) , либо
x( y) , в зависимости от удобства.
Однородное дифференциальное уравнение (2.18)-(2.19) сводится к уравнению с разделяющимися переменными подстановкой
y |
ux , |
dy |
udx |
xdu, |
(2.21) |
или подстановкой |
|
|
|
|
|
x |
uy , |
dx |
udy |
ydu . |
(2.22) |
Построим общий интеграл однородного уравнения, записанного в симметрической форме. Сделаем замену искомой функции y по формуле (2.21). Будем иметь
P(x,ux)dx Q(x,ux)(udx xdu) 0 .
Поскольку
P(x, y) xn P 1, |
y |
; |
Q(x, y) |
xnQ 1, |
y |
, |
|
x |
x |
||||||
|
|
|
|
|
то, подставляя y ux , имеем
25

xn P(1,u)dx xnQ(1,u)(udx xdu) |
0 |
или |
|
P(1,u) uQ(1,u) dx xQ(1,u)du 0, |
(2.23) |
x 0. |
(2.24) |
Уравнение (2.23) является дифференциальным уравнением с разделяющимися переменными. Разделяя переменные, получаем:
|
dx |
|
|
Q(1, u)du |
0, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
P(1, u) uQ(1, u) |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
P(1, u) uQ(1, u) 0, |
|
|
|
|
|
|
|||||||
|
x |
0. |
|
|
|
|
|
|
|
|
||||
Интегрируя (2.25), находим: |
|
|
|
|
|
|
||||||||
|
ln |
|
x |
|
|
Q(1,u)du |
|
ln |
|
C1 |
|
, |
||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
P(1,u) uQ(1,u) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получим общее решение |
||||||||||||||
выражающее x как функцию от u : |
|
|
|
|
|
|||||||||
(2.25)
(2.26)
C1 0.
уравнения (2.25),
x C exp |
Q(1,u)du |
, (C |
|
C1 |
|
). |
||
|
|
|||||||
|
|
|
|
|||||
P(1,u) |
uQ(1,u) |
|||||||
|
|
|
|
|
|
|||
Введя обозначение
Q(1,u)du
(u) P(1,u) uQ(1,u),
и заменяя u  xy , получим общий интеграл уравнения (2.18) в
xy , получим общий интеграл уравнения (2.18) в
виде:
|
y |
|
|
|
|
|
|
x Ce |
x . |
(2.27) |
|
Разделяя переменные в уравнении (2.23) мы потеряли |
|||
решения вида u u0 , где u0 |
- корень |
уравнения (2.26). |
|
Подставляя эти значения в формулу (2.21) найдем, что
26

|
y u0 x x |
0 |
(2.28) |
являются |
решениями |
однородного |
уравнения, |
соответствующие интегральные кривые – полупрямые, примыкающие к началу координат. Эти решения могут входить в совокупность, определяемую общим интегралом уравнения, но могут быть и особыми решениями. Особыми решениями могут быть также полуоси оси OY : x 0 ( y 0) . Других
особых решений это уравнение иметь не может.
Пример. Найти решения дифференциального уравнения
x y cos |
y |
dx |
x cos |
y |
dy 0. . |
|
|
||||
|
x |
|
|
x |
|
Решение. Это уравнение является однородным, т.к. коэффициентами при dx и dy являются функции одной степени однородности:
|
tx ty cos |
ty |
t |
|
x |
y cos |
y |
; |
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
tx |
|
|
|
|
|
|
|
|
x |
|
||||
|
tx cos |
ty |
|
t |
x cos |
y |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
tx |
|
|
|
|
|
|
x |
|
|
|
|||||
Введем замену y |
xu . Имеем |
|
|
|
|
|
|
|
|
|
||||||||||
(x xucosu)dx |
|
|
x cosu(xdu |
udx) |
0, |
|||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
cosudu |
0. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Интегрируя, |
получим: |
|
|
ln |
x |
|
|
sinu |
C. |
Таким образом, |
||||||||||
общий интеграл уравнения имеет вид: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||||
|
|
ln |
x |
|
|
|
sin |
C. |
|
|
|
|||||||||
|
|
|
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4*. Рассмотрим геометрическое свойство интегральных кривых однородного уравнения.
Поле направлений, определяемое однородным дифференциальным уравнением 1-го порядка, а следовательно, и интегральные кривые этого уравнения обладают одним интересным свойством. Запишем однородное уравнение в виде
27

|
y |
y |
, |
(2.13) |
|
|
|
||||
|
|
x |
|
|
|
и отметим, |
что функция |
( y x) сохраняет |
постоянное |
||
значение во |
всех точках любой полупрямой y |
kx (x |
0) , |
||
выходящей из начала координат, если, конечно, функция |
(k) |
||||
существует при данном значении k . Поэтому все такие лучи являются изоклинами уравнения (2.13).
Выберем какую-нибудь интегральную кривую, не совпадающую с такими лучами. Если увеличить или уменьшить радиусы-векторы во всех точках интегральной кривой в одно и то же число раз, то получим кривую, у которой направление касательных во всех точках будет таким же, что и в соответствующих точках взятой первоначально интегральной кривой. Поэтому полученные таким образом линии будут также являться интегральными кривыми уравнения.
Указанное преобразование радиусов-векторов называется
преобразованием подобия с центром подобия в начале координат. Оно означает замену текущих координат (x, y)
линии текущими координатами (X ,Y ) новой линии по формулам
X kx, |
Y ky. |
(2.29) |
Таким образом, однородное дифференциальное уравнение 1-го порядка обладает следующим свойством: всякая кривая,
полученная из интегральной кривой однородного уравнения преобразованием подобия с центром подобия в начале координат, тоже является интегральной кривой.
Верно и обратное утверждение: все интегральные кривые,
входящие в общий интеграл
 y
y 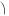
x Ce  x
x  ,
,
и не являющиеся лучами, выходящими из начала координат, могут быть получены при помощи преобразования подобия
(2.29) из одной такой интегральной кривой.
28

Из приведенного свойства интегральных кривых однородного уравнения следует:
1) если интегральная кривая, отличная от луча,
выходящего из точки (0,0) и, |
следовательно, заключенная на |
|
некотором интервале изменения x |
между двумя полупрямыми |
|
y uk x (k 1,2) , примыкает |
к |
точке (0,0) , то и все |
интегральные кривые, заключенные между этими лучами, примыкают к точке (0,0) ;
2) если некоторая линия является интегральной кривой, то и симметричная относительно (0,0) линия является
интегральной кривой; 3) если одна из интегральных кривых замкнута, то и все
интегральные кривые замкнуты.
5. Рассмотрим физическую задачу, приводящую к однородному дифференциальному уравнению: найти форму зеркала, собирающего параллельные лучи в одну точку.
Выберем за ось OX прямую, параллельную лучам, за начало координат – точку пересечения всех лучей после отражения и проведем сечение поверхности зеркала плоскостью XOY . На этой плоскости будем искать кривую, обладающую указанным свойством (рис. 5).
Из геометрической оптики известно, что для идеальной зеркальной поверхности (что мы и предполагаем) углы падения
и отражения равны: |
. Поэтому |
треугольник |
ОТМ |
||||||
равнобедренный, следовательно TO |
OM . |
Если |
точка M |
||||||
|
|
|
|
|
|
||||
имеет координаты x, y , то OM |
x2 |
y 2 . Координата точки |
|||||||
T находится из уравнения касательной |
|
|
|
|
|
|
|
||
|
Y y y (X |
x) , |
|
|
|
|
|
|
|
где X ,Y - текущие |
координаты. |
Полагая Y |
0 , |
X |
OT , |
||||
получим: |
|
|
|
|
|
|
|
|
|
y y (OT x) , OT x |
|
x |
. |
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
y |
|
|
|
|
29
