
Учебное пособие 2049
.pdf
приведенном выражении есть число, как того и требует понятие функционала. Для первой вариации получим
F ( )d 0 I S.
I|S есть вариация величины скачка потенциала на S. Так
как эта величина неизвестна, то I 0. Перепишем F, используя формулу Грина
F |
|
2 d |
|
|
d |
|
|
d |
|
|
d 0 |
I |
|
. |
|
|
|||||||||||||||
|
|
|
|||||||||||||
|
|
n |
|
n |
n |
|
|
|
S |
||||||
|
|
S |
|
S |
|
|
|
|
|
|
|
|
|||
Здесь S+ и S– – разные стороны линии (поверхности) разреза, а Г – остальная часть границы (не включающая разрез). Очевидно, что направления вектора нормали к поверхностям S+ и S– противоположны, тем самым
|
|
d |
|
d |
|
( |
|
S |
|
|
S )d |
|||||||||
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||
S |
n |
S |
|
n |
|
|
S |
n |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
( |
|
S |
|
|
S )d |
|
Id . |
|||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
|
n |
||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
S |
||||||
Вариация I = const на S, так как скачок потенциала I постоянен в каждой точке поверхности S. Таким образом,
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
F d |
|
d |
|
0 |
|
|
d |
|
I |
|
S . |
||
n |
|
n |
|
|
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
S |
|
|
|
|
|
||
Итак, для того, чтобы функционал F достигал экстремума, необходимо:
2 0 |
в области , |
(2.10) |
|||||
|
|
0 |
на поверхности Г, |
(2.11) |
|||
|
|
||||||
|
n |
|
|
|
|
||
|
S |
|
d 0 |
(2.12) |
|||
|
|||||||
|
|
n |
|
|
|||
41

(знак «+» или «–» определяется выбором направления нормали n к поверхности S). С учетом фиксации в любой точке области задачи , получили требуемую краевую задачу, описывающую трехмерное распределение поля.
В более общей формулировке может ставиться дополнительно k интегральных условий типа (2.12). В этом случае определяется k непересекающихся поверхностей разрез, на каждой из которых задается свой поток Ф0i , а величины скачков потенциала Ii
|
S |
Ii , i=1, …, k, |
|
|
i |
определяются путем решения вариационной задачи. Функционал такой задачи примет вид
k
F( , I1, I2,..., Ik ) 12 ( )2d 0iIi Si ,
i 1
для которого также можно показать, что его минимальное значение соответствует распределению поля, удовлетворяющего уравнениям (2.10), (2.11) и естественным условиям
n d 0i , i=1,…, k.
Si
В случае конечно-элементной реализации получим дополнительно к узловым переменным k степеней свободы: I1, … , Ik.
Рассмотрим особенности учета условия сохранения потока градиентов (2.9) в реализации МКЭ. Как известно, стандартная конечно-элементная процедура состоит в вычислении матричных элементов и вектора правых частей для каждого конечного элемента (т. н. локальной системы линейных уравнений) и добавлении их в глобальную систему, относящуюся ко всей конечно-элементной сетке. Отметим, что в рассматриваемой формулировке поверхность разреза S является внутренней по отношению к и тем самым должна находиться внутри конечно-элементной сетки, но при этом она не может проходить по внутренней части элементов, а может проходить
42
только по границам элемен- |
– |
|
+ |
||||
|
|||||||
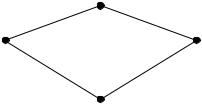
тов. Возьмем два двумерных |
|
||||||
конечных элемента, примы- |
1 |
|
|
||||
кающих к поверхности S с |
|
|
2 |
||||
разных |
сторон, |
как показано 4 |
|
|
|||
на рис. 2.3. |
условия |
(2.12) |
|
|
|
||
Если бы |
|
|
|
||||
не было (в функционале (2.9) |
3 |
|
|
||||
нет второго слагаемого), то |
|
|
|||||
локальные системы этих эле- |
|
|
S |
||||
|
|
||||||
ментов имели вид |
|
Рис. 2.3 |
|||||
Sii(e) i |
Sij(e) j |
Sik(e) k |
0, |
||||
|
|
|
|||||
Sij(e) i |
S(jje) j |
S(jke) k |
0, |
|
|
|
|
Sik(e) i S(jke) j Skk(e) k |
0, |
|
|
|
|||
где S(e) – матрица жесткости элемента с номером e; индексы i, j, k совпадают с глобальными номерами узлов элемента e. Глобальная система уравнений, соответствующая этим элементам, выглядит так:
S11(1) |
S11(2) 1 |
S12(1) 2 |
S13(1) |
S13(2) |
3 |
S14(2) 4 |
0, |
|||||
|
S(1) |
|
S(1) |
|
2 |
|
S |
(1) |
|
3 |
|
0, |
|
12 |
1 |
22 |
|
|
|
23 |
|
|
|
||
S13(1) |
S13(2) 1 |
S23(1) 2 |
S33(1) |
S33(2) |
3 |
S34(2) 4 |
0, |
|||||
|
S14(2) |
1 |
|
|
|
|
S34(2) 3 |
S44(2) 4 |
0. |
|||
Если S является поверхностью разреза с условием (2.12), то в узлах 1 и 3 значения справа и слева не равны друг другу, а связаны соотношением
1+ – 1– = I, |
3+ – 3– = I. |
Так что по одной узловой переменной можно исключить, например, 1+ и 3+. Чтобы правильно построить глобальную систему, запишем выражения для элементных функционалов
43
F(1) |
|
1 |
|
S(1)( |
|
|
I)2 |
|
1 |
S(1) |
2 |
1 |
S(1) |
( |
|
I)2 |
|
||||||||||||
|
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
2 11 |
1 |
|
|
|
|
|
2 |
|
22 |
2 |
|
33 |
|
3 |
|
|
||||||||||||
|
S12(1) ( 1 I) 2 S13(1) ( 1 I)( 3 |
I) S23(1)( 3 I) 2, |
|||||||||||||||||||||||||||
F(2) |
|
1 |
S(2) 2 |
|
|
1 |
S(2) |
2 |
|
1 |
S(2) 2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2 11 |
1 |
|
2 |
|
33 |
|
|
3 |
|
|
2 44 |
|
4 |
|
|
|
|
|||||||||||
|
S(2) |
|
3 |
S(2) |
|
4 |
S(2) |
3 |
|
. |
|
|
|
||||||||||||||||
|
|
|
13 1 |
|
14 |
|
1 |
|
|
|
34 |
|
4 |
|
|
|
|
||||||||||||
Заметим, что каждому узлу на S соответствует только одна независимая переменная – та, что вычисляется по левую сторону. Но при этом появилась дополнительная переменная, которая ставится в соответствие не узлам, а всему разрезу в целом
– сила тока I. Суммарный функционал представится в виде
F = F(1) + F(2) + Ф0I.
Минимизируя F по переменным 1– , 2 , 3– , 4 и I, получим систему
F |
|
S11(1) |
S11(2) |
1 S12(1) 2 |
S13(1) |
S13(2) 3 |
|||||||||||||
1 |
|||||||||||||||||||
|
|
|
|
S11(1) |
|
|
|
|
I 0, |
|
|
|
|
||||||
|
|
|
S14(2) 4 |
|
S13(1) |
|
|
|
|
||||||||||
F |
|
S(1) |
|
|
S(1) |
2 |
S(1) |
3 |
S |
(1) |
S(1) I 0, |
||||||||
|
|
|
|
|
|||||||||||||||
2 |
12 |
1 |
|
22 |
|
|
|
23 |
|
12 |
23 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
|
S13(1) |
S13(2) |
1 |
S23(1) 2 |
(S33(1) |
S33(2) ) 3 |
||||||||||||
3 |
|
||||||||||||||||||
|
|
|
|
S13(1) |
|
|
|
|
I 0, |
|
|
|
|||||||
|
|
|
S34(2) 4 |
S33(1) |
|
|
|
||||||||||||
F |
|
S(2) |
1 |
S(2) |
3 |
S(2) |
4 |
0, |
|
||||||||||
|
|
|
|
||||||||||||||||
4 |
14 |
|
|
34 |
|
|
|
44 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F |
S11(1) S13(1) 1 |
S12(1) S23(1) |
2 |
|
|||||||||||||||
|
|
||||||||||||||||||
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S13(1) S33(1) 3 S11(1) S33(1) 2S13(1) I 0.
44
С точки зрения программной реализации МКЭ важно иметь правило формирования этой системы из локальных систем. Поэтому приведем локальную систему для первого и второго элемента соответственно:
S11(1) 1 S12(1) 2 S13(1) 3 S11(1) S13(1) I 0,
S12(1) 1 S22(1) 2 S23(1) 3 S12(1) S23(1) I 0,
S13(1) 1 S23(1) 2 S33(1) 3 S13(1) S33(1) I 0,
S11(1) S13(1) 1 S12(1) S23(1) 2 S13(1) S33(1) 3
S11(1) S33(1) 2S13(1) I 0
и
S11(2) 1 S13(2) 3 S14(2) 4 0,
S13(2) 1 S33(2) 3 S34(2) 4 0,
S14(2) 1 S34(2) 3 S44(2) 4 0.
Как видно, появление дополнительного условия сохранения потока меняет локальные системы конечных элементов, примыкающих к поверхности разреза только с одной стороны, а элементы по другую сторону от S дают такой же вклад, как если бы условия не было.
Поскольку все дискретные уравнения получены из соотношений, накладывающие ограничения только на разность потенциалов, а не на сам потенциал, то для исключения неоднозначности МКЭ-решения необходимо зафиксировать одну из узловых величин (например, принять 2 0).
2.3. Учет условия постоянства потенциала и потока его градиента на внутренних границах
области решения краевой задачи
В постановке ряда краевых задач для уравнения Лапласа встречается дополнительное условие постоянства значений потенциала:
= const
на некоторой внутренней границе многосвязной области. 45

Ввиду того, что это условие ставится для самого потенциала (а не производных), оно имеет внешнее сходство с краевым условием Дирихле. Тем не менее, оно существенно отличается от последнего, так как требует лишь равенства граничных значений функции, но не определяет эти значения. Другими словами, на данной границе потенциал сохраняет неизменное значение, которое заранее неизвестно и должно определиться в результате решения краевой задачи.
Данное условие допускает вариационную формулировку, которая наиболее удобна при конечно-элементной реализации решения. Действительно, взяв первую вариацию функционала, соответствующего уравнению Лапласа,
F( ) |
1 |
( )2 d |
(2.13) |
|
|||
2 |
|
|
|
и применив формулу Грина, получим
F |
2 d |
|
d . |
|
|||
|
|
n |
|
Пусть на части границы Г, например Г1, задано условие= const. Будем рассматривать вариацию функционала по всем функциям, удовлетворяющим этому условию. Тогда = const на Г1 и тем самым
F |
2 d |
|
d |
|
d |
n |
|
||||
|
|
* |
n |
||
|
1 |
|
|
|
|
(здесь Г* – остальная часть границы: Г = Г1 + Г*).
Таким образом, для того, чтобы достигался минимум функционала (2.13), что соответствует F = 0, необходимо
2 0 |
в области , |
(2.14) |
0 на Г* (естественное граничное условие), (2.15)
n
46
|
|
d 0. |
(2.16) |
|
|||
|
n |
|
|
1 |
|
|
|
Последнее равенство имеет вид интегрального условия. Его левую часть можно интерпретировать поток градиента потенциала через поверхность Г1. Таким образом, функция, доставляющая экстремум функционалу и принимающая постоянное значение на Г1, будет автоматически удовлетворять уравнению Лапласа (2.14), однородному граничному условию Неймана (2.15) и интегральному условию (2.16).
В более общей формулировке интегральное условие имеет вид
|
|
dS Q. |
(2.17) |
|
|||
|
n |
|
|
1 |
|
|
|
При этом одновременно должно выполняться условие на
Г1:
= const.
Вновь рассмотрим функционал запасенной энергии скалярного поля (2.13). Добавим к нему слагаемое, равное произведению заданного значения Q потока через поверхность Г1 и самого потенциала на этой поверхности:
|
|
F( ) |
1 |
( )2 d Q |
|
1 . |
|
(2.18) |
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для первой вариации имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||
F ( )d Q |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 d |
|
|
d Q |
|
1 |
|
|
|
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
* n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
d Q |
|
. |
||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
* n |
1 |
|
|
|
|||||||||||||
47

Здесь изменен знак перед поверхностным интегралом по Г1, так как нормаль n – внешняя по отношению к области – заменена на внутреннюю нормаль n .
Таким образом, если функционал (2.18) рассматривать на множестве всех функций достаточной степени гладкости, заранее принимающих постоянное значение на Г1, то функция, доставляющая минимум этому функционалу, будет удовлетворять на уравнению Лапласа
= 0,
на Г* – естественному граничному условию
0,n
и интегральному соотношению
|
|
d Q. |
(2.17 ) |
|
|||
|
n |
|
|
1 |
|
|
|
Очевидно, что функционал (2.17) соответствует более общему случаю; рассмотренная выше вариационная формулировка на основе (2.13) может быть получена из (2.17) при Q = 0. Также отметим, что данная формулировка не исключает условия Дирихле, играющего, к слову, как и условие = const, роль главного краевого условия. Более того, оно является необходимым при численной реализации для исключения неоднозначности решения (все уравнения и соотношения накладываются на разность потенциала).
Итак, найден вариационный принцип, который учитывает интегральное соотношение (2.17 ) для заданного значения заряда как необходимое условие экстремума. Рассмотренная формулировка обобщается на случай задачи с k аналогичными дополнительными ограничениями. В такой системе определяются k поверхностей i, на каждой из которых задается своё значение потока градиента Qi. Функционал такой задачи примет вид
k
F( ) 12 ( )2d Qi i .
i 1
48

Его минимальное значение, определяемое на множестве функций, сохраняющих постоянные значения на соответствующих границах 1i, т.е.
1i const , i = 1, … , k,
соответствует распределению поля, удовлетворяющему уравнению Лапласа =0, однородному граничному условию Неймана 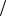 n 0 и условиям фиксации зарядов
n 0 и условиям фиксации зарядов
d Qi , i = 1,…, k.
1i n
Из методов численного решения краевых задач, имеющих вариационную формулировку, наиболее эффективным является метод конечных элементов. Рассмотрим особенности применения МКЭ к решению краевой задачи для уравнения Лапласа с учетом дополнительных условий типа постоянства потенциала и интегрального соотношения в виде фиксированного потока его градиента.
Сначала обратим внимание на то, что в терминах МКЭ условие = const на границе Г1 означает, что во всех узлах ко- нечно-элементной сетки, лежащих на Г1, потенциал должен быть одинаков. Например, для фрагмента сетки, изображенного на рис. 2.4, данное условие приводит к тому, что узловые величины 1-го, 3-го и 5-го узлов равны друг другу:
1 = 3 = 5. (2.19)
Действительно, внутри конечного элемента e искомая функция (e) аппроксимируется суммой
(e) iNi(e) , |
(2.20) |
i |
|
где i – узловые переменные, {Ni(e) } – базисные функции
(функции формы) элемента, причем каждая из этих функций Ni(e) в узле с номером i равна единице, а во всех остальных – нулю, а также в любой точке элемента выполняется соотноше-
49
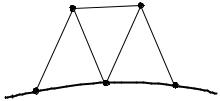
ние i Ni(e) 1. Поэтому на части границы Г1, к которой при-
мыкает элемент e, функция будет определяться суммой (2.20), в которой останутся только слагаемые, соответствующие узлам на Г1, что с учетом равенства (2.19) обеспечит постоянство функции. К примеру, для элементов 1 и 3 на рис. 2.4 получим
(1)(x,y) 1N1(1) 3N3(1) 1(N1(1) N3(1)) 1 const,
(3)(x,y) 3N3(3) 5N5(3) 1(N3(3) N5(3)) 1 const.
2 4
1 |
3 |
5 |
Г1 |
Рис. 2.4. Фрагмент конечно-элементной сетки из трех элементов
Первый шаг любой конечно-элементной процедуры – разбиение расчетной области на конечные элементы, которое производится без пропусков и перекрытий. Отметим, что хотя в рассматриваемой формулировке поверхность Г1 может находиться внутри области (правда, при этом величина Q в соотношении (2.17) должна непременно равняться нулю), на практике она, как правило, является внешней по отношению ки тем самым должна проходить по границе конечноэлементной сетки. Именно этот случай внешней границы Г1 будет подразумеваться в дальнейших рассуждениях. В любом случае триангуляция области должна быть выполнена так, чтобы элементы, примыкающие к Г1, имели в пересечении с Г1 точку или сторону в двумерном случае, точку, либо ребро, либо грань – в трехмерном.
50
